第3回 AVL木で木構造を学ぼう
はやしつとむ
アナハイムテクノロジー株式会社
2009/4/13
オブジェクト指向によって、アルゴリズムは隠ぺいされていることが多くなった。しかし、「用意されていない処理」が求められたときに対応できるだろうか(編集部)
第2回「単純なキューと循環キュー」では、循環キュー構造を実装したCyclicQueueの解説と、TListやLinkedListを利用したキューについての比較を行いました。
今回は、木構造を取り上げます。引き続き筆者はDelphi 2009でサンプルプログラムを作成していますが、Delphiをお持ちでない方は下記のURLからTurboDelphiをダウンロードしてぜひインストールして見て下さい。
| 関連リンク: | |
| Delphiトライアル版/無償バージョン http://www.codegear.com/jp/downloads/free/delphi |
|
 木構造とは何か?
木構造とは何か?
木構造は、データの関係を根(ROOT)から複数の枝(EDGE)をたどって節点(NODE)を経由しながら葉(LEAF)へと至るようなデータ構造です。また、各ノードをルートに見立てて、それ以下の木構造を部分木と呼びます。
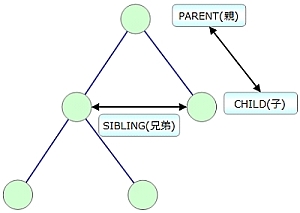
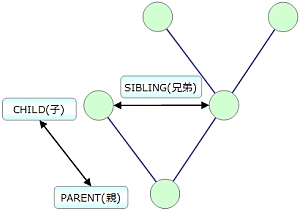
どうして根が一番上なんだというのはいつも思う疑問ですが、逆さまに書くと見辛いかもしれません。試しに逆さまの木構造の図を作ってみました。
他方、NODE間の上下関係は親(PARENT)と子(CHILD)と呼ばれますし、高さ(深さ?)が同じ位置にある節点同士は兄弟(SIBLING)と呼ばれて、この辺は家系図の呼称が使われています。こちらの方は、上から下へたどるのが普通だし、考え方としても分かりやすいですね。
思いつきですが、いっそのこと根から葉へ向かうのではなくて、単子葉植物の「ひげ根(MUSTACHE)」のように根が枝分かれしながら地中へ向かっていると考えた方がいいかもしれません。つまり、木構造ではなくて根構造ですね。まあ、冗談ですが。
 木構造をたどる
木構造をたどる
さて、木構造はその定義上ループは含まれていないので、ルートから始めてどんどん先へとたどって行くと、必ず行き止まり=リーフにたどり着きます。そのため、行って戻ってを再帰的に繰り返していくと、すべてのノード・リーフをたどれます。これを深さ優先探索(Depth first search)といいます。
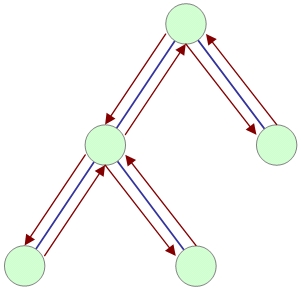
深さ優先探索で木構造をたどる場合には、再帰的に各ノード・リーフのデータを処理するわけですが、どこでデータを処理するかによって取り出し順が3つ存在します。節点の左側は自分より小さい値、右側は大きい値となるように木を構成した場合、以下の「通りがけ順」にたどって行くと、ソートされた結果が返ってきます。
行きがけ順(PREORDER):
- ノードのデータを処理する
- 左側の部分木を行きがけ順で再帰的に処理する
- 右側の部分木を行きがけ順で再帰的に処理する
通りがけ順(INORDER):
- 左側の部分木を通りがけ順で再帰的に処理する
- ノードのデータを処理する
- 右側の部分木を通りがけ順で再帰的に処理する
帰りがけ順(POSTORDER):
- 左側の部分木を帰りがけ順で処理する
- 右側の部分木を帰りがけ順で処理する
- ノードのデータを処理する
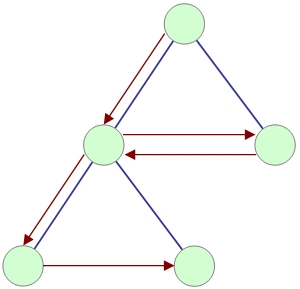
これに対して、上から順に同じ深さのノードをたどって行く方法があります。しらみつぶしにすべてをたどるのであれば、こちらの方が効率がいいですね。幅優先探索(Breadth first search)と呼ばれています。データベースのインデックスとして考えると、Full Index Scanの場合には、こちらを使った方が良いということになるんじゃないかと思います。
 ロシアからやってきたAVL木
ロシアからやってきたAVL木
それではこの木構造をDelphiでクラスとして実装して行きたいと思います。実装するのは平衡二分探索木(self-balancing binaryu search tree)のうち、AVL木とします。AVL木はロシア人の数学者アデルソンヴェルスキ(Georgy Maximovich Adelson-Velsky)とランディス(Yevgeniy Mikhailovich Landis)が考案したもので、以下の2つの特徴を持ちます。
- 2つの子を持つ各節点において、左側部分木と右側部分木の高さが1以内であること
- 1つの子しか持たない各節点において、その子は葉であること
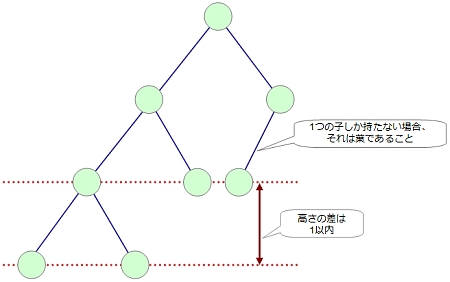
AVL木では、節点を追加するときに、上記のバランスが崩れていないかをチェックしつつ、崩れていればそれを回復する処理を行う必要があります。それだけ手間が掛かるわけですが、バランスを取りながら木の高さを低く保つことで、探索時のコストを抑えることが可能になります。
木がバランスしていない場合、最悪のケースでは上図のように1つずつすべてたどって行かなくてはならないケースも考えられます。この場合は、O記法でいうO(N)のコストが掛かってしまうわけですから、リストと変わらないことになります。
ところが、左右のバランスが取れているのであれば、例えば1000要素あってもlog2(1000)≒10、つまり木の高さは10程度になるわけです。O(log(N))になるので、これはかなり速いことになります。
| 高さ | 各段の要素数 | 合計要素数 |
|---|---|---|
0 |
1 |
1 |
1 |
2 |
3 |
2 |
4 |
7 |
3 |
8 |
15 |
4 |
16 |
31 |
5 |
32 |
63 |
6 |
64 |
127 |
7 |
128 |
255 |
8 |
256 |
511 |
9 |
512 |
1023 |
10 |
1024 |
2047 |
もちろん、探索が速くなるかわりに挿入や削除の際のコストは余計に掛かることになります。そこで増加するコストが莫大なものでないのであれば、探索がひんぱんに行われる場合にはこちらの方が有利になるわけです。
データベースにインデックスを付けるのもまさにこの理由からで、挿入や削除の際には余計なコストが掛かりますが、後々データを参照する際には圧倒的なスピードが実現できます。しかし、挿入や削除が頻繁に行われるときはインデックスを止めますよね。
1/2 |
| Index | |
| AVL木で木構造を学ぼう | |
| Page1 木構造とは何か? 木構造をたどる ロシアからやってきたAVL木 |
|
| Page2 AVL木への節点の追加 Listにそっくりな木構造のクラス アルゴリズムの実装は編み物に似ている |
|
| Appendix AVLTreeのソースコード |
|
| Delphiアルゴリズムトレーニング |
| Coding Edgeお勧め記事 |
| いまさらアルゴリズムを学ぶ意味 コーディングに役立つ! アルゴリズムの基本(1) コンピュータに「3の倍数と3の付く数字」を判断させるにはどうしたらいいか。発想力を鍛えよう |
|
| Zope 3の魅力に迫る Zope 3とは何ぞや?(1) Pythonで書かれたWebアプリケーションフレームワーク「Zope 3」。ほかのソフトウェアとは一体何が違っているのか? |
|
| 貧弱環境プログラミングのススメ 柴田 淳のコーディング天国 高性能なIT機器に囲まれた環境でコンピュータの動作原理に触れることは可能だろうか。貧弱なPC上にビットマップの直線をどうやって引く? |
|
| Haskellプログラミングの楽しみ方 のんびりHaskell(1) 関数型言語に分類されるHaskell。C言語などの手続き型言語とまったく異なるプログラミングの世界に踏み出してみよう |
|
| ちょっと変わったLisp入門 Gaucheでメタプログラミング(1) Lispの一種であるScheme。いくつかある処理系の中でも気軽にスクリプトを書けるGaucheでLispの世界を体験してみよう |
|
- プログラムの実行はどのようにして行われるのか、Linuxカーネルのコードから探る (2017/7/20)
C言語の「Hello World!」プログラムで使われる、「printf()」「main()」関数の中身を、デバッガによる解析と逆アセンブル、ソースコード読解などのさまざまな側面から探る連載。最終回は、Linuxカーネルの中では、プログラムの起動時にはどのような処理が行われているのかを探る - エンジニアならC言語プログラムの終わりに呼び出されるexit()の中身分かってますよね? (2017/7/13)
C言語の「Hello World!」プログラムで使われる、「printf()」「main()」関数の中身を、デバッガによる解析と逆アセンブル、ソースコード読解などのさまざまな側面から探る連載。今回は、プログラムの終わりに呼び出されるexit()の中身を探る - VBAにおけるFileDialog操作の基本&ドライブの空き容量、ファイルのサイズやタイムスタンプの取得方法 (2017/7/10)
指定したドライブの空き容量、ファイルのタイムスタンプや属性を取得する方法、FileDialog/エクスプローラー操作の基本を紹介します - さらば残業! 面倒くさいエクセル業務を楽にする「Excel VBA」とは (2017/7/6)
日頃発生する“面倒くさい業務”。簡単なプログラミングで効率化できる可能性がある。本稿では、業務で使うことが多い「Microsoft Excel」で使えるVBAを紹介する。※ショートカットキー、アクセスキーの解説あり
|
|





