 AVL木への節点の追加
AVL木への節点の追加
さて、AVL木に新しくデータが追加された場合、それがどの節点とも一致しなければ節点を追加することになります。そして、新しく節点が追加されたことで先に挙げたAVL木のバランス条件が崩れた場合には、平衡を取り戻す処理を実施しなくてはなりません。
AVL木では節点の追加位置によって以下の4つのパターンが存在することが分かっています。
- R(右回転)
- L(左回転)
- LR(左−右回転)
- RL(右−左回転)
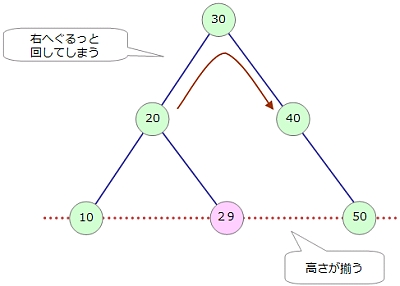
右回転を例に見ていきましょう。まず、初期状態は下図のようになっているものと考えます。先に挙げた「通りがけ順」でたどっていくと、「10、20、30、40、50」とソートされた順でたどれることがわかりますね。
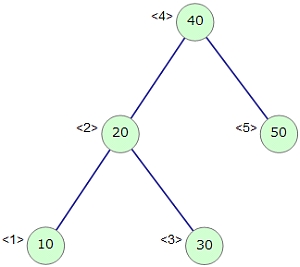
この状態のツリーに「9」の要素を追加してみます。自分より小さい値は左側なので、ROOTからたどっていって、「10」の葉の左側に追加することになります。ところが、この状態になると木の高さのバランスが崩れてしまいます。
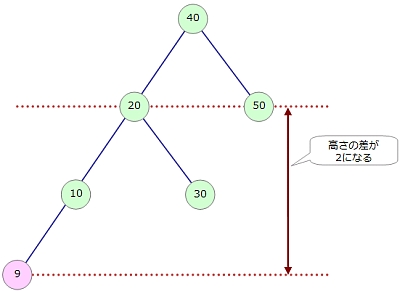
そこで、見た目でぐるっと右側へ20の節点を上に引き上げるようなカタチで回転させると、木の高さの差が1になって、しかも左右のバランスが崩れずに済みます。
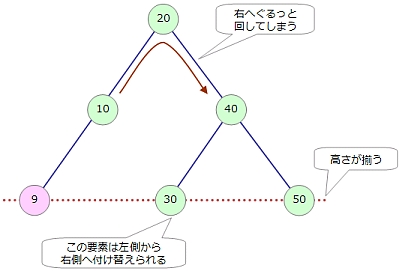
同じように左側の木の右側、つまりLRの位置に節点が追加された場合にはどのようにすべきかを見ていきます。
親と子、左と右を入れ替えながら、ぐるっと左に回すようにしてから……
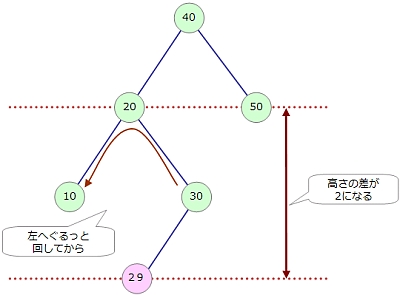
さらに右側へぐるっと回すように処理をすると、バランスが回復されます。
木の右側に節点を追加するときも同じように、左回転、右−左回転を行うと木のバランスが回復しますが、図説については同様なので割愛します。
 Listにそっくりな木構造のクラス
Listにそっくりな木構造のクラス
さて、それではAVL木をクラスとして実装していきましょう。クラスとしての外形的な特徴は以下のとおりです。
TAVLTreeクラスの定義:
- TAVLTreeは複数のデータを保持することができる
- インデックスを指定して、データを挿入することができる
- インデックスを指定して、データを参照することができる
- インデックスを指定して、データを更新することができる
- インデックスを指定して、データを削除することができる
なんだか、Listとそっくりですね。結局、やりたいことは何らかのインデックスを与えてデータをCRUDしたいということなので、外形的には同じものになってしまいます。データの操作に関して、それぞれのアルゴリズムとデータ構造に従って、ある操作が速かったり遅かったりするというのが違いになるわけです。
AVLTreeからの削除については、手順を別途検討しなくてはいけないので、今回はデータを挿入したり参照したりできるところまで実装することにします。また、ツリーの内部構造を表示させたいので、DumpNodesというメソッドを用意しました。先に紹介した、行きがけ順・通りがけ順・帰りがけ順でツリーをたどったときに、各ノードのIDをそれぞれの処理順で文字列で返します。
001: unit avltree;
002:
003: interface
004:
005: uses
006: SysUtils, Classes, RTLConsts;
007:
008: type
009: TBalance = (brLeft, brEqual, brRight);
010: TDumpNodes = (dnPreorder, dnInorder, dnPostorder);
011: TAVLNode = class;
012:
013: TAVLNode = class(TObject)
014: private
015: FItem : Pointer;
016: public
017: ID : Integer;
018: LeftChild, RightChild : TAVLNode;
019: Balance : TBalance;
020: property Item : Pointer read FItem write FItem;
021: constructor Create;
022: destructor Destroy; override;
023: end;
024:
025: TAVLTree = class(TObject)
026: private
027: FCount : integer;
028: FRoot : TAVLNode;
029: protected
030: procedure AddNode(var parent : TAVLNode; newID : Integer; value : Pointer; var grow : Boolean);
031: procedure AdjustLeftGrow(var parent : TAVLNode);
032: procedure AdjustRightGrow(var parent : TAVLNode);
033: function Get(Index: Integer): Pointer;
034: function InternalGet(var parent: TAVLNode; index : integer; var bolFind:Boolean):pointer;
035: procedure InternalDumpNodes(var parent : TAVLNode; var s : string; search_algo:TDumpNodes);
036: public
037: procedure Add(newID : Integer; value : Pointer);
038: function DumpNodes(search_algo:TDumpNodes):String;
039: property Count : Integer read FCount;
040: property Items[Index: Integer]: Pointer read Get; default;
041: destructor Destroy; override;
042: end;
043:
044: implementation
045:
046:
047: { TAVLNode }
048:
049: constructor TAVLNode.Create;
050: begin
051: //
052: end;
053:
054: destructor TAVLNode.Destroy;
055: begin
056: if (LeftChild <> nil) then LeftChild.Free;
057: if (RightChild <> nil) then RightChild.Free;
058:
059: inherited;
060: end;
061:
062: { TAVLTree }
063:
064: //ツリーに値を追加する処理
065: procedure TAVLTree.Add(newID: Integer; value: Pointer);
066: var
067: grow : Boolean;
068: begin
069: //Addメソッドは、まずRootから値を追加する先を探索する
070: grow := False;
071: AddNode(FRoot, newID, value, grow);
072: end;
073:
074: //ノードの追加を再帰的に行う処理
075: procedure TAVLTree.AddNode(
076: var parent: TAVLNode;
077: newID: Integer;
078: value : Pointer;
079: var grow: Boolean
080: );
081: begin
082: //木の最深部まで降りた場合、そこにノードを追加する
083: if (parent = nil) then
084: begin
085: parent := TAVLNode.Create;
086: parent.ID := newID;
087: parent.Balance := brEqual;
088: parent.Item := value;
089: grow := True;
090: Inc(FCount);
091: exit;
092: end;
093:
094: //newIDが現在の節点のIDより小さい時の処理
095: //左側に下っていく
096: if (newID < parent.ID) then
097: begin
098: //左側へ節点を追加する
099: AddNode(parent.LeftChild, newID, value, grow);
100:
101: //木が成長した=高さが変わった場合、grow がTrueで返ってくる
102: //Falseの場合、バランス調整は不要
103: if (grow = False) then exit;
104:
105: if (parent.Balance = brRight) then
106: begin
107: //元々は右側の高さが大きかった場合
108: //左に新しい節点が追加されたので、これでバランスした
109: parent.Balance := brEqual;
110:
111: //上のノードには、深度が変化していないと通知する
112: grow := False;
113: end else if (parent.Balance = brEqual) then
114: begin
115: //元々がバランスしていたので、左側に節点が追加されたため
116: //左側が深い状態になった
117: parent.Balance := brLeft;
118: end else
119: begin
120: //元々左側の高さが大きかったので、
121: //左側に節点が追加されたため、バランス調整が必要となった
122: AdjustLeftGrow(parent);
123: grow := False;
124: end;
125:
126: end else
127: //newIDが現在の節点のIDより大きい場合の処理
128: //右側に下っていく
129: if (newID > parent.ID) then
130: begin
131: //右側に節点を追加する
132: AddNode(parent.RightChild, newID, value, grow);
133:
134: //木が成長した=高さが変わった場合、grow がTrueで返ってくる
135: //Falseの場合、バランス調整は不要
136: if (grow = False) then exit;
137:
138: if (parent.Balance = brLeft) then
139: begin
140: //元々は左側の高さが大きかった場合
141: //右に新しい節点が追加されたので、これでバランスした
142: parent.Balance := brEqual;
143: grow := False;
144: end else
145: if (parent.Balance = brEqual) then
146: begin
147: //元々がバランスしていたので、右側に節点が追加されたため
148: //右側が深い状態になった
149: parent.Balance := brRight;
150: end else
151: begin
152: //元々右側の高さが大きかったので
153: //右側に節点が追加されたため、バランス調整が必要になった
154: AdjustRightGrow(parent);
155: grow := False;
156: end;
157: end else
158: begin
159: //newIDと現在の節点のIDが同じ場合は、ノードの値を書き換える
160: parent.Item := value;
161: grow := False;
162: end;
163: end;
164:
165: //ツリーの左側でバランスが崩れたときの処理
166: procedure TAVLTree.AdjustLeftGrow(var parent: TAVLNode);
167: var
168: OrgLeftChild, OrgGrandChild : TAVLNode;
169: begin
170: OrgLeftChild := parent.LeftChild;
171: if (OrgLeftChild.Balance = brLeft) then
172: begin
173: //左側の左側でバランスが崩れたので、右回転する
174: parent.LeftChild := OrgLeftChild.RightChild;
175: OrgLeftChild.RightChild := parent;
176: parent.Balance := brEqual;
177: parent := OrgLeftChild;
178: end else
179: begin
180: //左側の右側でバランスが崩れたので、左−右回転する
181: OrgGrandchild := OrgLeftchild.RightChild;
182: OrgLeftchild.RightChild := OrgGrandChild.LeftChild;
183: OrgGrandchild.LeftChild := OrgLeftchild;
184: parent.LeftChild := OrgGrandChild.RightChild;
185: OrgGrandChild.RightChild := parent;
186: if (OrgGrandChild.Balance = brLeft) then
187: parent.Balance := brRight
188: else
189: parent.Balance := brEqual;
190: if (OrgGrandchild.Balance = brRight) then
191: OrgLeftchild.Balance := brLeft
192: else
193: OrgLeftchild.Balance := brEqual;
194: parent := OrgGrandChild;
195: end;
196: parent.Balance := brEqual;
197: end;
198:
199: //ツリーの右側でバランスが崩れたときの処理
200: procedure TAVLTree.AdjustRightGrow(var parent: TAVLNode);
201: var
202: OrgRightChild, OrgGrandChild : TAVLNode;
203: begin
204: OrgRightChild := parent.RightChild;
205: if (OrgRightChild.Balance = brRight) then
206: begin
207: //右側の右側でバランスが崩れたので、左回転する
208: parent.RightChild := OrgRightChild.LeftChild;
209: OrgRightChild.LeftChild := parent;
210: parent.Balance := brEqual;
211: parent := OrgRightChild;
212: end else
213: begin
214: //右側の左側でバランスが崩れたので、右−左回転する
215: OrgGrandchild := OrgRightchild.LeftChild;
216: OrgRightchild.LeftChild := OrgGrandChild.RightChild;
217: OrgGrandChild.RightChild := OrgRightChild;
218: parent.RightChild := OrgGrandChild.LeftChild;
219: OrgGrandChild.LeftChild := parent;
220: if (OrgGrandChild.Balance = brRight) then
221: parent.Balance := brLeft
222: else
223: parent.Balance := brEqual;
224: if (OrgGrandchild.Balance = brLeft) then
225: OrgRightChild.Balance := brRight
226: else
227: OrgRightChild.Balance := brEqual;
228: parent := OrgGrandChild;
229: end;
230: parent.Balance := brEqual;
231: end;
232:
233: destructor TAVLTree.Destroy;
234: begin
235: if (FRoot <> nil) then FRoot.Free;
236:
237: inherited;
238: end;
239:
240: //ツリーの内部からIDを引き出して、文字列で返す
241: function TAVLTree.DumpNodes(search_algo:TDumpNodes): String;
242: begin
243: InternalDumpNodes(FRoot, result, search_algo);
244: end;
245:
246: //ツリーのインデックス参照による値の取得
247: function TAVLTree.Get(Index: Integer): Pointer;
248: var
249: bolFind:Boolean;
250: begin
251: Result := InternalGet(FRoot, Index, bolFind);
252: if (bolFind = False) then raise EListError.Createfmt(LoadResString(@SListIndexError), [Index]);
253: end;
254:
255: //ツリーの内部状態をダンプする処理
256: procedure TAVLTree.InternalDumpNodes(var parent: TAVLNode; var s: string; search_algo:TDumpNodes);
257: procedure make_result;
258: begin
259: if (s <> '') then s := s + ', ';
260: s := s + 'ID=' + IntToStr(parent.ID);
261: end;
262: begin
263: //行きがけ順はここで処理
264: if (search_algo = dnPreorder) then make_result;
265:
266: if (parent.LeftChild <> nil) then InternalDumpNodes(parent.LeftChild, s, search_algo);
267:
268: //通りがかけ順はここで処理
269: if (search_algo = dnInorder) then make_result;
270:
271: if (parent.RightChild <> nil) then InternalDumpNodes(parent.RightChild, s, search_algo);
272:
273: //帰りがけ順はここで処理
274: if (search_algo = dnPostorder) then make_result;
275: end;
276:
277: //ツリーからのデータの取得を再帰的に行う処理
278: function TAVLTree.InternalGet(var parent: TAVLNode; index : integer; var bolFind:Boolean): pointer;
279: var
280: tmp:Pointer;
281: begin
282: if (parent.ID = Index) then
283: begin
284: result := parent.item;
285: bolFind := True;
286: exit;
287: end;
288: if (parent.LeftChild <> nil) then
289: begin
290: tmp := InternalGet(parent.LeftChild, index, bolFind);
291: if (bolFind = True) then
292: begin
293: result := tmp;
294: exit;
295: end;
296: end;
297: if (parent.RightChild <> nil) then
298: begin
299: tmp := InternalGet(parent.RightChild, index, bolFind);
300: if (bolFind = True) then
310: begin
302: result := tmp;
303: exit;
304: end;
305: end;
306: end;
307:
308: end.テストプログラムも作成してみました。AVLTree_Text.exeを実行してみて下さい。ツリーへの挿入は、Add(newID : Integer; value : Pointer)というメソッドで行いますが、newIDがすでに格納されている場合は、Valueを上書きするようにしました。
要素の参照はプロパティItems[Index: Integer]をとおして行いますが、default指定を付けてあるので、ツリーのインスタンスに対して[Index: Integer]とすればアクセスできます。なお、AVLTree_Text.exeのソースコードを公開します(avltreetest.zip)。
 アルゴリズムの実装は編み物に似ている
アルゴリズムの実装は編み物に似ている
リストやキューもそうですが、データの追加や削除を行う際の処理というのは、ある種、編み物やあやとりに似ているなと思います。こちらとあちらを切り離して、こちらへ付け替えて、という感じですね。
アルゴリズムを実装するというのは編み物で、実は僕らは羊毛で機織りをしているのと変わらないのかもしれません。10歳の娘が編み物にチャレンジしていましたが、見てると頭がこんがらがりそうなくらい難しいですからね。それにしれも、あれは誰にあげるんだろう……。
さて、次回は今回の続きでAVLTreeからの節点の削除にチャレンジしてみます。ご期待下さい。
2/2 |
| Index | |
| AVL木で木構造を学ぼう | |
| Page1 木構造とは何か? 木構造をたどる ロシアからやってきたAVL木 |
|
| Page2 AVL木への節点の追加 Listにそっくりな木構造のクラス アルゴリズムの実装は編み物に似ている |
|
| Appendix AVLTreeのソースコード |
|
| Delphiアルゴリズムトレーニング |
| Coding Edgeお勧め記事 |
| いまさらアルゴリズムを学ぶ意味 コーディングに役立つ! アルゴリズムの基本(1) コンピュータに「3の倍数と3の付く数字」を判断させるにはどうしたらいいか。発想力を鍛えよう |
|
| Zope 3の魅力に迫る Zope 3とは何ぞや?(1) Pythonで書かれたWebアプリケーションフレームワーク「Zope 3」。ほかのソフトウェアとは一体何が違っているのか? |
|
| 貧弱環境プログラミングのススメ 柴田 淳のコーディング天国 高性能なIT機器に囲まれた環境でコンピュータの動作原理に触れることは可能だろうか。貧弱なPC上にビットマップの直線をどうやって引く? |
|
| Haskellプログラミングの楽しみ方 のんびりHaskell(1) 関数型言語に分類されるHaskell。C言語などの手続き型言語とまったく異なるプログラミングの世界に踏み出してみよう |
|
| ちょっと変わったLisp入門 Gaucheでメタプログラミング(1) Lispの一種であるScheme。いくつかある処理系の中でも気軽にスクリプトを書けるGaucheでLispの世界を体験してみよう |
|
- プログラムの実行はどのようにして行われるのか、Linuxカーネルのコードから探る (2017/7/20)
C言語の「Hello World!」プログラムで使われる、「printf()」「main()」関数の中身を、デバッガによる解析と逆アセンブル、ソースコード読解などのさまざまな側面から探る連載。最終回は、Linuxカーネルの中では、プログラムの起動時にはどのような処理が行われているのかを探る - エンジニアならC言語プログラムの終わりに呼び出されるexit()の中身分かってますよね? (2017/7/13)
C言語の「Hello World!」プログラムで使われる、「printf()」「main()」関数の中身を、デバッガによる解析と逆アセンブル、ソースコード読解などのさまざまな側面から探る連載。今回は、プログラムの終わりに呼び出されるexit()の中身を探る - VBAにおけるFileDialog操作の基本&ドライブの空き容量、ファイルのサイズやタイムスタンプの取得方法 (2017/7/10)
指定したドライブの空き容量、ファイルのタイムスタンプや属性を取得する方法、FileDialog/エクスプローラー操作の基本を紹介します - さらば残業! 面倒くさいエクセル業務を楽にする「Excel VBA」とは (2017/7/6)
日頃発生する“面倒くさい業務”。簡単なプログラミングで効率化できる可能性がある。本稿では、業務で使うことが多い「Microsoft Excel」で使えるVBAを紹介する。※ショートカットキー、アクセスキーの解説あり
|
|





