第179回 ムーアの法則が50年、どこまで続く「18カ月で2倍」の法則:頭脳放談
ムーアの法則が、2015年で50年を迎えたという。半導体の集積度が時間発展とともに「18カ月で2倍」になるというもの。いまだに続くこの法則だが、そろそろ限界なのか、それともさらに続くのか。
今さらであるが、インターネットのご時世になってからというもの、情報のあふれ方は加速している。まさに指数関数的といえる。氾濫する情報が真実ばかりであればまだしもであるが、虚報、ガセネタの類もあふれかえっているのはご承知の通り。
人から人へと情報が流れていくときに前提条件が脱落し、結果だけが独り歩きする、また知ってか知らでか誤りが混入するということは避けらないようだ。また真贋にかかわらず面白い情報は流布する。本稿も嘘つきにならないように気を配らないとならない。しかし、嘘にはならなくても、広まり過ぎてご本人が言った覚えのないところまで尾ひれが付いて拡大解釈される言葉や考えというものはあるようだ。
いわゆる「人口(じんこう)に膾炙(かいしゃ)する(広く知れ渡り、もてはやされること)」という状態かもしれない。これから取り上げさせていただく「ムーアの法則」というものも、IT系の業界に広く知れ渡っている。そして筆者も、世話になっているまさにその一人なのだが、あちらこちらで「ムーアの法則によれば」などとたびたび引用されている。この「法則」、発表されてから2015年の今年で50年なのだそうだ(1965年4月19日号の「Electronics」誌に発表された「Cramming more components onto integrated circuits」というタイトルの論文で発表されている。なお、この当時ムーア博士はIntelの設立前で、Fairchild Semiconductorに在籍していた)。
ムーア博士は「ご本人」などと気安く呼ぶのははばかられる半導体業界の巨人であるが、あえてご本人がこの「法則」を提案したころを想像してみる。半導体業界はまだ海のものとも山のものとも分からないごくごくささやかな「産業の芽」くらいなところである。それどころか実は、真の売り先もまだはっきりはしていない。
若い人に断っておくと、この時代にはパソコンもスマホも存在していない。「いろいろ使える」「これは化ける」という予想はされていたようだが、今ほどにコンピューターもエレクトロニクスも発展していないから、誰も今のような状態を予想していたわけではない。そこに新進気鋭の研究者にして自分の研究をそのまま産業化まで持って行こうとする起業家として、博士がいるわけだ。多分、その念頭にあった適用範囲は、専門の半導体業界の中に限定された範囲であったに違いない。
そこで、立ち上がりつつある業界の将来にわたる急速な発展を見抜き、半導体の集積度が時間発展とともに「18カ月で2倍」といった指数関数的に上昇するという意見を唱えられたわけだ。実際には18カ月で2倍という定数を最初から提唱していたという話は、どうも尾ひれの類のようで怪しいが、産業の立ち上がりのごくごく初期の段階で、指数関数的という「経験則」を見抜いたことが偉大だと捉えられているようだ。
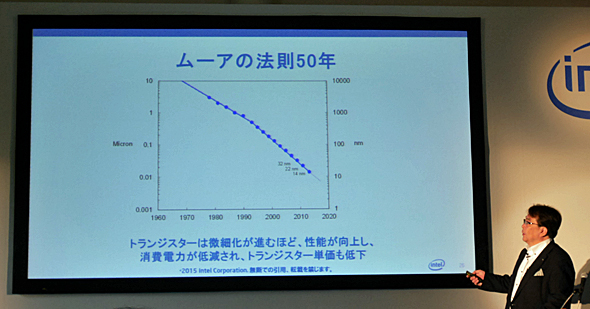
トランジスターの微細化の流れ
トランジスターの微細化はムーア氏が予測したように進んでおり、その効果により性能の向上や消費電力の低減を実現し、単価も急速に低下しているという。2015年4月21日開催されたインテルの「ムーアの法則50周年記者説明会」でのインテルの取締役兼副社長執行役員の阿部剛士氏のプレゼンテーションより。
しかし、見抜いたことが偉大だったんだろうか? 最近はいざ知らず、ふた昔前くらいに半導体設計・製造に携わっていた人であれば覚えていると思うのだが、ある旧世代の半導体製造プロセスから次の新世代のプロセスに移行するときには、半導体屋はすべからく、「コンマ8掛け」つまり長さ方向で8割か、「コンマ64掛け」つまり8割X8割で6割4分、といっためでたい末広がりのマジックナンバーで仕事をしていた。コンマ64掛けの場合、長さ方向で6割4分、面積では単純2乗して約4割となるが、半導体チップには簡単には縮小できない周辺部があって足を引っ張るので大体面積は2分の1となる。
つまり、半導体屋はすべからく決まった定数掛けの系列上で働いていたわけで、ある世代から次の世代へと一定のタイムスパンで開発が成功していけば、何のことはない、時間に対して指数関数的な集積度の向上が自然と達成されたわけである。そして、そのような系列を可能にしていたものこそ、「比例縮小則」と呼ばれる半導体の物理的特性から求められた設計原則であった。
ムーア大先生とその世代の方々が偉大であったのは、それ以降の半導体屋が比例縮小則に基づいて仕事をできるような業界の基盤を、技術的にも資本的にも確立したことではないか、と思っている、筆者自身の勝手な意見としては、だが。
縮小という軸のステップはある意味物理的な制約に基づいていたが、もう一方の軸である開発速度の多くは、人為的なパラメーターによる。ムーアの法則は「自然法則ではない」といわれるゆえんである。いわゆる「ヒト」「モノ」「カネ」の世界だ。半導体業界が急速に発展していたころ、「ヒト」「モノ」「カネ」も急速に業界になだれ込んだ。そのころ、どこの半導体会社も必ず自社のロードマップなるものを示して、自社の発展の方向とタイムスケジュールを発表するのがお約束となっていた。そのとき基準となっていたものこそ、ムーアの法則の「18カ月で2倍」というマジックナンバーであった。
同業他社はムーアの法則通りの速度で発展する「はず」なのである。そこで自社だけがムーアの法則に後れを取ったとしたら脱落してしまう。先を取ろうとすればムーアの法則の「定数」以上を狙わなければならない。当時の半導体屋の広告や発表をみれば「ムーアの法則を超える」などという言葉があふれていたものだ。一歩でも先行したい基準のベンチマークであり、全ての業界ロードマップの根底に、この法則が置かれていたといっても過言ではなかったと思う。
それは簡単な目標ではなかったが、みんながそれを目指して競争した。あるものは一時それを超えたかもしれないが、何世代も先行したものはいない。誰かは脱落したが、誰かが成功した。そして結果、法則通りの発展が長く守られることとなったように思われる。何十年か法則は常に正しく、信じられることとなったのだ。しかし、法則の前途に暗雲を見ていた人は多い。
前にも指摘したことだが、指数関数は無限に向かって急激に大きくなる。有限なこの世界でXX%成長などという指数関数的な挙動が長いこと続けられるわけはないことは、数学的に明らかだ。こと半導体の場合、集積度の上昇は最少寸法の縮小を意味したから、その限界はそう遠くない将来に来るものと早くから予想されていたのだ。
原子の大きさを超えて小さくできるはずもないから止まると。いや2次元配置を3次元化すれば次元を増やした分だけまだトレンドは続けられると。だが、まずその前に、あの比例縮小則が崩れた。比例縮小則は大きさの縮小とともに電圧をも「縮小」することが要求事項に含まれているのだが、それが難しくなったからだ。その後は微細化に伴う難題が次々と到来する。
一昔前からは、世代ごとに必死の努力を重ねて何とか微細化を続け、集積度を上げてきたように見える。その上、半導体産業自体が成熟した。勝手に巨大な産業となったが、ヒトもカネも急激に増加したころのようにはいかない。オリジナルの想定範囲であったはずの半導体の集積度という点では、すでにムーアの法則はその限界に突き当たっていて、実際18カ月で2倍の定数は落ちているのではないかと感じられる。
ところが、ムーアの法則は不滅である。もともとは半導体の集積度についての法則だったのが、どんどん適用範囲を拡大したように思える。その拡大の最初は、マイクロプロセッサーの性能、速度といったものへの適用ではなかったか。まぁ、マイクロプロセッサーの性能自体、半導体の集積度と深い関係があるのだから、無謀に適用範囲を広げたという感じもない。それにムーア博士らが設立したIntelがそれを言うのだから、なおさら自然であった。この分野へのムーアの法則の適用もまずは認知され、そこからコンピューターや情報機器の進歩など数々のものに演繹(えんえき)されていくようになったようだ。
そんな中、マイクロプロセッサーのクロック速度の上昇については熱的な障壁からすぐに頭打ちとせざるを得なくなった。「法則」を適用できたのは、ある短い期間についてであり、いつの間にかこの件は聞かなくなった。何せ指数関数である。年率何%といった上昇を示すものであれば、何にでも当てはまる汎用性がある。それなりに背景のある現象に当てはめるのであれば理解できるのだが、たまたまそう見えるところに無理やりに当てはめるのはムーアの法則の名を借りた正当化でしかない。
とはいえ、使い方がひとたび広がったものは止めようがない。おかげでアチラコチラにムーアの法則がはびこり、最近では半導体業界の枠組みさえ超えてしまったようだ。はびこる拡張版ムーアの法則にも、その真贋なのか、適用可能期間なのかを吟味すべきときであろう。
筆者紹介
Massa POP Izumida
日本では数少ないx86プロセッサーのアーキテクト。某米国半導体メーカーで8bitと16bitの、日本のベンチャー企業でx86互換プロセッサーの設計に従事する。その後、出版社の半導体事業部などを経て、現在は某半導体メーカーでヘテロジニアス マルチコアプロセッサーを中心とした開発を行っている。
「頭脳放談」
Copyright© Digital Advantage Corp. All Rights Reserved.