3000万以上のユーザーに未経験サービスを促すギフト券配信の割当問題、数理最適化と機械学習でどう解決したか:リクルート事例で分かる数理最適化入門(3)
リクルートにおける数理最適化の応用事例を通じて、数理最適化とは何か、どのようにビジネスに応用できるのかを紹介する連載。今回は、3000万以上のユーザーに未経験サービスを促すギフト券配信の割当問題、CMの出稿割当問題をどう解決したかを解説する。
本連載「リクルート事例で分かる数理最適化入門」では、リクルートでの数理最適化の応用事例の紹介を通して、数理最適化がどのようにビジネス応用できるのかを紹介します。連載第3回の今回と次回の第4回では、前回に引き続き、リクルート各サービスにおける数理最適化の応用事例を紹介します。
今回は2つの応用事例を紹介しますが、アルゴリズム観点では、それぞれ次のような難しさがありました。
- ホットペッパービューティーでのギフト券配信対象者の決定:問題の構造は平易だが、大規模なので難しい
- CMの出稿割り当ての決定:問題の構造が複雑で、定式化が難しい
上記の課題は、本事例に限らず、数理最適化をビジネス応用する際に頻繁に現れます。今回紹介するアプローチが、読者の皆さんが数理最適化を用いる際の一助になれば幸いです。
ホットペッパービューティーでのギフト券配信対象者の決定
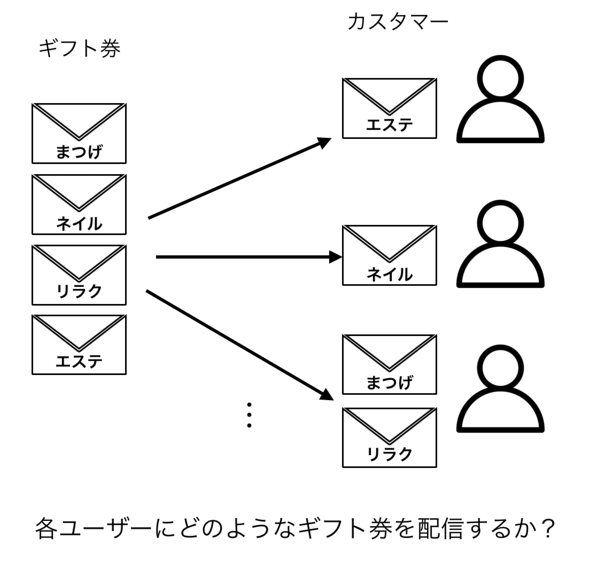
「ホットペッパービューティー」は美容関連サービスのユーザーとクライアントを結び付けるプラットフォームです。大きく、美容院や理容室を予約できる「ヘア領域」と、まつげ/ネイルサロンの予約ができる「リラク&ビューティー領域」の2つで構成されています。リラク&ビューティー領域はまつげやネイルに加えて、リラクセーション、エステの4ジャンルから構成されています。
ホットペッパービューティー会員については、ヘア領域のサービス利用経験者は多いものの、リラク&ビューティー領域の各ジャンルの利用経験がないユーザーが多く存在している状況でした。そこで未経験ジャンルの利用を促すために特定ジャンルで利用ができるギフト券が開発され、各ジャンルにおける新規利用ユーザー創出を目指すこととなりました。
従来の配信ロジックは、属性情報を基にユーザーを分類し、属性単位でどのようなギフト券を配信するかを決定するものでした。しかし、属性情報だけでは個人ごとの予約周期や、最終予約からの経過日数などの行動情報を考慮できず、「ユーザーにとって適切な配信ができている」とは言い難い状況でした。そこでユーザーごとにギフト券の利用を予測するという打ち手が考えられますが、素朴に予測利用数を最大化するような配信では、決められた予算を超えてしまったり、大幅に余らせてしまったりなどから調整が難しいという課題がありました。
ビジネス課題
利用経験のないジャンルがある全ユーザーに対してギフト券を配信したい一方で、予算を逸脱しない範囲でのギフト券配信が事業制約として課されます。よって、ギフト券配信対象者を決定する問題は、予算制約の下でユーザーの新ジャンル利用機会を最大化するようなギフト券の「割当問題」として捉えることができます。
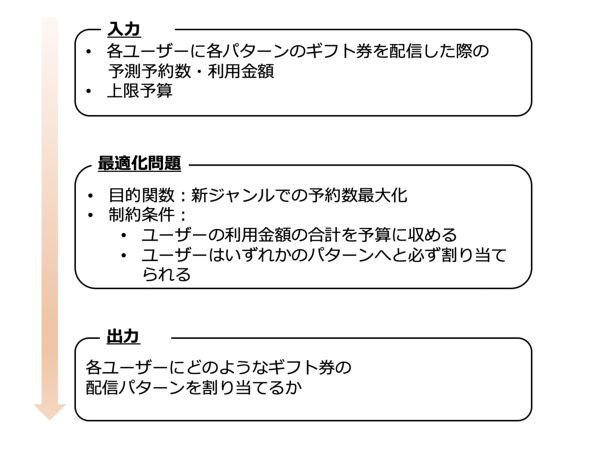
上記の問題を取り扱う上で下記の情報が必要となります。
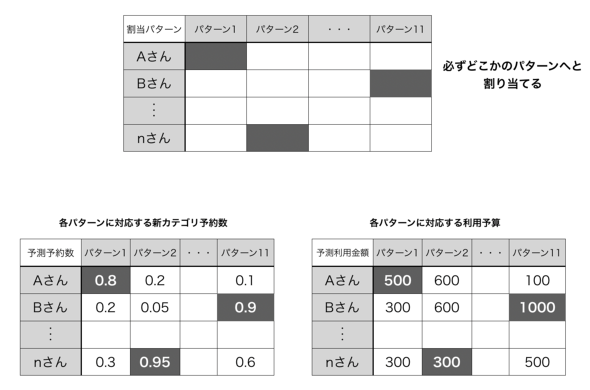
- 各ユーザーに各パターンのギフト券を渡した際の新カテゴリー予約数および利用金額
例:Aさんに
┣ まつげのギフト券を渡した場合(パターン1)の予約数、利用金額
┣ ネイルのギフト券を渡した場合(パターン2)の予約数、利用金額
┗ まつげ/ネイルのギフト券を渡した場合(パターン3)の予約数、利用金額
:
:
Bさんに…… - 今回のキャンペーンにおける予算制約(ユーザーの利用金額の合計をキャンペーン予算に収める必要がある)
※ここでは簡単に表現するために、「1ユーザーに配信できるギフト券は最大2枚」とします。また、各ユーザーはちょうど1つのパターンに割り当てられるとします(今回のケースでは11のパターンが存在することになります)。
これらの情報をインプットとして最終的に得たいものは「各ユーザーに対してどのようなパターンでギフト券を配信すると、新ジャンルでの予約数を最大化できるのか」という割り当てパターンです。
数理最適化によるアプローチ
・入力データの準備
先ほど、割り当てパターンを決定するために「各ユーザーに 各パターンのギフト券を渡した際の新カテゴリー予約数および利用金額」の値が必要になると述べました。これらは、あくまで「それぞれのパターンに対応するギフト券の組み合わせを、もし渡したならば」という仮定の話であり、実績値があるわけではありません。そのため、本案件では機械学習モデルによる予測値を用いています。具体的には、各ユーザーに各パターンのギフト券を配信したときに見込まれる、新ジャンルでの予約数および利用金額を予測しています
これらのモデルの学習データとしては、過去施策におけるギフト券の配信情報とそこにひも付くユーザーの新ジャンルにおける予約データを用いています。
・アルゴリズム
この配信パターンの決定は、「マス目の色塗り(0/1の割り当て)」のような割当問題として捉えることができます。各マス目にはそれぞれ、制約条件となる予算、今回最大化したい新ジャンルでの予約数がそれぞれひも付いています。
このような割当問題のバリエーションはNP困難ではあるものの、数理最適化の汎用(はんよう)ソルバーを用いて解を得やすいタイプです。ただ、今回は3000万以上という付与対象数に起因して、問題が非常に大規模となっており、汎用ソルバーでの求解が困難となるケースに該当します。本案件では、専用アルゴリズムを開発して近似解を得ることで、この問題に対処しています。
導入による効果
従来のセグメント単位でのギフト券配信ロジックに比べて、同じキャンペーン予算当たりの新ジャンル利用者数を、全てのジャンルにおいて増やすことができました。これによって、ユーザーにとって今まで利用経験がなかったカテゴリーやサロンとの出会いを促すことができ、クライアントにとっても新たな顧客の獲得を促すことができました。
結果として、ユーザーとクライアント双方にとってのメリットを生み出すことができたと考えられます。
CMの出稿割り当ての決定
リクルートでは、広告媒体の一つとしてTVのCMを利用しています。「限られたCM枠のどの場所にどのCM素材(CMの種類のこと)を流すか」は、広告効果に大きな影響を与える一方でその意思決定は非常に難しい問題です。
アンケート調査の結果から、複数種類のCMを視聴すると広告効果が高まることが確認できていましたが、それを実現する手段がなく、具体的な割り当てはうまく決められない状態でした。本取り組みでは、この割り当てを、数理最適化を用いて決定することで、広告効果の最大化を目指しました。
ビジネス課題の理解
ここでは、詳細な問題設定を説明します。まず「出力として何を得るか」について述べた後、具体的な要件について説明します。
CMは、大まかに言って次の流れで出稿されます。
- CMの出稿量を決め、広告代理店に発注する
- TV局からCMを放映する枠(放送局×放送開始時刻)を指定される
- 与えられた出稿枠に対して、放映するCM素材を決定する
今回、数理最適化を導入するのは、上記の流れの3番目です。すなわち、最適化の出力は、「TV局から指定された出稿枠の、どの枠にどのCM素材を割り当てるか」です。
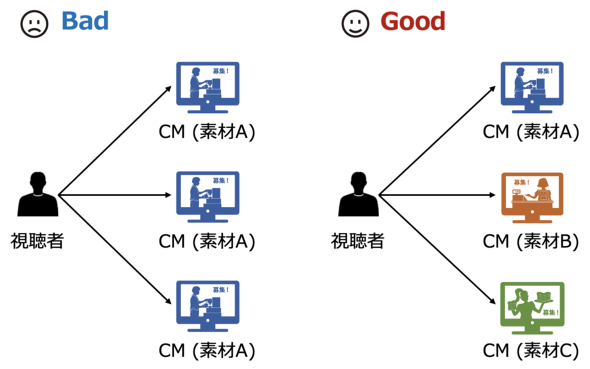
次に、ビジネス的な要件について説明します。冒頭で述べたアンケートの結果から、視聴者に複数のCM素材を視聴してもらうことがリクルートとして望ましい状態です。そこで数理最適化では、「キャンペーン期間中に全てのCM素材を視聴した視聴者数の最大化」を目的とします。
さらに、次のような制約を守る必要があります。
- TV局から指定された出稿枠にしか出稿できない
- 各CM素材で最低限担保したい延べ視聴率(GRP)を保証する
1番目の制約は、今回の問題設定上、必須の制約です。2番目の制約は、CM素材ごとに極端に偏った出稿になることを防ぐための実務的な制約です。下図を使って補足します。
「延べ視聴率」とは、CMを出稿した場所の平均視聴率×CM本数で計算される指標(CM枠ごとの視聴率の総和)で、CMの露出量を意味します。平易に言い換えると、「それぞれのCM素材を一定量は露出しましょう」という制約です。
なお、数理最適化の目的関数や制約条件に視聴者の視聴行動を使っていますが、これは現在時点で観測不可能な未来の情報なので、機械学習モデルなどを用いて予測し、入力データとする必要があります。
ここまでに説明した問題設定をまとめると、下図のようになります。
数理最適化によるアプローチ
ここまでに説明した問題設定を見て、前章のギフト券の割り当てと近い問題ではないかと思われた方もいるかもしれません。構造としては近い問題ですが、今回の問題には特有の難しさがあります。それは、最適化問題の目的関数の部分です。例えば、「売り上げの最大化」「コストの最小化」と違い、今回は、「全てのCM素材を視聴した視聴者」という条件付きの関数になっており、複雑な構造をしています。
このような典型問題から派生した発展的な問題は、どのように定式化していけばいいのでしょうか?
これに対する一つの答えは、典型的な定式化技法を知ることです。例えば、藤江哲也先生の紹介記事※では、さまざまな定式化技法が紹介されています。典型問題をベースとして、上記のような定式化技法を用いて、実務の問題に合わせてカスタマイズするアプローチは、応用する上で非常に重要です。
※藤江哲也, 「整数計画法による定式化入門」『オペレーションズ・リサーチ』, 57, 2012, 190 - 197.
今回の問題では、「全てのCM素材を視聴するか否か」という補助的な変数を用いることによって、問題をうまく定式化できました。定式化の詳細が気になる方は、ぜひこちらの人工知能学会のアブストラクトをご参照ください。
最適化問題に定式化することができたので、汎用ソルバーを用いて解を求め、CM出稿に適用しました。ソルバーについては本連載の第2回でも触れられているので、こちらも併せてご参照ください。
導入による効果
従来の決め方と比較して、最適化後の割り当てでは、目的関数の「キャンペーン期間中に全てのCM素材を視聴した視聴者数」を飛躍的に向上させることができました。さらに、事後のアンケート調査によって、広告効果の向上も確認できました。今後、社内のさまざまなCMに対して本手法を適用することが期待されます。
おわりに
以上、前回の連載から引き続き、リクルートでの数理最適化案件の実例を2つ紹介しました。本稿を読むことで、「数理最適化案件ってこういう感じなのか」といったイメージを深めていただけるとうれしいです。
筆者紹介
中村圭太
株式会社リクルート プロダクト統括本部 プロダクト開発統括室 データ推進室
2019年にリクルートに新卒入社。入社後はマーケティング関連施策をはじめとしたデータ活用案件を担当。
濱田賢吾
株式会社リクルート プロダクト統括本部 プロダクト開発統括室 データ推進室
2020年にリクルートに新卒入社。データサイエンティストとして、主に数理最適化施策の推進を担当。
棚橋 耕太郎
株式会社リクルート プロダクト統括本部 プロダクト開発統括室 データ推進室
リクルートに入社後、広告配信システムの開発に従事。その後アドバンスドテクノロジーラボに兼務し、量子アニーリングの研究なども行っている。
Copyright © ITmedia, Inc. All Rights Reserved.
関連記事
 無償で利用できる「数理、データサイエンス、AI」の教材を公開 東京大学
無償で利用できる「数理、データサイエンス、AI」の教材を公開 東京大学
東京大学の数理・情報教育研究センターは「数理・データサイエンス・AIモデルカリキュラム」に準拠した教材の無償公開を開始した。クリエイティブ・コモンズ・ライセンス(CC BY-NC-SA)で利用できる。 NVIDIAのGPU4基で「1秒間に1兆の解を探索」 広島大学の研究グループが高速探索手法を開発
NVIDIAのGPU4基で「1秒間に1兆の解を探索」 広島大学の研究グループが高速探索手法を開発
広島大学大学院の教授である中野浩嗣氏らの研究チームは、組み合わせ最適化問題の解を高速に探索する新しい計算方式「アダプティブ・バルク・サーチ」を開発した。著名な組み合わせ最適化問題である「最大カット問題」「巡回セールスマン問題」「ランダム問題」について、いずれも1秒以内で最適解が得られたという。 東芝が組み合わせ最適化問題の新アルゴリズムを開発、世界最速をうたう
東芝が組み合わせ最適化問題の新アルゴリズムを開発、世界最速をうたう
東芝は、FPGAやGPUなどを用いた従来型コンピュータだけで、量子コンピュータよりも10倍速く「組み合わせ最適化問題」の解を得られるアルゴリズムを開発した。従来型コンピュータを使って、低コストで大規模な問題にも対応できる。