時系列分析II―ARMAモデル（自己回帰移動平均モデル）の評価と将来予測：ITエンジニアのためのデータサイエンティスト養成講座（10）（3/4 ページ）

過去の時系列データを基に、将来予測につながるモデルを検討、実際に将来予測を行って検証してみましょう。

[中林紀彦，日本アイ・ビー・エム]

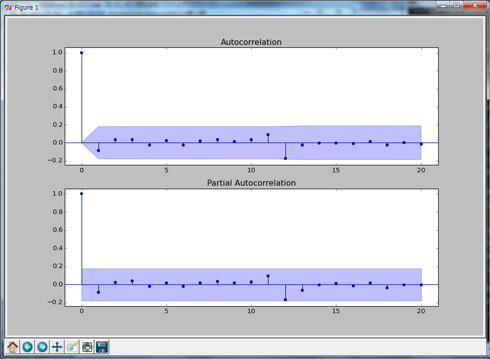
　次に残差についての自己相関（Autocorrelation）プロットと偏自己相関（Partial Autocorrelation）プロットをし、残差に時系列の相関性がないことを確認します（In [48]〜In [55]）。

In [46]: # 前のグラフを閉じる
In [47]: plt.close()
In [48]: # 残差の自己相関（Autocorrelation）プロット
In [49]: fig = plt.figure(figsize=(12,8))
In [50]: ax1 = fig.add_subplot(211)
In [51]: fig = sm.graphics.tsa.plot_acf(resid.values.squeeze(), lags=20, ax=ax1)
In [52]: # 残差の偏自己相関（Partial Autocorrelation）プロット
In [53]: ax2 = fig.add_subplot(212)
In [54]: fig = sm.graphics.tsa.plot_pacf(resid, lags=20, ax=ax2)
In [55]: fig.show()

　図4を見ると、自己相関（Autocorrelation）プロットと偏自己相関（Partial Autocorrelation）プロット双方の値が全て95％の信頼区間にあります。このことから、残差に時系列の相関性はないといえます。よって、このモデルは良好なモデルだと判断できます。

図4　ARMA(13)モデルの残差の自己相関、偏自己相関

　さらに残差は正規分布に従うという特徴がありますので、正規部分布のテストを行うと（In [59]）、p値は2.3193538282769351e-15（Out [59]）と、十分小さい値であり、正しく正規分布に従っていることが確認できます。

In [56]: # 前のグラフを閉じる
In [57]: plt.close()
In [58]: # 残差の正規分布をテスト
In [59]: stats.normaltest(resid)
Out[59]: (67.394975540642861, 2.3193538282769351e-15)

　モデル検証の「ダメ押し」に、Ljung-Box検定もやっておきましょう。この検定の詳細はWikipediaの解説にゆだねますが、モデルが十分に偏りがないことを確認する検定の1種です。Pythonプログラムでは次のようにシンプルに実施できます。

　ラグ値13までのラグに対してLjung-Box検定を行い（In [61]）自己相関（AC）、Q値、p値を表形式で表示します（In [62]〜In [64]）。p値に着目し、十分に大きいことから、残差は無作為であるということができます。

In [60]: # Ljung-Box検定
In [61]: r,q,p = sm.tsa.acf(resid.values.squeeze(), nlags=13, qstat=True)
In [62]: data = np.c_[range(1,14), r[1:], q, p]
In [63]: table = pd.DataFrame(data, columns=['lag', "AC", "Q", "Prob(>Q)"])
In [64]: print table.set_index('lag')
           AC         Q  Prob(>Q)
lag
1   -0.084692  0.882429  0.347537
2    0.032644  1.014639  0.602107
3    0.036035  1.177118  0.758497
4   -0.024990  1.255933  0.868806
5    0.023351  1.325348  0.932302
6   -0.024581  1.402945  0.965679
7    0.018856  1.449008  0.984023
8    0.033126  1.592446  0.991064
9    0.011344  1.609418  0.996251
10   0.033756  1.761073  0.997865
11   0.092489  2.910017  0.991862
12  -0.175171  7.069513  0.852986
13  -0.024540  7.151912  0.894154

　このようにいくつかの観点からARMA(13,0)モデルの妥当性を評価し、統計的に妥当なモデルであるということが証明できました。

コラム：Python環境を最新に

　本連載では何度も紹介していますが、Python本体やいくつかのモジュールがアップデートされています。特にIPythonはメジャーバージョンアップがあり、パフォーマンスがかなり改善されていますし、他のモジュールでもパフォーマンスの改善があります。APIの変更があるものありますので、アップデートの際には注意が必要ですが、影響がなければアップデートをお勧めします。

Python本体　バージョン2.7.8がリリース

ダウンロードURL ： http://python.org/download/

ダウンロードした、python-2.7.8.msi を実行するとインストーラーが起動して、ウィザードに従ってインストール（アップデート）します。以前のバージョンが削除されるというメッセージがでてインストールされていたバージョンが削除され2.7.8がインストールされます。

pandas：Python Data Analysis Library　最新のバージョン0.14.1がリリース

　easy_install コマンドを使ってアップデートします。APIの拡張や変更が行われていてより使いやすくなっています。変更点や新機能に関しては、こちらをご覧ください。

C:\>easy_install -U pandas

IPython　最新のバージョン2.1.0がリリース

　easy_install コマンドを使ってアップデートします。2.0.0から多くのバグフィックスが適用されています。変更点についてはこちらをご覧ください。

C:\>easy_install -U ipython

その他のパッケージ

　xlrdやpatsyもそれぞれ最新版がリリースされていますのでeasy_install コマンドを使ってアップデートしておきましょう。

C:\>easy_install -U xlrd
C:\>easy_install -U patsy