時系列分析II―ARMAモデル（自己回帰移動平均モデル）の評価と将来予測：ITエンジニアのためのデータサイエンティスト養成講座（10）（4/4 ページ）

過去の時系列データを基に、将来予測につながるモデルを検討、実際に将来予測を行って検証してみましょう。

[中林紀彦，日本アイ・ビー・エム]

検証したモデルを使って未来を予測する方法

　では、最後にできたモデルを使って未来の予測を行ってみましょう。モデルを作成するのに用いたのは2013年末までのデータでしたので、それ以降の値をモデルを使って予測し実測値と比較してみましょう（In [66]〜In [68]）。

In [65]: # 2014年1月から2015年12月までの予測
In [66]: dfm.plot()
Out[66]: <matplotlib.axes.AxesSubplot at 0x8124930>
In [67]: arma_mod1201.predict(119, 143, dynamic=True)
Out[67]:
2013-12-31     20.177125
2014-01-31     18.617049
2014-02-28     20.818746
2014-03-31     42.647924
2014-04-30     33.622861
2014-05-31     59.955508
2014-06-30    142.005617
2014-07-31    272.722329
2014-08-31    248.655620
2014-09-30     70.135271
2014-10-31     23.449048
2014-11-30     18.595086
2014-12-31     17.501989
2015-01-31     15.618556
2015-02-28     21.293898
2015-03-31     38.488424
2015-04-30     31.562623
2015-05-31     58.783273
2015-06-30    142.198106
2015-07-31    265.198532
2015-08-31    231.481480
2015-09-30     72.762567
2015-10-31     23.619889
2015-11-30     17.579656
2015-12-31     15.881682
Freq: M, dtype: float64
In [68]: arma_mod1201.predict(119, 143, dynamic=True).plot(style='r--')
Out[68]: <matplotlib.axes.AxesSubplot at 0x8124930>

　最初に実際のデータをプロットしておきます（In[66]）。次にモデルを使った予測を行います。predictメソッドを使い、まずは値を確認します（In[67]）。引数の119および143は、実データの最初の月である2004年1月から数えて119カ月目（2013年12月）と143カ月目（2015年12月）ということを表しています。

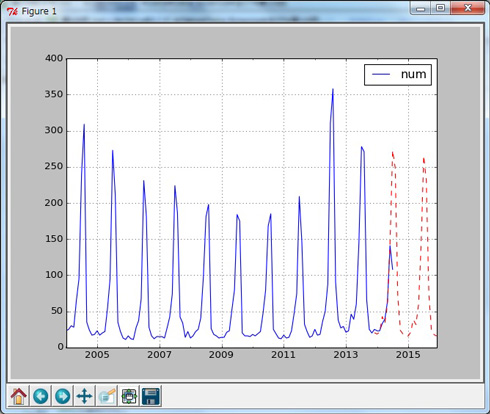
　値の確認ができたところで、先ほどのプロットに予測値を重ねてみます（In[68]、図5）。

　図5を見て分かるように2014年1月から6月までかなり実測値に近い予測ができています。この結果から、ARMA(13,0)モデルは「夏休み」というキーワードの検索数を予測する場合のみ、かなり精度の高いモデルだということができます（2014年7月はデータが途中なので比較していません）。

図5　ARMA(13)モデルの残差の自己相関、偏自己相関

おわりに

　前回と今回の2回にわたって時系列分析について、ARMAモデルを中心に紹介してきましたが、前回紹介したように、時系列分析はデータ分析の中では比較的歴史のあるテーマであり、さまざまなモデルが提案されていますので機会があればARMAモデル以外のモデルにも挑戦してみてください。

　次回は“おむつとビール”の例えで有名な買い物かごの分析であるアソシエーション分析について紹介します。

　アソシエーション分析についての理論を簡単に説明し、実際にサンプルデータを使った具体的な方法を解説します。お楽しみに。