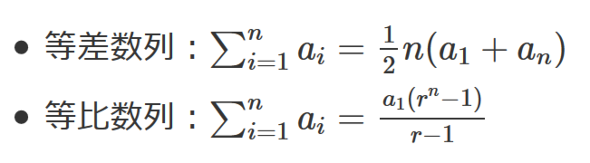数学、統計学を学ぶ上で必須となる「集合・数列」の6つの数学記号をPythonコードと図で理解する：「AI」エンジニアになるための「基礎数学」再入門（6）（2/2 ページ）

AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す連載。今回は数学、統計学を学ぶ上で必須となる「集合・数列」の数学記号についてPythonコードと図を交えて解説します。

[西村圭介，東京ITスクール]

数列とは？

　数列とは、その名の通り数字が列をなしているもののことを指します。

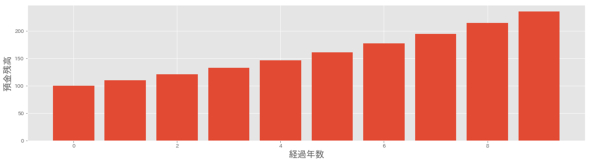
　まずは、身近な例で考えてみましょう。年利が10％の銀行口座に100万円を預け、1年、2年……とたつと、次のように預金残高が変化していきます。

図5　預金残高の推移

　この数字の羅列を式で定義するならば、次のように記述します。

　数列{a_n}を「a_n=100(1+0.1)ⁿ」と定義する。

　nに0、1、2、……と代入していくと、上の数列が再現できることが分かると思います。以下のPythonスクリプトを動かして、ぜひ確認してみてください。

import japanize_matplotlib
import matplotlib.pyplot as plt
plt.style.use('ggplot')
 
def deposit(n):
    return 100*(1.1**n)
 
y = [i for i in range(9)]
deps = [deposit(i) for i in y]
 
plt.bar(x=y, height=deps)
plt.xlabel("経過年数")
plt.ylabel("預金残高")
 
plt.show()

　なお、数列には例として次のような特殊なものがあります。

• 等差数列：n番目とn+1番目の値の差が一定（1、3、5、……のような数列）
• 等比数列：n番目とn+1番目の値の比が一定（上のa_nは等比数列に該当する）

　これらの特殊な数列にはそれぞれの性質があるので、後で紹介します。

Σ：総和

　Σは「シグマ」と呼び、数列内の数値を合計することを示す記号です。Pythonや「Microsoft Excel」のsum関数に相当する記号です。連載第3回の記事でも紹介していますが、いま一度確認しておきましょう。使い方は次の通りです。

　ここでΣの上下に付いている文字は次のようなことを表しています。

• 上のn：「何項まで合計するか？」を表します。この例ではn項までと、一般化されている
• 下のi=1：「何項から合計するか？」を表します。この例では第1項（初項）から合計することを表している

※仮にこの2つの記述がなければ、「数列内の数値全てを合計する」というふうに解釈してください。

　試しに上で定義した{a_n}を第3項まで合計してみます。

　補足となりますが、等差数列や等比数列の合計値には公式が存在します。

　これらの公式の証明などは割愛しますが、興味がある方は調べてみてください。

Π：総乗

　Πは「パイ」と呼びます。お気付きの方もいるかと思いますが、円周率を表す際によく用いる「π」の大文字です。これは数列内の数値の積を取ることを示す記号です。

　同様に第3項までの積を取ってみます。

　ΠはΣに比べると目にする機会が少なく、物怖じされがちな記号である印象があります。しかし、「幾何平均」「クロスエントロピー」と呼ばれる重要な指標を計算する際に用いられるので覚えておく必要があります。

　使い方はΣと同じなので難しくありません。違うのは「足し算ではなくかけ算である」点だけです。

ΠやΣを使った数式

算術平均（一般的にいう「平均値」）

　これも連載第3回で解説しましたが、いま一度紹介します。

　Σは算術平均以外でも分散など多くの場面で利用されます。

幾何平均

　説明に移る前に、まずは次のような表を想定しましょう。

日付	株価	前日比
1月1日	100	―
1月2日	120	1.2
1月3日	36	0.3
※前日比 ＝ 当日の株価 ÷ 前日の株価

　ここで、「前日比の平均を教えてください」と依頼されたとしましょう。

　単純に算術平均を計算すると、(1.2 ＋ 0.3) ÷ 2 ＝ 0.75となりますが、本当にこの「0.75」という値は「平均」と呼ぶのにふさわしいのでしょうか。試しに、1月1日の株価に0.75を2回かけてみます。

100 ⋅ 0.75² = 56.25

　なんと、1月3日の株価である「36」と乖離（かいり）してしまいました。これでは平均と呼ぶのにはふさわしくありません。

　ここで登場するのが、幾何平均です。次のように計算します。

　この場合だと、次のようになります。

　この0.6を1月1日の株価に2回かけてみます。

100 ⋅ 0.6² = 36

　今度は1月3日の株価と一致しました。よって、比の平均を取る場合は幾何平均を用いましょう。

　補足として、Pythonで幾何平均を計算するスクリプトの例を紹介しておきます。

def geometric_mean(X):
    n = len(X)
    pi = 1
    for x in X:
        pi *= x
    return pi**(1/n)
 
ratio = [1.2, 0.3]
 
geometric_mean(ratio)
# 結果: 0.6

次回は、分かっているようで分かっていない、数学における「関数」

　今回学んだ記号を一覧にしておさらいしておきましょう。

記号	読み	概要
∈	要素	「aは集合Aの要素である」ことを表す
⊆	部分集合	「集合Bは集合Aの部分集合（集合Aに包含されている）」ことを表す
∩	共通集合	「集合Aと集合Bの共通集合」を表す
∪	和集合	「集合Aと集合Bの和集合」を表す
Σ	シグマ（総和）	数列を合計することを示す
Π	パイ（総乗）	数列の積を取ることを示す

　これらの記号は、これから統計学および機械学習の分野の学習を進めるに当たって欠かせないものです。近々、「確率」について解説する予定ですが、そこでも用いるので、しっかり意味を理解した上で読んでいただければと思います。

　次回は、分かっているようで分かっていない、数学における「関数」について解説する予定です。ご期待ください。

筆者紹介

西村圭介

1991年、富山県生まれ。大学院を卒業し、企画コンサルタントとしてキャリアをスタートする。その後、統計学とプログラミングスキルの知見を基にデータサイエンティストとしてのキャリアを進める。現在は東京ITスクールの講師として、実務レベルのデータサイエンティスト輩出を目的としたAI研修に努める傍ら、分析や機械学習を用いたマーケティング支援を行う。