数学、統計学を学ぶ上で必須となる「集合・数列」の6つの数学記号をPythonコードと図で理解する：「AI」エンジニアになるための「基礎数学」再入門（6）（1/2 ページ）

AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す連載。今回は数学、統計学を学ぶ上で必須となる「集合・数列」の数学記号についてPythonコードと図を交えて解説します。

[西村圭介，東京ITスクール]

　AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す本連載『「AI」エンジニアになるための「基礎数学」再入門』。前回、前々回はデータ加工の部分の解説で、実務寄りの内容でした。今回は基礎や学術的な内容です。

　数学や統計学関連の文献を目にする際、以下のような記号を目にすることがあると思います。

• 集合関連
  • ∈：要素
  • ⊆：部分集合
  • ∩：共通集合
  • ∪：和集合
• 数列関連
  • Σ：シグマ（総和）
  • Π：パイ（総乗）

　これらの記号について、「いまいちどういうものか分かっていない」という方もいると思いますが、これらの理解なくしては数学、統計学を学んでいくことは困難です。

　そのため、今回のテーマである「集合・数列」を解説する目的は、「上記の記号の意味を理解すること」とします。

集合とは？

　集合とは、簡単にいえば「モノの集まり」です。モノは人、数字、果物など基本的には何でもよいのですが、それ以上分割できないモノ（これを「要素」といいます）である必要があります。つまり、要素が集まれば集合となるわけです。

　集合の例としては、下記のようなものがあります。

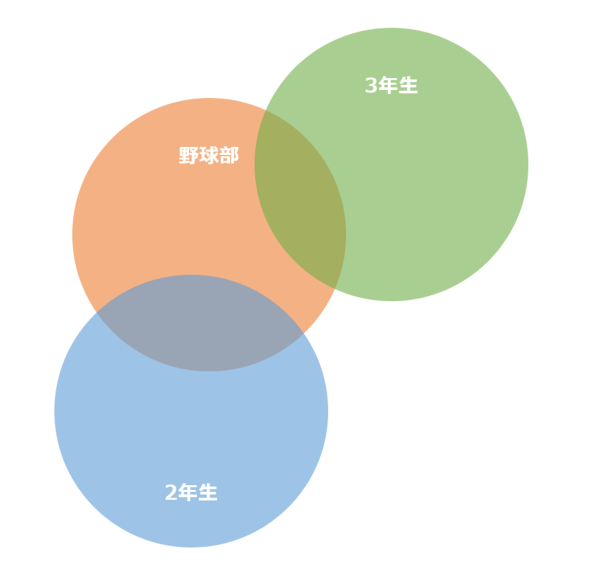
• ある高校の野球部の3年生（要素は、個別の人）
• 自然数：1、2、3……（要素は、個別の数字）
• かんきつ類（要素は、個別の果物）

　集合は他の集合とさまざまな関係性を持ちます。

　例えば「野球部は、3年生と2年生に共通の要素を持つが、3年生と2年生は共通の要素を持たない」という関係性があった場合、言葉では直感的には把握しにくいことがあります。

　こんなときに役立つのが「ベン図」と呼ばれる図式です。集合同士の関係性を簡潔に表してくれます。

図1　ベン図の例

　ここからは主要な関係性を幾つか紹介します。それらをベン図で直感的に確認しながら学んでいきましょう。

∈：要素

図2　要素の例

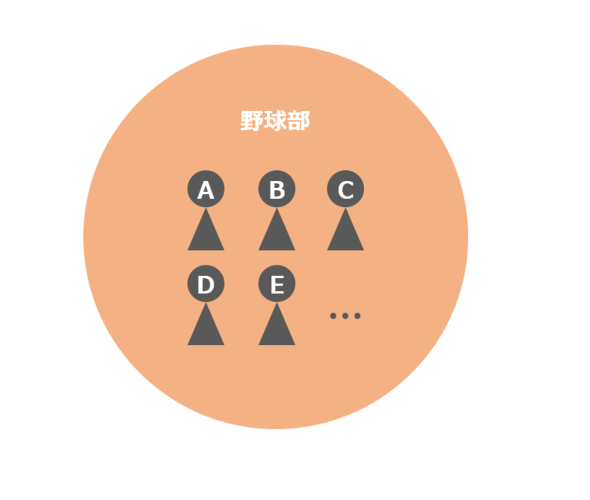
　図2のように「野球部」という集合がAさん、Bさん……といった要素で形成されていたとします。

　ここで「Aさんが野球部の要素である」ことを数式では次のように表します。

Aさん ∈ 野球部

　一方で、野球部ではないXさんがいたとします。つまりXさんは「野球部」という集合の要素ではありません。その場合は次のように表します。

Xさん ∉ 野球部

　この記号を用いた慣用的な記述として、このようなものをよく見掛けます。

• x ∈ N（xは自然数である）
• x ∈ Z（xは整数である）
• x ∈ R（xは実数である）

　これらの3つ集合（N：自然数、Z：整数、R：実数）は覚えておくといいでしょう。

⊆：部分集合

図3　部分集合の例

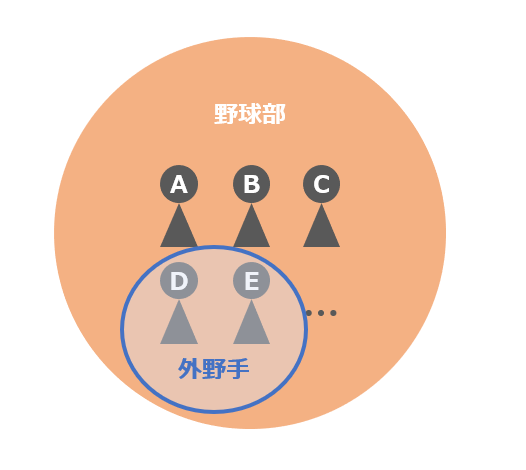
　図3は、「野球部」という集合の中に「外野手」という小さな集合が存在している様子を表したものです。これは「外野手は野球部の部分集合である」と表します。数式では次のように表します。

外野手 ⊆ 野球部

　先ほどの要素を表す記号とは非常に混同しやすいので、気を付けましょう。

集合演算子

　ここからは、集合が複数ある場合の関係性について確認します。

　まずは次のような集合を想定しておきましょう。

図4　共通集合、和集合の例

∩：共通集合

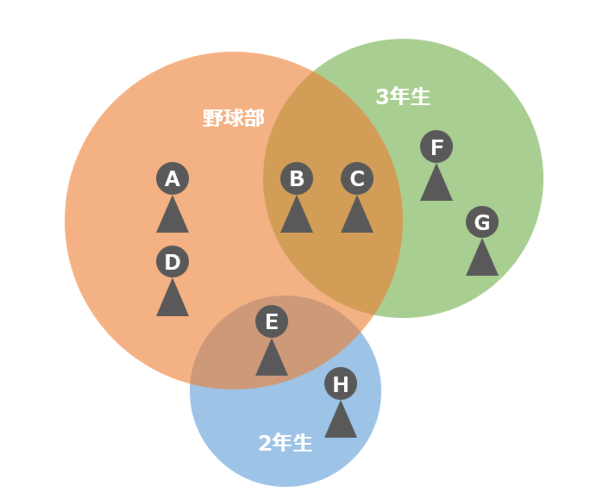
　図4では、BさんとCさんは「野球部かつ3年生である」ことが分かります。このBさんとCさんが属する集合は野球部と3年生の「共通集合」と表します。数式では、次のように表します。

野球部 ∩ 3年生

　なお共通集合は、Pythonでは次のように「&」で簡単に算出できます。

yakyu = {"A", "B", "C", "D", "E"}
third = {"B", "C", "F", "G"}
 
yakyu & third
# 出力: {'B', 'C'}

∪：和集合

　図4において、Hさん以外の全員が属する集合を定義するとしましょう。野球部の集合と3年生の集合を合わせれば、それが実現できそうです。言い表すならば、「野球部あるいは3年生である」ことを定義できればよいわけです。これは「∪」を用いることで定義できます。「和集合」とは、このように、集合と集合を合わせる（足す）ことを意味します。

野球部 ∪ 3年生

　和集合も、Pythonでは「|」で簡単に算出できます。

yakyu = {"A", "B", "C", "D", "E"}
third = {"B", "C", "F", "G"}
 
yakyu | third
# 出力: {'A', 'B', 'C', 'D', 'E', 'F', 'G'}

集合の応用

　自然言語解析の場面で、集合の考え方を応用することがあります。例えば、とある文章同士の類似度を求めたい場合に、下記のような数値を計算することがあります。

※AやBは各文章に登場する単語の集合を仮定しています。
※「|」記号は「要素数」を表します。例えば、Aの5つの要素で構成された集合ならば、「|A|=5」となります。

　Pythonコードで計算してみましょう。今回は、次の3つの文章を用意しました。

• A：Mary had a little lamb
• B：Little lamb little lamb
• C：Everywhere that Mary went

　それぞれの計算方法でAB間、AC間、BC間の類似度を求めてみます。

def jaccard(subs_l, subs_r):
    intersection = subs_l & subs_r
    union = subs_l | subs_r
    return len(intersection) / len(union)
 
def dice(subs_l, subs_r):
    intersection = subs_l & subs_r
    return 2*len(intersection) / (len(subs_l) + len(subs_r))
 
def simpson(subs_l, subs_r):
    intersection = subs_l & subs_r
    return len(intersection) / min(len(subs_l), len(subs_r))
 
A = "Mary had a little lamb"
B = "Little lamb little lamb"
C = "Everywhere that Mary went"
 
subs_A = set(A.split(" "))
subs_B = set(B.split(" "))
subs_C = set(C.split(" "))
 
# 例: AとBのJaccard係数
jaccard(subs_A, subs_B)
# 出力: 0.3333333333333333

　結果は次のようになりました。

計算対象	Jaccard係数	Dice係数	Simpson係数
AB間	0.333	0.5	0.666
AC間	0.125	0.222	0.25
BC間	0.0	0.0	0.0

　どの指標も計算方法は違えど、同じ単語が出てくる文章同士の値は大きくなる傾向を確認できました。

　なお、これらの指標は文章間の類似度以外でも、購入商品のログを用いてユーザー間の趣味嗜好の類似度にも応用できます。