昔は弾道計算、今はAIモデルのパラメーター算出に重要な「微分・積分」:「AI」エンジニアになるための「基礎数学」再入門(8)(1/2 ページ)
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す連載。今回は数学、AIがデータとの最適な対応関係を見つけるのに重要となる「微分・積分」についてPythonコードと図を交えて解説します。
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す本連載『「AI」エンジニアになるための「基礎数学」再入門』。前回は、「関数」について解説し、「関数とはデータ間の対応関係を定量的に表したもので、AIはデータ間に存在するこの対応関係を数値的に見つけ出すことである」と説明しました。今回は関数の性質を深く知り、AIがデータとの最適な対応関係を見つけるのに重要となる「微分・積分」について解説します。
微分・積分の考え方
数学でよく聞く微分・積分の基本定理は昔のヨーロッパで発見されました。最初に微分・積分の本質について説明すると、微分は「関数の傾き」を求める方法で、積分は「関数の面積」を求める方法です。どちらも関数が持つ情報を取り出すための方法であり、特に微分はAIが行うデータ解析においてよく利用されています。
微分・積分が発見された時代、「砲弾の弾道を計算したい」というニーズがありました。大砲から発射された砲弾は重力に従って刻々と進行方向が変わるため、その運動を正確に計算することができませんでした。砲弾の速度を時間の関数として扱い、微分・積分を用いると、このような「変化する運動の振る舞い」を知ることができ、砲弾の最高到達地点などを計算から推測できます。現代でも微分・積分による恩恵は日常生活の中にもあり、例えば車の速度メーターが出す現時点での速度は微分を用いて計算されています。
微分で速さを求める
先ほど説明した通り微分・積分は関数の性質(傾きや面積)を知るための重要な手法であり、数学でも重要な部分なので多くの解説では数学記号を用いてその導出などを一般的な関数に対して説明しています。しかし、分かりやすさのため、ここでは微分・積分の概念について数学記号などをあまり使わずに現実的な比喩を用いて説明していきます。
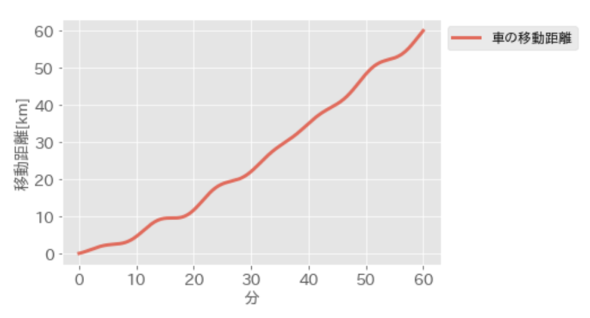
例として、ある車の移動距離からその車の速さを求める問題を考えます。前回説明した関数の知識を用いると、車の移動距離が「時間の関数」として表されることになります。この関数をグラフで表すと、下記のような時間(分)とその移動距離(km)の図が得られます。図から60分で60キロ移動していることが分かります。ではこの車は平均的にどのくらいの速さ(km/分)で移動したのでしょうか?
速さとは移動距離の時間変化量なので、移動距離とその時間が与えられたとき、速さは下記の公式で得られます。
速さ = 移動距離 ÷ 時間
図1から、車の移動距離が直線ではないので、車の速さは一定ではないこと、60分の時点で60キロに到達していることは分かります。よって、上記の関係式から車の平均速さは「60km/60分」となり、「1km/分」であることが求められます。データとこの関係式を知っていれば、平均的な速さは簡単に求めることができると思います。
現実で走る車は常にこの平均の速さで移動することはなく、速さは常に変化しています。では時間が30分の時点の速さを移動距離から知りたいときはどう求めればよいのでしょうか?
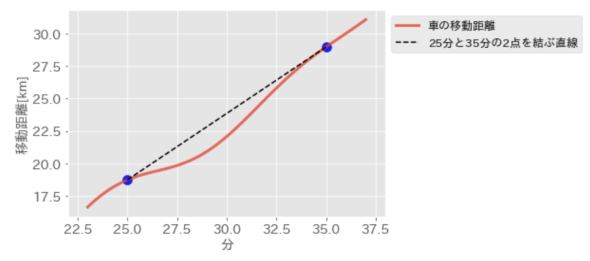
速さを求める時間の範囲を狭くして速さの式を用いれば、ある程度推測できそうです。図1を30分付近に拡大して見てみます。図2を見てください。
0〜60分の時間間隔よりも小さい25〜35分の10分間隔で速さを考えてみましょう。25分時点での移動距離は18.73キロであり、35分時点では28.97キロでした。この時間間隔に速さの式を適応すると、以下のようにこの区間での速さが求められます。
(28.97km - 18.73km) ÷ (35分 - 25分) = 1.02 km/分
実はこの区間での平均の速さ(1.02km/分)は上記2点を通る直線の傾きと同じであり、図の点線はこの平均の速さ(傾き)で移動した場合の移動距離を表しています。60分の期間を使用した場合よりは正確な速さが求められましたが、あくまでの30分付近の10分間を用いた平均的な速さであり、30分時点での速さではありません。点線と実線に乖離(かいり)があることからも、このとこが分かります。しかし、考える時間の範囲を十分短くして微小な移動距離の変化量を求めれば、30分付近の速さに近づけることができます。つまり、ある瞬間の速さは下記で求めることができます。
瞬間の速さ(瞬間の移動距離の傾き) = 微小な移動距離 ÷ 微小な時間
この微小な区間での変化量(傾き)を求めることが、微分です。厳密には微小な時間間隔を0まで小さくしたときに、30分時点での速さ(傾き)が求まりますが、数値計算では分母を完全な0にすることができないので、微小な時間として十分短い間隔の値を用いて傾きを求めています。このように微分は関数の瞬間ごとの傾きを求めることに使用されます。つまり微分とは対象の関数(今だと移動距離)の傾きを求める方法といえます。
例として時間を用いたので、「瞬間ごとの傾き」という表現を使っていますが、時間の関数以外でも微分は計算できます。例えば、消費カロリーが体重の減少量の関数として与えられた場合は、消費カロリーにおける体重減少の傾きが微分で得られます。
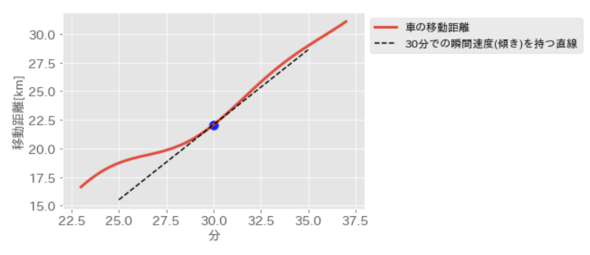
微小な区間で30分付近の速さ(移動距離の傾き)を求めたものが図3です。30分付近での移動距離の傾き(移動距離の変化量)と微分で求めた傾きを持つ直線が極短い範囲で一致していることが分かります。
関数の傾きが分かると多くの利点があります。
ある時点での傾きが分かると次の瞬間に進む(関数が上がるのか下がるのか)方向や、その大きさがある程度推測(傾きから得られるのは直線なので、直線での推測になる)できます。現実の問題では関数全体の振る舞い(関数の全体図)が分からないことが多いので、関数の次に進む方向がある程度分かるのは大きな利点です。
また、関数の傾きを求めることで関数の振る舞いを深く知ることができます。傾きが大きいときは関数の変化は大きく、傾きが小さいときは関数の変化も小さくなります。移動距離で例えると、「傾きが0になった場合、速さが0になる」ということなので、その時点での移動距離は変化しないことが分かります。
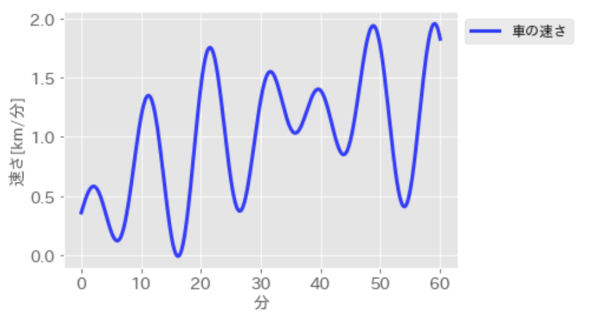
では、この移動距離の全ての瞬間ごとに速さ(傾き)を求めてみましょう。その結果が図4です。微分を用いたことで、時間の関数だった移動距離のデータから速さが時間の関数として得られました。速さを時間の関数として得られたことで、移動時間内で車がどんな運動をしたかを把握することができます。図を見ると16分辺りで車の速さは最小となり、49分辺りで速さは最大となっていることが分かります。
Pythonのコードでも微分を行ってみましょう。微分を計算するときの間隔を変化させて結果がどう変わるかを以下のスクリプトを実行して確認してみてください。間隔の幅を小さくするごとに微分の結果がある値に収束していき、正確な傾きが求められていることが分かります。
# ある2次関数の結果を返す関数の定義
def func_1(x):
return 1*x*x + 3*x
# 微分を計算する関数の定義
def diff_func(x,dx):
return (func_1(x+dx) - func_1(x))/dx
# x = 3での微分結果を微小区間dxの大きさを変えて結果を出力する
for dx in [1,0.5,0.3,0.1,0.01,0.001]:
print('微小区間の幅 =',dx,'微分結果 = ',diff_func(3,dx))
微小区間の幅 = 1 微分結果 = 10.0 微小区間の幅 = 0.5 微分結果 = 9.5 微小区間の幅 = 0.3 微分結果 = 9.299999999999997 微小区間の幅 = 0.1 微分結果 = 9.100000000000037 微小区間の幅 = 0.01 微分結果 = 9.009999999999962 微小区間の幅 = 0.001 微分結果 = 9.000999999997816
積分で移動距離を求める
微分について説明したので、次は積分に移ります。
積分は微分の逆の考え方であり、微分が関数の傾きを求めるなら積分は関数の面積を求める方法です。関数の面積を求めることがなぜ微分の逆であり、何を意味するのでしょうか? 先ほどの速さのグラフを例にとって解説します。
前回は最初に車の移動距離が時間の関数として得られている場合を考えましたが、今回は最初に車の速さが時間の関数として与えられた場合を考えます。時間によって刻々と変化する速さのデータからある瞬間までの移動距離を求めたい場合に積分が使われます。
移動距離と時間を用いて速さが下記の関係式で表されます。
速さ = 移動距離 ÷ 時間
そのため、移動距離は次のように求めることができます。
移動距離 = 速さ × 時間
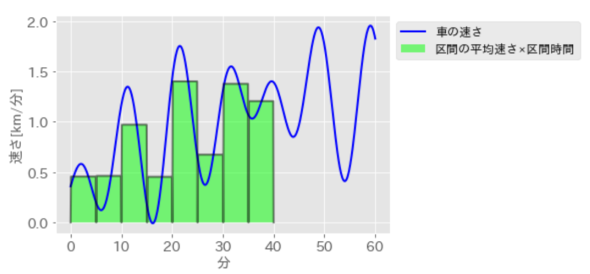
つまり、移動距離は速さと時間のかけ算(速さと時間の面積)で表すことができます。微分と同じように考えて、短い時間の間隔とその時間間隔での平均の速さを使えば、その区間での移動距離が求められます。40分を8で割った5分間隔ごとに分割し、その区間ごとの平均の速さと区間時間(5分)から移動距離を計算した結果が図5です。
速さの変化のスピードが5分より大きいため、この分割数である5分間隔ごとの面積(平均の速さと時間のかけ算)を足し合わせたものでは移動距離を表すことができていません。ですが、先ほどと同じように分割数を多くして間隔をどんどん狭くしていけば、その区間での正確な瞬間ごとの移動距離が計算できます。つまり、ある瞬間での移動距離は下記で求めることができます。
瞬間の移動距離(瞬間の速さの面積) = 微小な間隔での平均速さ × 微小な時間
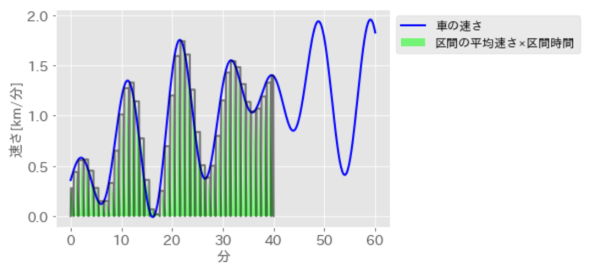
先ほどの5分よりさらに分割数を多くして区間の最小分割幅が1分ごとの移動距離を計算し、プロットしたのが、図6です。瞬間ごとの面積は5分間隔よりも小さくなったため、それぞれが表す区間ごとの移動距離は速さの変化の影響を表せるようになっています。
そして、これらの移動距離をある時刻まで足し合わせたものが、その時刻での移動距離です。時間間隔をさらに細かくして瞬間ごとの移動距離(面積)を計算し、その瞬間まで足し合わせることで速さのデータから図1と同じ車の移動距離のデータを再現できます。つまり積分とは対象の関数(今だと速さ)の面積を求める方法といえます。
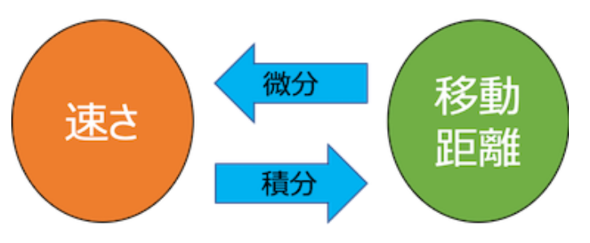
また、微分と積分の関係を移動距離と速さで考えると図7のようになっています。
つまり、積分は微分の逆の作用であり、微分したものを戻すことができます。微分もまた同じです。
積分もPythonのコードでその計算を行ってみましょう。積分を計算するときの間隔の分割数を変化させて結果がどう変わるかを以下のスクリプトを実行して確認してみてください。分割数を大きくなるごとに積分の結果がある値に収束していき、正確な関数の面積が求められていることが分かります。
import numpy as np # 数値計算用のPythonライブラリを読み込む
# ある1次関数の結果を返す関数の定義
def func_2(x):
return 2*x + 3
# 積分を計算する関数の定義
def inte_func(start_x,end_x,N):
S = 0.
# start_xからend_xまでの区間を等間隔でNに分割する
X = np.linspace(start_x,end_x,N)
# 分割後の微小区間の大きさ
dx = X[1] - X[0]
for x in X:
# 微小区間での平均値の代わりとして、微小区間(x,x+dx)での中央の値を用いる
S += func_2(x+dx*0.5)*dx
return S
# 0から3までの積分結果を区間の分割数の大きさを変えて結果を出力する
for N in [2,5,10,100,1000,10000]:
print('区間分割数 =',N,'積分結果 = ',inte_func(0,3,N))
区間分割数 = 2 積分結果 = 54.0 区間分割数 = 5 積分結果 = 25.3125 区間分割数 = 10 積分結果 = 21.11111111111111 区間分割数 = 100 積分結果 = 18.273645546372823 区間分割数 = 1000 積分結果 = 18.02703604505406 区間分割数 = 10000 積分結果 = 18.002700360045008
ここまで微分・積分について解説しました。それぞれ何を行っているか分かったと思います。次ページではAIが何の関数に微分を用いて、何を求めているかについて説明します。
Copyright © ITmedia, Inc. All Rights Reserved.
関連記事
 数学ができると「数学ができないエンジニアはダメだ」の効果が計れる
数学ができると「数学ができないエンジニアはダメだ」の効果が計れる
数学ができるとエンジニアとして活躍できるのか、むしろ数学ができないとエンジニア失格なのか?――「エンジニアに数学の知識は必要か?」を、数学オタクが論理的に解説します。 AI・機械学習のための数学超入門 ― 前提知識は四則演算だけ!
AI・機械学習のための数学超入門 ― 前提知識は四則演算だけ!
機械学習の数学は難しい!? そう思っている人はここから学んでみよう。本連載では、小学校で習う「四則演算(足し算/引き算/掛け算/割り算)」を使って、機械学習の数学をできるだけ分かりやすく簡単に説明していく。だからサブタイトルは「― 中学/高校数学のキホンから学べる」。今回は距離を求める中学数学をおさらいする。![[Python入門]Pythonってどんな言語なの?](https://image.itmedia.co.jp/ait/articles/1904/02/news024.gif) [Python入門]Pythonってどんな言語なの?
[Python入門]Pythonってどんな言語なの?
機械学習に取り組んでみたいという人に(そうでない人にも)向けて、Pythonプログラミングを基礎からやさしく解説する連載をPython 3.10に合わせて改訂します。