回帰分析I：回帰分析って何？ から、最小二乗法、モデル評価、妥当性検討の実際まで：ITエンジニアのためのデータサイエンティスト養成講座（6）（1/3 ページ）

今回は回帰分析の実施方法や仮説を基にしたモデルの検証、妥当性検討の手法について解説します。実際の例を基に手を動かして学習していきましょう。

[中林紀彦，日本アイ・ビー・エム]

連載バックナンバー

はじめに

　前回は代表的な4つの基本的な分析手法についてご紹介しました。今回はその中の「回帰分析（Regression Analysis）」について、より詳しく説明し、実際のデータを使って回帰分析を行ってみたいと思います。

回帰分析とは？

　回帰分析を説明する際に身長と体重を関係を分析する例がよく用いられます。体重は身長に比例するという仮説を立てると、前回紹介したように、

y＝ax＋b

というモデルを作ることができます。これに従うと今回は、

[体重]＝[身長]×[係数a]＋[定数b]

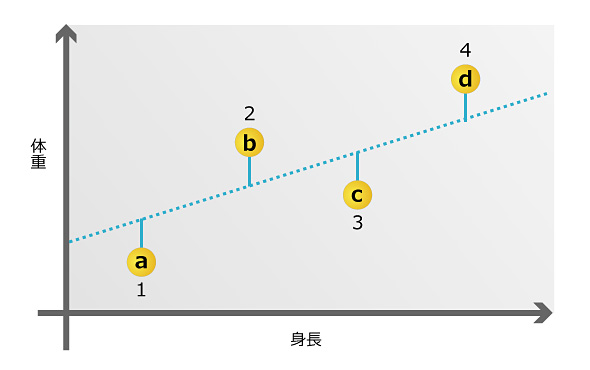
　というモデルを作ることになりますが、データを分析してこの“係数a”と“定数b”を求めてモデルを完成させるのが回帰分析です。一般的な回帰分析の場合、最小二乗法（OLS：Ordinary Least Squares）という方法を用いて、係数aと定数bを求めます。最小二乗法とは図1にあるように、例えば1から4のデータがあるときに、[a, b, c, d]それぞれの2乗を足したものが最小になるような傾きと切片を持つ直線を求める方法です。

図1　最小二乗法のグラフ（例）

　具体的な解法はこちら（リンク）にも載っています。今回はアルゴリズムを作って計算することはありませんが、どのような方法で導かれているのかは一度目を通しておくとよいでしょう。

実際の身長と体重の関係は？

　では実際にPythonを使って身長と体重の関係を回帰分析してみましょう。

　身長と体重のデータはダミーデータではなく一般社団法人人間生活工学研究センターが公開している「子どもの身体寸法データベース」にある実データを使いましょう。こちら（リンク）で公開されている圧縮ファイル（リンク：zipファイル）をあらかじめダウンロードして解凍しておきます。なお、データの利用に当たっての注意事項（リンク）がありますのでよく読んでから利用するようにしましょう。

手順1：データを準備して視覚化し全体像をつかむ

　まず、いつものように（バックナンバー参照）CSVファイルをデータフレームに読み込みます（In [3]）。

　CSVファイルのヘッダーをそのまま利用するのは難しいので、ヘッダ部分の2行はスキップして3行目のデータからを読み込むようにし、headerパラメータを-1としてファイルからヘッダーを読み込まないように指定します。このデータは身長体重以外にも体のサイズに関する多くの項目が含まれていますが、今回は身長と体重のデータがある10列目と11列目のみを抽出して（In [6]、In [7]）使用します。その際にデータが欠けている行は事前に削除しておきます（In [4]、In [5]）。

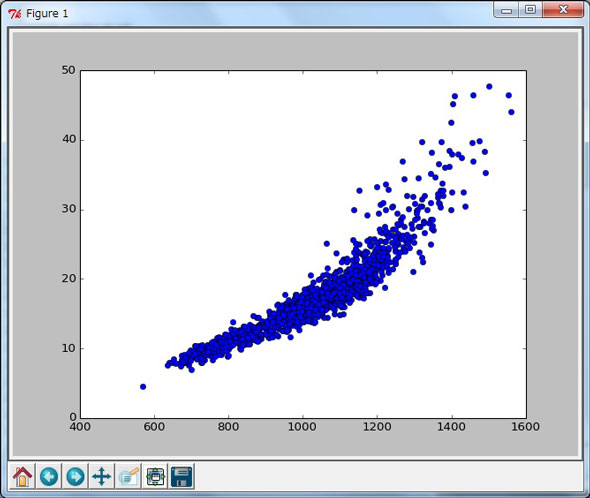
　実際の身長と体重の関係がどんな風になっているのかグラフで可視化して確認してみましょう（In [8]）。

In [1]: import pandas as pd
In [2]: import numpy as np
In [3]: df = pd.read_csv('children_data2005_08_130819.csv', header=-1, skiprows=2, encoding='Shift_JIS')
In [4]: df = df[np.isfinite(df[9])]
In [5]: df = df[np.isfinite(df[10])]
In [6]: height = df[9]
In [7]: weight = df[10]
In [8]: plot(height, weight, 'bo')
Out[8]: [<matplotlib.lines.Line2D at 0x46df0d0>]

グラフ1

手順2：モデル化：仮説を立てる

　グラフ1を見ると、微妙に曲がっているような気もしますが、ある程度直線とみなすこともできますので、まずは体重は身長に線形に比例するという最初の仮定に基づいてモデル化します。

[体重]＝[身長]×[係数a]＋[定数b]　―ー　モデル（1）