富山県民を分類してみたら……？――クラスタリング分析の手法：ITエンジニアのためのデータサイエンティスト養成講座（8）（1/4 ページ）

あるグループを属性ごとに分類する「クラスタリング分析」の基本を学ぼう。今回も自治体が公開しているオープンデータを題材にします。

[中林紀彦，日本アイ・ビー・エム]

連載バックナンバー

はじめに

　前々回、前回と2回にわたって代表的な4つの基本分析手法である回帰分析について紹介しました。今回はデータを幾つかグループに分類するための手法であるクラスタリング分析（Clustering Analysis）について詳しく説明したいと思います。

クラスタリング分析（Clustering Analysis）

　クラスタリング分析は、購買金額や頻度などの属性から顧客データなどをグループに分類する手法で、分類方法は大きく分けて、階層的に分類する手法と分類数（クラスタ数）を決めて分類する非階層的手法の2つのアルゴリズムがあります。

　分類する対象が多い場合には、あらかじめ分類する数を決めておくことができる非階層的手法が用いられるケースが多いので、今回は非階層的手法を用いたクラスタリング分析についてご紹介していきたいと思います。

非階層的手法―K平均法（k-means clustering）

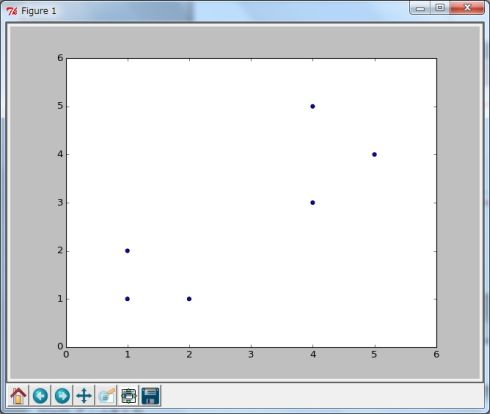
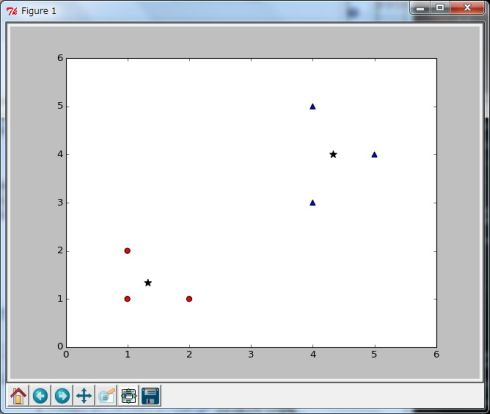
　非階層的手法の中でも、シンプルで広く用いられている手法がK平均法（k-means clustering）（Wikipediaの解説）です。まずは説明を簡単にするために2次元のデータ（図1）を使ってアルゴリズムを説明します。

図1　サンプルの2次元データ

K平均法のアルゴリズム

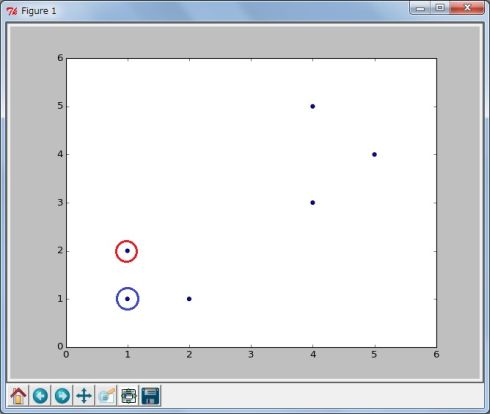
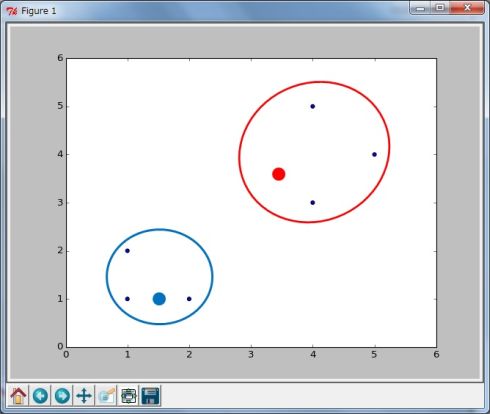
（1）初期値、クラスターの中心点を決める　6つのデータを2つのクラスターに分割するために、ランダムにクラスターの中心点を決めます（図2）。この例では分かりやすくするために、左下2つのデータを中心点の初期値としています。

図2

（2）残り4つを分類　残りの4つを、2つの中心点からの距離を比較して近い方のクラスターに分類します（図3）。

図3

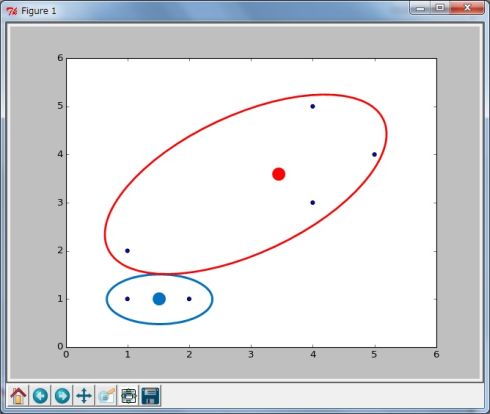
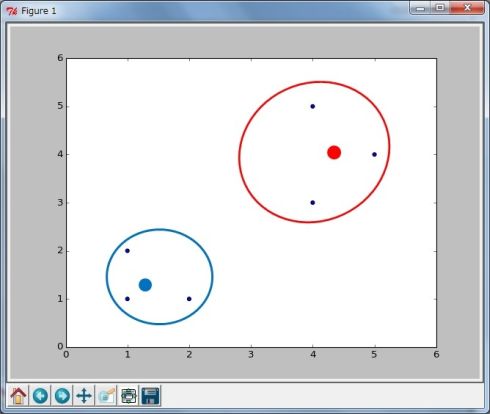
（3）各クラスターの平均から新しい中心点を求める　それぞれのクラスターに含まれるデータの算術平均を計算して、新しい中心点とします（図4）。

図4

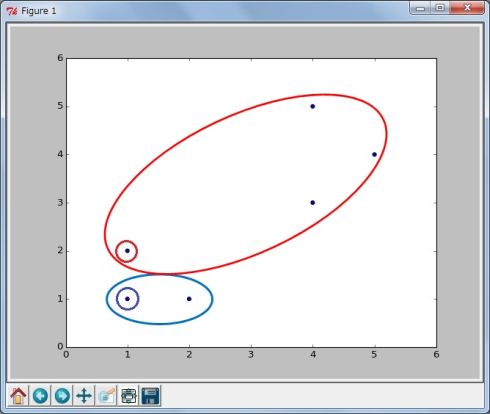
（4）クラスター分類を補正　6つのデータの座標を、新しい2つの中心点からの距離を比較して近い方のクラスターに分類します（図5）。

図5

（5）新しい中心点を求める　再度、それぞれのクラスターに含まれるデータの算術平均を計算して、新しい中心点とします（図6）。

図6

（6）クラスター分類を補正、収束するまで行う　再度、中心点からの距離を比較して近い方のクラスターに分類します。このケースではクラスターの割り当てに変化がないため収束したと判断して計算を終了します（図7）。

図7

　収束条件は、変化量がしきい値を下回る場合や、繰り返しの回数を設定する方法なども用いられます。