メールアドレスを公開鍵にする――「ペアリング」とその応用例:クラウド時代の暗号化技術論(5)(2/2 ページ)
「好きな文字列を公開鍵として使いたい」「情報を暗号化したまま復号できる人を変更したい」――第5回では、暗号に対して求められるこのような利便性を達成するための技術である「IDベース暗号」「代理人再暗号化」と、その基礎となる「ペアリング」という関数について解説します。
ペアリングを使ったID鍵共有
ペアリングについての説明をしたところで、1999年に大岸氏らが提案したペアリングを使ったID鍵共有方式を紹介しましょう。これは以下のようなアルゴリズムからなります。
セットアップ
鍵生成局が、楕円曲線Eとハッシュ関数を用いてIDを楕円曲線上の点として表現する手順を決めておく。ユーザーXのIDをPX∈Eとする。整数sをマスター秘密鍵とする。
秘密鍵の生成
生成局は各ユーザーXに対してKX=sPXを秘密鍵として渡す。
鍵共有
Aは秘密鍵KAと、BのID PBを使い、sA=e(KA,PB)を計算する。
Bは秘密鍵KBと、AのID PAを使い、sB=e(PA,KB)を計算する。
このとき、前節で説明したペアリングを用いると、
sA=e(sPA,PB)=e(PA,PB)s=e(PA,sPB)=sB
が成立するので、2人の間で秘密の値を共有できます。
楕円曲線を使った鍵共有(ECDH)とIDベースの鍵共有との比較表を以下に記します。ECDH鍵共有では秘密鍵を決めてから公開鍵が決まるのに対して、ID鍵共有では公開情報(ID)から秘密鍵が決まります。
| マスター鍵 | 自分の秘密鍵 | 相手の公開鍵(情報) | 共有鍵 | |
|---|---|---|---|---|
| ECDH鍵共有 | なし | a | bP | abP |
| ID鍵共有 | s | sPA | PB | e(PA,PB)s |
代理人再暗号化
IDベース暗号の次は、代理人再暗号化について紹介しましょう。例えば、顧客サポートを任されているAさんがクラウドに業務データを置いており、Aさんが休みの間はBさんやCさんが対応するとします。データを暗号化してクラウドに置く場合、従来なら秘密鍵をAさん、Bさん、Cさんの間で共有しなくてはなりません。しかし、鍵の共有は管理の面でいろいろ不安があります。
かといって秘密鍵を個別に持つとなると、Aさんは休みの前に一度データをダウンロードして復号し、Bさん、Cさんの公開鍵を使って再度暗号化してアップロードしなくてはなりません。これは手間と時間がかかります。
このとき、前回紹介した「準同型暗号」を使えば、原理的には暗号化したままデータを変換することが可能なのですが、前回も述べたように汎用的な準同型暗号は実現されたばかりでまだまだコストも高く、気軽に利用できないというのが実情です。
そこで、「暗号化されたデータを復号することなく別の人が復号できるようにする」という機能に対象を絞って、効率のよい方法を探す研究がなされています。
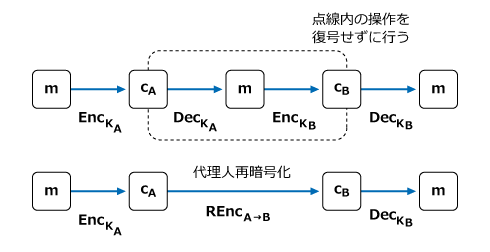
それが、「代理人再暗号化(PRE、Proxy Re-Encryption)」です。上述の通り、従来はAさんが暗号化した暗号文は、Aさん自身がいったん復号し、再度Bさん向けに暗号化し直す必要がありました。しかしPREを使えば、代理人(プロキシー)がBさん向けに再暗号化できるのです。
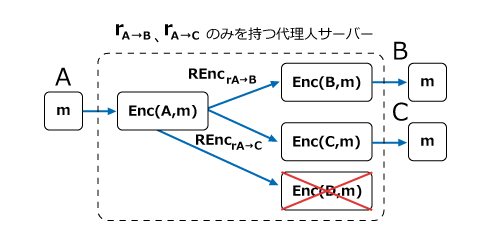
ここで重要なのは、代理人が無制限に再暗号化できるわけではなく、Aさんが許可した対象にだけ変換できる点です。例えば、AさんがBさん向けの変換を許可するときは、代理人に再暗号化鍵rA→Bを渡します。代理人はrA→Bを使うことで、Aさんの公開鍵で暗号化された暗号文を、Bさん向けに再暗号化できるのです。それ以外の人向けには再暗号化できません。もちろん、再暗号化鍵で復号を行うこともできません。
代理人再暗号化に関しては、2006 年にGiuseppe Ateniese氏らが、ペアリングを使った実用的な手法を提案しました。最近では第4回で紹介した格子暗号を利用するものや、ペアリングの代わりに電子署名と秘密分散を組み合わせた方式も提案されています。
ここで、ペアリングを使ったPREのキーアイデアを少し紹介しましょう。Aさんの公開鍵は前節の表1にもあるようにaPの形をしています。Bさんの公開鍵はbPです。代理人はaPをbPの形に変換したいのですが、そのためにはaPを(b/a)倍する必要があります。ところが、Aがこの値(b/a)を計算することはできません。Bの秘密鍵bが必要だからです。そこで代わりに、再暗号化鍵をrA→B=(1/a)(bP)とします。bPはBの公開鍵なので、AはrA→Bを計算できます。ここでペアリングを用いると、代理人はaPから、
e(rA→B,aP)=e((b/a)P,aP)=e(P,P)(b/a)a=e(P,P)b=e(P, bP)
とbPを含んだ形、すなわちBさんが復号できる形に変換できます。
他にもPREの応用例を紹介しておくと、2014年にNICTの王立華氏らが、IDベース暗号とPREを組み合わせた暗号システム「PRINCESS」を提案しています。これは機密レベルに応じてファイルの暗号化方法を変えて扱えるストレージサーバーです。
また、2014年から中央大学研究開発機構の辻井重男氏のユニットが、クラウド環境における機密情報の保護と利用の両立を目指した「組織暗号」という暗号方式の実証実験を行っています。辻井氏らのシステムは、例えば暗号文を総合受付に送信すると、担当部門の公開鍵を用いて再暗号化し、担当部門宛てに転送するといった機能を持っています。技術的には楕円ElGamal暗号と電子署名を組み合わせることで実現しているようです。
今回のまとめ
- 楕円曲線の2点で定まるペアリングは、暗号における重要な関数である。
- ペアリングを用いてIDベース暗号が構成される。
- 代理人再暗号化は、クラウド環境などのサーバー上で、情報を暗号化したまま復号先を変更できる技術である。
参考文献――より詳しく学びたい人のために:
IDベース暗号や代理人再暗号化についてより詳しく学びたい人のために、Web上で閲覧できるものや書籍として入手できる参考文献を紹介します。
IDベース暗号
- 『クラウドを支えるこれからの暗号技術』(光成滋生)
本連載の筆者による著書です。IDベース暗号、代理人再暗号化についても解説しています。 - 『(Web)IDベース暗号の概観と今後の展望』(金岡晃)
前半を読むことで、IDベース暗号の概略を知ることができるでしょう。 - 『(Web)IDベース暗号に関する調査報告書』(CRYPTREC IDベース暗号調査WG)
専門的な内容ですが、参考文献が豊富に紹介されています。 - 『暗号理論と楕円曲線』(辻井 重男・他)
- 『代数学から学ぶ暗号理論:整数論の基礎から楕円曲線暗号の実装まで』(宮地充子)
これらの2冊は専門書になります。意欲のある方は読んでみるとよいでしょう。
代理人再暗号化
- 『(Web)モジュール化に基づく高機能暗号の設計』(花岡悟一郎・他)
代理人再暗号化については、こちらの論文にその背景や必要性、解決すべき問題などが丁寧に書かれています。
- まだまだ広く深い、暗号の世界――匿名認証や電子投票に利用される「ブラインド署名」「グループ署名」「ゼロ知識証明」
- マイナンバーの漏えい対策にも利用される「検索可能暗号」とは――安全性と利便性の両立を目指す注目の暗号技術
- 動画配信サービスにも応用できる暗号とは――アクセス権を制御する「属性ベース暗号」
- メールアドレスを公開鍵にする――「ペアリング」とその応用例
- クラウドサービスに最適な暗号方式とは?――暗号化したまま計算する「準同型暗号」
- 鍵が漏れることも想定せよ――クラウド時代における「楕円曲線暗号」の必然性
- “安全な暗号”とは何か――「強秘匿性」「頑強性」という概念
- 重要なデータを守るため、もう一度暗号化技術をおさらいしよう
光成滋生(みつなり しげお)(サイボウズ・ラボ株式会社)
サイボウズ・ラボ株式会社にてセキュリティとインフラ周りの研究開発に携わる。「数論アルゴリズムとその応用」研究部会(JANT)幹事。
- 2004年放送型暗号の実装でIPA未踏スーパークリエータ認定
- 2005年ストリーム暗号Toyocryptの解読で情報化月間推進会議議長表彰
- 2010年ベクトル分解問題についての論文で電子情報通信学会論文賞受賞
- 2015年 Microsoft MVPアワード Developer Securityを受賞
近著に「応用数理ハンドブック」(朝倉書店、2013:楕円曲線暗号、ペアリング暗号の項目担当)、「クラウドを支えるこれからの暗号技術」(秀和システム、2015)がある。
Copyright © ITmedia, Inc. All Rights Reserved.