“安全な暗号”とは何か――「強秘匿性」「頑強性」という概念:クラウド時代の暗号化技術論(2)(1/2 ページ)
前回に引き続き、暗号化手法の一つ「ElGamal暗号」を学びます。そして攻撃に強く、「安全な暗号」に必要な要素とは何かを考えてみます。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
ElGamal暗号と強秘匿性
第1回で紹介したRSA暗号に続き、1984年に提案された公開鍵暗号「ElGamal暗号」を紹介します。
「ElGamal暗号」の考え方は、次回以降で紹介する楕円曲線暗号でも利用されます。これは次の方式で表現されます。
- 鍵生成:整数gと素数pを適切に選び、みんなに公開する(gとpの条件は省略します)。xをランダムに選びy=gx mod pとする。a mod bは整数aをbで割った余りを表す記号でした。以降mod pは省略します。
- 暗号化:公開鍵yを持つ人に対して平文mを送るには、整数rをランダムに選び、Enc(m)=(gr,myr)を暗号文とします。
- 復号:暗号文(c1, c2)=Enc(m) を受け取った人は自身の秘密鍵xを用いて、Dec(c1, c2)=c2/c1xで復号します。
ここで式の割り算a/bは、pで割った余りの中でうまく定義された演算を意味し、結果も整数になるものです。詳細は省略しますが、感覚的には普通の割り算と同じです(詳細は書籍「クラウドを支えるこれからの暗号技術」を参照ください)。
ElGamal暗号は、RSA暗号と違ってEncに乱数が入っているので「確率的アルゴリズム」です。
公開鍵暗号では、攻撃者が自由に選んだ平文に対する暗号文を作れるので、CPA(選択平文攻撃)に対して安全でなければなりませんでした。
暗号文から元の平文を求められないという性質を「一方向性」といいます。暗号には一方向性が備わっていなければなりませんが、第1回のネットオークションの例のように、平文のとり得る範囲が限定的であっても、暗号を破られては困るのでした。
極端な話、平文が「はい」か「いいえ」のどちらかであると攻撃者が知っている状況であっても、その暗号文がどちらの平文だったのか攻撃者に当てられてはいけないのです。
このような性質を「強秘匿性」(きょうひとくせい)といいます。
ElGamal暗号は(ある条件の元で)CPAに対して強秘匿性を持つことが知られています。RSA暗号では、「はい」を暗号化したかどうかは、自分で「はい」を暗号してみれば確認できたので、それに比べるとElGamal暗号はずっと安全なのです。
改ざんと頑強性
ElGamal暗号は強秘匿性を持っているのでとっても安全そうです。しかし、これもやはり使い方によっては安全ではないのです。
例えばAさんがBさんに、商品の代金m=1000円をElGamal暗号で暗号化して送ったとしましょう。AさんとBさんの間に攻撃者Cがいて、Enc(m)=(c1, c2)=(gr,myr)を盗聴し、(c1, 10c2)と改ざんしてBさんに渡します。
するとBさんは
Dec(c1, 10c2)=10myr / grx=10m
と復号してしまいます。1000円だったのが、1万円に変わってしまいました。
Cさんはもとの代金がいくらだったのかは分からないのですが、その値を10倍にすることはできるのです。これでは安心して使えませんね。このように第三者が暗号文から、その暗号文をいじって別の暗号文を作れては困ります。
そのようなことができない性質を「頑強性」(がんきょうせい)といいます。ElGamal暗号は頑強性を持っていないことが分かります。
Copyright © ITmedia, Inc. All Rights Reserved.

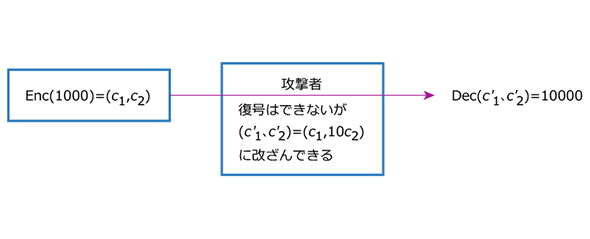 図1 ElGamal暗号に対する攻撃者による平文の改ざん
図1 ElGamal暗号に対する攻撃者による平文の改ざん



