第7回 回帰問題をディープラーニング(基本のDNN)で解こう:TensorFlow 2+Keras(tf.keras)入門
基本的なDNNの知識だけでも、さまざまな問題を解決できる。今回は「回帰問題」を解いてみよう。ディープラーニングの基本部分はワンパターンで、全く難しくないことが体感できるはずだ。
本連載では、第1回〜第3回で、ニューラルネットワークの仕組みと、TensorFlow 2.x(2.0以降)による基本的な実装コードを説明した。また、第4回〜第6回で、TensorFlow 2の書き方をまとめた。
これだけの知識を理解しただけでも、さまざまなニューラルネットワークを書けるようになっているはずなのだ。そこで今後の本連載では、より実践的な内容に入り、問題種別(回帰/分類)やニューラルネットワークモデル種別(CNN/RNN/GAN/BERT)といったさまざまな活用パターン(TensorFlow 2ベース)を紹介していく。
今回は、これまでに学んだ基礎知識を総合的に活用し、最も基本的な「回帰問題」をあらためて解いてみることにしよう。
なお、回帰問題と分類問題は、機械学習/ディープラーニングの基本的な問題種別である。今回第7回では「回帰問題」を、次回第8回では「分類問題」を取り扱う。と言っても難しくはない。重要なので繰り返すが、これまでの知識だけで、「基本的なディープ ニューラル ネットワーク」(以下、DNN)の実装が十分に、しかも自由に行えることを実感してほしい。
今回の内容と方針について
回帰問題とは?
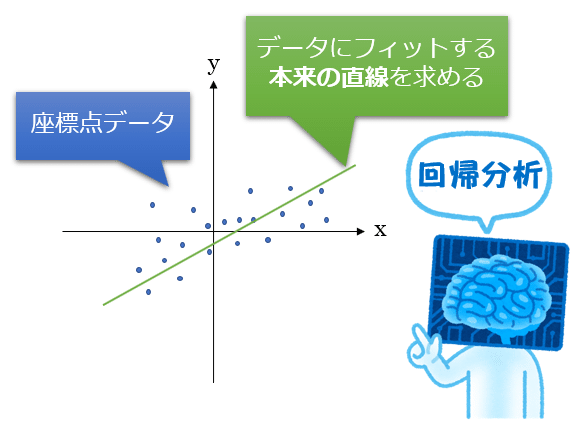
第1回では説明を割愛したので、今回あらためて「回帰」について簡単に説明しておこう。回帰(regression)とは、言葉の意味自体は「何らかの作用により再び元の状態に戻っていくこと」である。例えば「元の状態」が直線であるとしよう。XY座標系のグラフの中に複数の点データが存在し、その座標点データ群に最もフィット(=適合)する「本来の直線」(統計学的には回帰直線)を求めたいとする。このようなことを行う統計分析の手法を回帰分析(Regression analysis、特にここで仮定している分析手法はその一種である単回帰分析:Single regression analysis)などと呼ぶ(図1)。
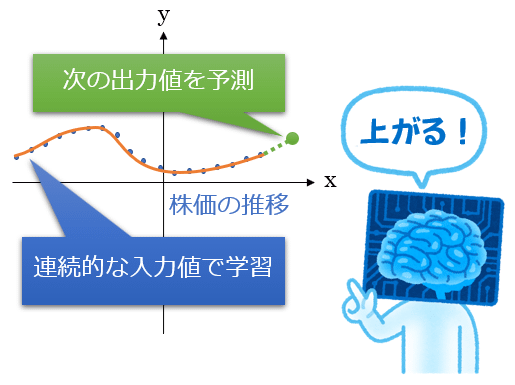
図1の回帰分析が示すように、「データ分析」では基本的に、過去に起きた物事が成立する要素や側面を明らかにすること(=既存の座標点データセットから回帰直線を求めること)に重きが置かれる。一方、「機械学習」は、未来に起きる物事を予測すること(=既存の座標点データセットでトレーニングした学習済みのモデルを使って、未知の座標点に対する結果を推論すること)が主目的である。もっと簡単に言うと、機械学習における「回帰問題」とは、「何らかの数値を未来予測すること」に他ならないのである。例えば「株価を予測する機械学習モデル」をイメージしてみてほしい(図2)。
株価は時系列データなので、図2のように、X軸を時間、Y軸を株価(終値など)にしたXY座標系のグラフを作成できる。このグラフに毎日の株価をプロットしていくわけだが、プロットされた座標点データ群は、3日前……2日前……昨日……今日(の株価)というように、連続したデータになっているはずである。連続データであれば、点と点をつないでいくことで1本の曲線が描けるだろう。この曲線にフィット(=適合)する数式(=数理モデル/機械学習モデル)が求まれば、明日の株価が機械的に予測できることになる。これが「回帰問題を解く」という意味である。
今回、取り扱う回帰問題について
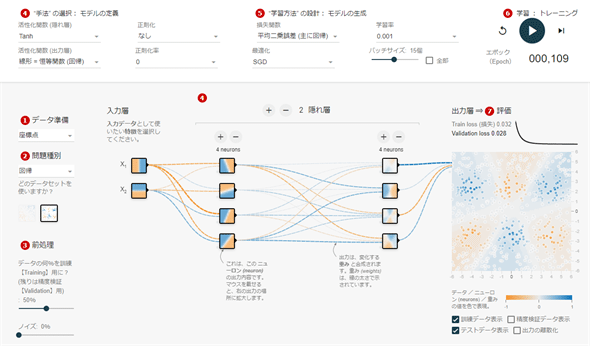
今回は、回帰問題を「ニューラルネットワーク Playground - Deep Insider」(以下、Playground)と同じデータセットを用いて解いてみることにしよう(図3)。以下を読み進める前に「Playgroundでは、回帰問題がどのように解けるのか」を直感的に確認したい場合には、上記のリンク先を開いて、右上にある[実行 ▷]ボタンを押して、挙動を確認してみるとよい。
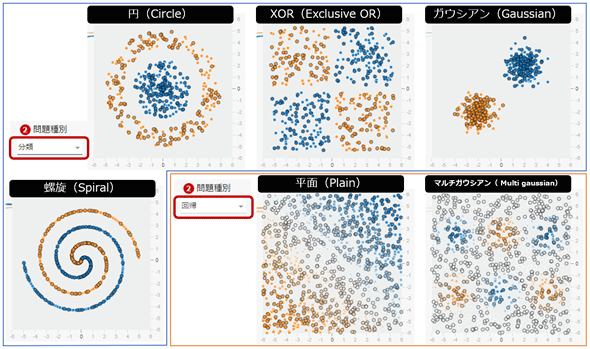
ちなみにPlaygroundでは、回帰問題として「平面(Plain)」と「マルチガウシアン(Multi gaussian)」の2種類が用意されている(図4)。
例えば「平面」の場合、左下の座標点(-6, -6)あたりが-1.0(=オレンジ色)で、右上の座標点(6, 6)あたりが1.0(=青色)に近くなっている。つまり、この回帰問題を解く場合は、任意の座標点を入力した場合に、-1.0〜1.0のような数値が予測できるようになればよいわけだ。例えば座標点(0, 0)に対する結果の数値を予測するなら0.0(白色)に近くなればよいし、座標点(-3, -3)の結果値を予測するなら-0.5(=ややオレンジ色)に近くなればよい。
「マルチガウシアン」の場合は、より複雑で、
- 左上が1.0(=青色)、中央上が-1.0(=オレンジ色)、右上が1.0(=青色)に近く
- 左下が-1.0(=オレンジ色)、中央下が1.0(=青色)、右下が-1.0(=オレンジ色)に近い
- さらに上記のように6分割した領域の中心部分は色が濃く(=1.0/-1.0に近い)、外縁部分になる従って色が薄い(=0.0に近い)
という特徴がある。この回帰問題をきれいに解くのは比較的難しいことは予想が付くだろう。今回は、この「マルチガウシアン」の座標点データセットを使用する。
今回、採用するTensorFlow 2の書き方について
第1回〜第3回ではSequentialモデルを使ったが、第5回でサブクラスモデル(Subclassing API)による書き方を学んだので、今回はサブクラスモデルで実装する。なお、学習/トレーニングの書き方は、応用的なカスタムループではなく、簡単に利用できるcompile()&fit()メソッドを利用することとする。
本稿で説明する大まかな流れ
基本的な実装の流れはワンパターンである。具体的には、以下の手順で実装していく。APIやコード内容の説明についてはこれまで(第1回〜第6回)の連載で十分に解説済みなので割愛し、特に注目してほしいポイントのみを取り上げていくことにする。
- (0)本ノートブックを実行するための事前準備
- (1)データの準備
- (2)モデルの定義
- (3)学習/最適化(オプティマイザ)
- (4)評価/精度検証
- (5)テスト/未知データによる評価
それでは、実際にTensorFlow 2を使って、この回帰問題を基本的なDNNだけで解いてみよう。自信があれば、ぜひ「どのようなコードを書けばよいか」、予想を立てながら、以降の記事を読み進めてみてほしい。それによって、自分の中に基礎力がきちんと身についているかを自己確認することもできるだろう。
(0)本ノートブックを実行するための事前準備
前提条件
今回は、Python(バージョン3.6)と、ディープラーニングのライブラリ「TensorFlow」の最新版2.2を利用する。また、開発環境にGoogle Colaboratory(以下、Colab)を用いる。
前提条件の準備は第1回など、これまでと同じなので、説明を省略する。詳しくはColabのノートブックを確認してほしい。
それでは準備が整ったとして、(1)から順に話を進めていこう。
(1)データの準備
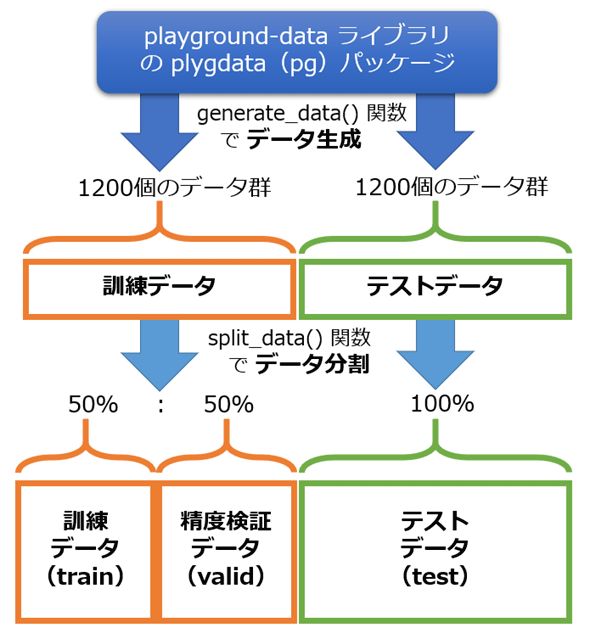
前述の通り、今回は「マルチガウシアン」の座標点データセットを用いる。このPlaygroundデータセットの生成には、(本連載独自の)ライブラリ「playground-data」が使える。まずはリスト1-1のようにして、playground-dataライブラリをインストールしてほしい。
# 座標点データセットを生成するライブラリのインストール
!pip install playground-data
playground-dataライブラリでは、リスト1-2のようなコードでデータを準備できる。なお、リスト1-2はデータ準備に関する本質的なコード内容ではない(=今回のみの補助的なコードであり、コードを呼び出して実行を確認できればそれで十分である)ため、詳しいコード内容の説明は割愛する(※コード内のコメントを参考にしてほしい)。
# playground-dataライブラリのplygdataパッケージを「pg」という別名でインポート
import plygdata as pg
# 設定値を定数として定義
PROBLEM_DATA_TYPE = pg.DatasetType.RegressGaussian # 問題種別:「回帰(Regress)」、データ種別:「マルチガウシアン(Gaussian)」を選択
TRAINING_DATA_RATIO = 0.5 # データの何%を訓練【Training】用に? (残りは精度検証【Validation】用) : 50%
TEST_DATA_RATIO = 1.0 # 1.0=100%
DATA_NOISE = 0.0 # ノイズ: 0%
# 定義済みの定数を引数に指定して、データを生成する
data_list = pg.generate_data(PROBLEM_DATA_TYPE, DATA_NOISE)
test_data = pg.generate_data(PROBLEM_DATA_TYPE, DATA_NOISE)
# データを「訓練用」と「精度検証用」を指定の比率で分割し、さらにそれぞれを「データ(X)」と「教師ラベル(y)」に分ける
X_train, y_train, X_valid, y_valid = pg.split_data(data_list, training_size=TRAINING_DATA_RATIO)
X_test, y_test, _, _ = pg.split_data(test_data, training_size=TEST_DATA_RATIO)
# データ分割後の各変数の内容例として、それぞれ2件ずつ出力(※出力内容は実行ごとに異なる)
print('X_train:'); print(X_train[:2]) # [[ 5.50217882 -5.71386583] [ 2.14352675 3.23268668]]
print('y_train:'); print(y_train[:2]) # [[0. ] [0.00208684]]
print('X_valid:'); print(X_valid[:2]) # [[-3.92911409 0.87022741] [-1.79158896 5.02185125]]
print('y_valid:'); print(y_valid[:2]) # [[0.18434328] [0. ]]
print('X_test:'); print(X_test[:2]) # [[-2.56919977 -4.35912505] [ 0.82121793 1.12628696]]
print('y_test:'); print(y_test[:2]) # [[ 0. ] [-0.19976778]]
リスト1-2を見ると、今回は、座標点データセットとして、
- 訓練データ: 入力データとなる特徴量X_trainと、正解となるラベルy_train
- 精度検証データ: 特徴量X_validと、ラベルy_valid
- テストデータ: 特徴量X_testと、ラベルy_test
の3種類を用意しているのが分かる(図6)。
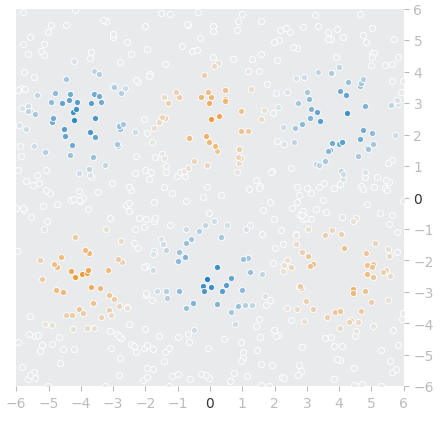
それでは、「実際にどのようなデータが生成されたか」を視覚的に確認しておこう。これを簡単に行うための関数もplayground-dataライブラリには用意されているので活用する。具体的にはリスト1-3のコードを実行してみてほしい(※このコード内容も、本質ではないので説明を割愛)。
pg.plot_points_with_playground_style(X_train, y_train)
筆者の例では図7のように描画された(※おおむね同じような描画になるが、個々の座標点の内容は実行ごとに異なる)。
バッチデータの作成について
多くの場合、データが準備できたところで、後々のミニバッチ学習用に、バッチデータ用のオブジェクトなども作成しておいた方が何かと都合がよい。
今回は、tf.kerasの基本であるcompile()&fit()メソッドを使用する。その場合、fit()メソッドがデータをミニバッチ学習用に自動分割したり、トレーニング時にエポックごとのループ処理を自動的に行ってくれたりするため、ここでバッチデータ化する必要がない。そのため、本稿では「バッチデータを作成するためのコード」は記述しない。
ちなみに、エキスパート向けである「tf.GradientTapeクラスを使ったカスタムループ」を実装する場合は、バッチデータを作成する必要がある。その方法は、「第5回 お勧めの、TensorFlow 2.0最新の書き方入門(エキスパート向け)」の2ページ目で説明している。
(2)モデルの定義
ニューラルネットワークのモデルの書き方については既に説明済みだが、再確認しておこう。今回は以下の書き方を採用する。
- tf.keras.Modelクラスをサブクラス化してモデルを定義する(初中級者以上にお勧め)
- tf.kerasの基本であるcompile()&fit()メソッドを使用する(今回はカスタムループの実装は不要なため)
ディープニューラルネットワークのモデル設計
ニューラルネットワークのモデル設計は、以下の仕様とする(※本稿の場合。もちろん、これ以外の仕様を定義してもよい。これは筆者が試行錯誤した後、より説明しやすいネットワーク構造を選択した結果である)。
- 入力の数(INPUT_FEATURES)は、X1(=X座標値)とX2(=Y座標値)で2つ
- 隠れ層のレイヤー数は、2つ
- 隠れ層にある1つ目のニューロンの数(LAYER1_NEURONS)は、4つ
- 隠れ層にある2つ目のニューロンの数(LAYER2_NEURONS)は、3つ
- 出力層にあるニューロンの数(OUTPUT_RESULTS)は、1つ
今回も隠れ層の活性化関数は、あらゆる入力値を-1.0〜1.0に変換して返すTanh関数を利用する(※次回からはより実践的な活性化関数を使っていくので楽しみにしておいてほしい)。
また、出力層の活性化関数は、線形関数/恒等関数とする。恒等関数とは、入力値をそのまま出力値として返す関数である。用語辞典「活性化関数」でも説明しているが、基本的に回帰問題では、なし(=そのまま)、もしくは恒等関数を使う。どちらでもよいが、今回は明示的にするため、恒等関数を用いた。「なし」の場合は、出力層の活性化関数自体をなくせばよい。
以上の仕様に基づくニューラルネットワークのモデル設計コードは次のようになる。このコードは、これまでの全6回の説明で何度か説明したものとほぼ同じである。コード中にはコメントも多く含めているので、説明は省略する(もし分からない部分があるようであれば、もう一度、本連載を読み返してみることをお勧めする。慣れれば簡単だ)。
import tensorflow as tf # ライブラリ「TensorFlow」のtensorflowパッケージをインポート
from tensorflow.keras import layers # レイヤー関連モジュールのインポート
from IPython.display import Image
# 定数(モデル定義時に必要となるもの)
INPUT_FEATURES = 2 # 入力(特徴)の数: 2(=X座標とY座標)
LAYER1_NEURONS = 4 # ニューロンの数: 4
LAYER2_NEURONS = 3 # ニューロンの数: 3
OUTPUT_RESULTS = 1 # 出力結果の数: 1(=結果は基本的に「-1.0」〜「1.0」の数値)
# 変数(モデル定義時に必要となるもの)
activation1 = layers.Activation('tanh' # 活性化関数(隠れ層用): tanh関数(変更可能)
, name='activation1' # 名前付け
)
activation2 = layers.Activation('tanh' # 活性化関数(隠れ層用): tanh関数(変更可能)
, name='activation2'
)
acti_out = layers.Activation('linear' # 活性化関数(出力層用): 恒等関数(固定)
, name='acti_out'
)
# tf.keras.Modelによるモデルの定義
class NeuralNetwork(tf.keras.Model):
# ### レイヤーを定義 ###
def __init__(self):
super(NeuralNetwork, self).__init__()
# 入力層は定義「不要」。実際の入力によって決まるので
# 隠れ層:1つ目のレイヤー(layer)
self.layer1 = layers.Dense( # 全結合層(線形変換)
#input_shape=(INPUT_FEATURES,), # 入力層(定義不要)
LAYER1_NEURONS, # 次のレイヤーへの出力ユニット数
name='layer1')
# 隠れ層:2つ目のレイヤー(layer)
self.layer2 = layers.Dense( # 全結合層
LAYER2_NEURONS, # 次のレイヤーへの出力ユニット数
name='layer2')
# 出力層
self.layer_out = layers.Dense( # 全結合層
OUTPUT_RESULTS, # 出力結果への出力ユニット数
name='layer_out')
# ### フォワードパスを定義 ###
def call(self, inputs, training=None): # 入力と、訓練/評価モード
# 「出力=活性化関数(第n層(入力))」の形式で記述
x1 = activation1(self.layer1(inputs)) # 活性化関数は変数として定義
x2 = activation2(self.layer2(x1)) # 同上
outputs = acti_out(self.layer_out(x2)) # そのまま出力(=「恒等関数」)
return outputs
# モデル内容の出力を行う独自メソッド
def get_functional_model(self):
x = layers.Input(shape=(INPUT_FEATURES,), name='input_features')
static_model = tf.keras.Model(inputs=[x], outputs=self.call(x))
return static_model
一点だけ注記しておくと、get_functional_modelメソッドは、次のリスト2-2でモデル内容を描画するために用意した独自の関数である(本来の処理には不要。第5回で説明済み)。
# モデル(NeuralNetworkクラス)のインスタンス化
model = NeuralNetwork()
f_model = model.get_functional_model()
f_model.summary() # モデルの内容を出力
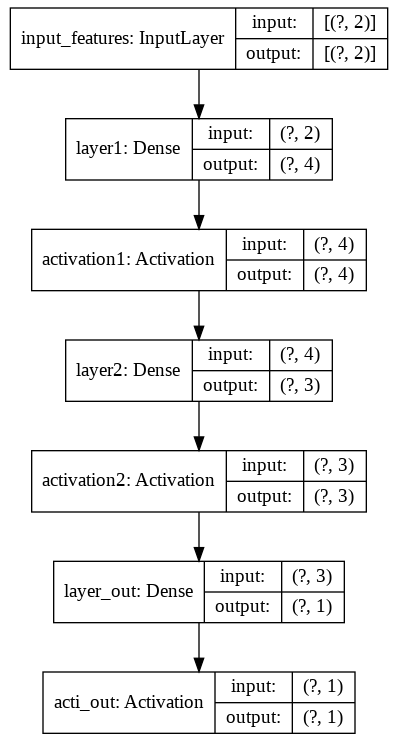
続いて、リスト2-2を実行すると、図8のように表示される。仕様通りのモデルが生成されたことが確認できる。
また、これまでの連載でも説明してきたように、モデル概要を図で描画することもできる(リスト2-3)。
# モデル概要の図を描画する
filename = 'model.png';
tf.keras.utils.plot_model(f_model, show_shapes=True, show_layer_names=True, to_file=filename)
from IPython.display import Image
Image(retina=False, filename=filename)
これを実行すると、図9のように描画される。
特に難しいところはないだろう。これまでの連載内容とほぼ同じで、これもワンパターンである。
(3)学習/最適化(オプティマイザ)
学習に関するコードも、これまでに学んで来た内容とほぼ変わらない。
# 定数(学習方法設計時に必要となるもの)
LOSS = 'mse' # 損失関数:平均二乗誤差('mean_squared_error'でもOK)
METRICS = ['mae'] # 評価関数:平均絶対誤差('mean_absolute_error'でもOK)
OPTIMIZER = tf.keras.optimizers.SGD # 最適化:確率的勾配降下法
LEARNING_RATE = 0.01 # 学習率: 0.01
# 学習方法を定義する
model.compile(optimizer=OPTIMIZER(learning_rate=LEARNING_RATE),
loss=LOSS,
metrics=METRICS) # 精度(分類では正解率。回帰では損失)
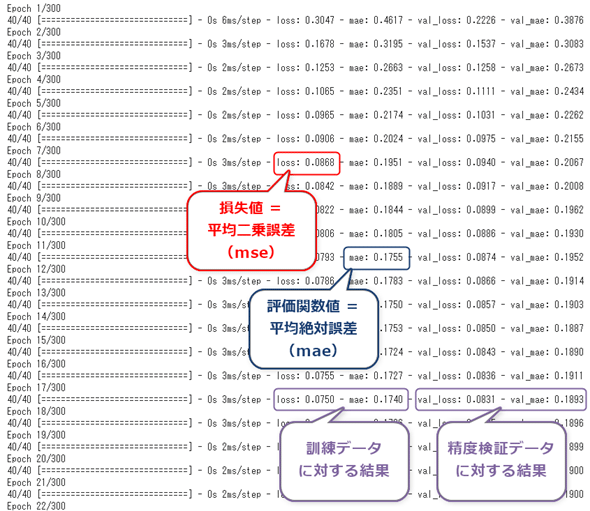
リスト3-1では、学習方法として損失関数('mse'='mean_squared_error':平均二乗誤差)や評価関数('mae'='mean_absolute_error':平均絶対誤差)、最適化(SGD:確率的勾配降下法)、学習率(0.01)を指定している(※これらの指定も、次回以降ではさまざまなものを切り替えて使っていく予定だ)。
今回のコードのポイントは、compile()メソッドの引数metrics(評価指標)である。これまでは分類問題を扱ってきたので、正解率(accuracy)という精度の評価指標/評価関数を指定していた。分類問題では、例えば犬か猫かのような判定で「正解が明確に決まる」ので正解率を指標にした方が評価しやすい。
しかし回帰問題では、正解率という評価指標は使えない。そのため(基本的に)、「出力結果の数値がどれくらい正解ラベルに近いか」という誤差(error)、もしくは正解との誤差から計算される損失(loss)が精度の評価指標/評価関数となる。今回は損失関数および評価関数として、平均二乗誤差を用いる。損失(loss)については、次のfit()メソッドで自動的に記録される仕様なので、引数metricsに明示的に評価関数として指定しなくてもよい(※もちろん['mae', 'mse']のようにして明示的に指定してもよいが、'mse'は、自動的に記録される損失'loss'と同じ値になる)。
なお、平均二乗誤差('mse')は、誤差を距離に換算する際に誤差を二乗する処理を行うため、実際の数値と単位が異なってくる。一方、平均絶対誤差('mae')はマイナスをプラスに変えているだけなので単位自体は変わっていない。よって人間にとって分かりやすいのは、平均絶対誤差の方である。そこで今回は、評価指標として平均絶対誤差('mae')も加えた。そのため、引数metricsに指定している値は['mae']となっている。
続いて、fit()メソッドを呼び出して、トレーニングを実施しよう(リスト3-2)。
# 定数(ミニバッチ学習時に必要となるもの)
BATCH_SIZE = 15 # バッチサイズ: 15(選択肢は「1」〜「30」)
EPOCHS = 300 # エポック数: 300
# 早期終了(する場合は、コメントアウトを解除)
#es = tf.keras.callbacks.EarlyStopping(monitor='val_loss', patience=5)
# 学習する
hist = model.fit(x=X_train, # 訓練用データ
y=y_train, # 訓練用ラベル
validation_data=(X_valid, y_valid), # 精度検証用
batch_size=BATCH_SIZE, # バッチサイズ
epochs=EPOCHS, # エポック数
verbose=1, # 実行状況表示
callbacks=[ # コールバック
#es # 早期終了(する場合はコメントアウトを解除)
])
基本的なDNNでは通常、ミニバッチ学習を行う(このことは、連載第3回の2ページ目で説明済み)。今回はそのバッチサイズを15、トレーニング単位であるエポック数は300とした。
今回は早期終了(Early Stopping)を行わないが、試しやすいように、サンプルコードをコメントアウトした状態で、リスト3-2に含めておいた。早期終了の実装方法については、第3回の3ページ目で説明済みだ。
以上のリスト3-2までのコードを実行すると、モデルのトレーニングが実施される(図10)。
(4)評価/精度検証
あとは、出来上がった学習済みモデルの精度検証(validation)を行い、「このまま学習を完了とするか」「ハイパーパラメーター(=リスト2-1のモデル定義やリスト3-1の学習方法の定義、リスト3-2のトレーニングの各コード内に記載した各定数の値)を変えて試行錯誤するか」を決める。この精度検証による評価の手順も、第3回の3ページ目で説明したものと変わらない。
今回も、学習結果(損失の履歴)をグラフに描画してみよう。そのコードも、リスト4-1の通り、ワンパターンだ(※グラフが2つになっているが、基本は同じようなコード)。
import matplotlib.pyplot as plt
# 学習結果(損失=平均二乗誤差)のグラフを描画
plt.figure()
train_loss = hist.history['loss']
valid_loss = hist.history['val_loss']
epochs = len(train_loss)
plt.plot(range(epochs), train_loss, marker='.', label='loss (training data)')
plt.plot(range(epochs), valid_loss, marker='.', label='loss (validation data)')
plt.legend(loc='best')
plt.grid()
plt.xlabel('epoch')
plt.ylabel('loss (mean squared error)')
# 評価関数(平均絶対誤差)のグラフを描画
plt.figure()
train_mae = hist.history['mae']
valid_mae = hist.history['val_mae']
epochs = len(train_mae)
plt.plot(range(epochs), train_mae, marker='.', label='mae (training data)')
plt.plot(range(epochs), valid_mae, marker='.', label='mae (validation data)')
plt.legend(loc='best')
plt.grid()
plt.xlabel('epoch')
plt.ylabel('mean absolute error')
plt.show()
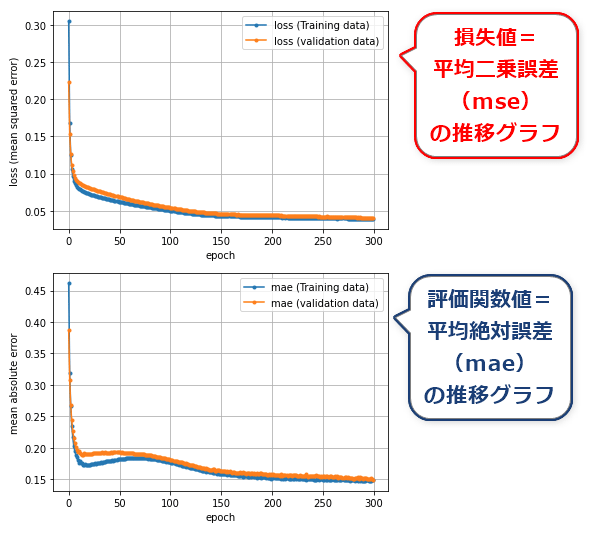
このコードを実行すると、筆者の場合は図11のようなグラフが描画された。
筆者の実行例では、訓練データでも精度検証データでも同じように損失が下がっており、過学習もなく順調に学習が進んだようである(※ちなみに次回では過学習が起こった場合を体験してみる)。
評価関数('mae':平均絶対誤差)の結果値は、約0.15にまで下がっている。つまり、今回の学習済みモデルで推論すると、その結果値は平均して±0.15ぐらいの誤差が生まれる、ということである。これが許容できるようであれば本番運用が可能だろう。これぐらいの誤差であれば、「大体はオレンジ色(-1.0)〜白色(0.0)〜青色(1.0)」という予測がほぼ正確にできている状態と判断してもよいだろう。そこで、今回はこの学習済みモデルを運用に回すことにする。
(5)テスト/未知データによる評価
ただし実運用に入る前に念のため、未知データによるテスト、つまり汎化性能の評価を行って、「学習済みモデルが実運用できるか状態か」を最終確認しておこう(リスト5-1)。
#BATCH_SIZE = 15 # バッチサイズ(リスト3-2で定義済み)
# 未知のテストデータで学習済みモデルの汎化性能を評価
score = model.evaluate(X_test, y_test, batch_size=BATCH_SIZE)
print('test mae:', score[1])
# 出力例:
# 80/80 [===……===] - 0s 931us/step - loss: 0.0375 - mae: 0.1453
# test mae: 0.1452532261610031
リスト5-1を実行した結果、評価関数('mae':平均絶対誤差)の結果値として0.1452532261610031が出力された。この数値は、前述の評価/精度検証とほぼ変わらないので、未知のテストデータにおいても十分な性能を発揮していると判断できる。よって、本番での実運用が可能だ。
学習済みモデルによる推論結果のヒートマップ
さて、今回はおまけとして、学習済みモデルによる推論の結果を一望できるヒートマップ(詳細後述)も簡単に作ってみることにしよう。
ここで言う「ヒートマップ」とは、推論結果が背景画像のようにグラデーション描画される図で、オレンジ色(-1.0)〜白色(0.0)〜青色(1.0)で表現される。色は、各座標点における学習済みモデルの推論結果を意味する。例えばPlaygroundでトレーニングを実行すると、図12のようなヒートマップが描画できる。今回はこれと全く同じ形式のヒートマップを作成することにしよう。
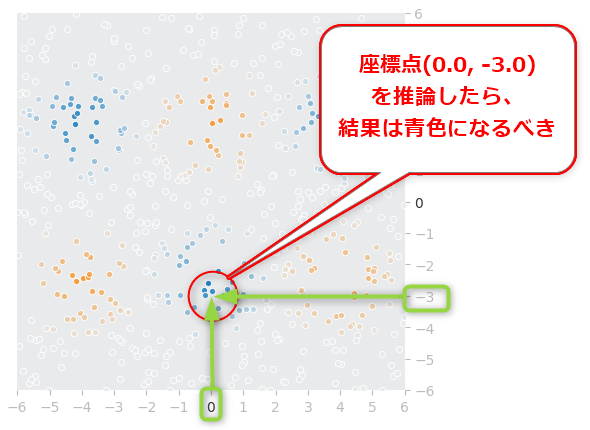
再確認のため、入力データとして使った座標点データセットを、もう一度、図に描画してみよう(リスト5-2、図13)。
pg.plot_points_with_playground_style(X_train, y_train)
図13のグラフ内容を把握したうえで、このグラフで青い部分の座標である座標点(0.0, -3.0)を学習済みモデルに入力して、試しに結果を予測、つまり「推論」してみよう。具体的にはリスト5-3のようなコードを書けばよい。
# 推論(予測)する
model.predict([[0.0, -3.0]])
# array([[0.2751151]], dtype=float32) ……などと出力される
リスト5-3では、筆者の場合、「0.2751151」(=やや青色)が出力された。前掲の図13に示されているように、入力した座標点付近は青色(=1.0)に近いので、正解に近い結果となっているのが分かる。
推論結果のヒートマップを作りたい場合は、このような推論を、XY座標系グラフの全面で行えばよい(※以降、Pythonコードの説明としては少し難易度が高いので、理解できなくても、そのまま読み飛ばしてもらって構わない)。例えば-6.0〜6.0の範囲を100分割して、X座標値/Y座標値ともに0.12刻みの100×100=1万個の画素を作る。そのようにして作成した1万個の画素に対応する座標点データセットをまとめて推論すればよい。あとは各座標点の背景色として、
- 予測値が-1.0の箇所: オレンジ色
- 予測値が0.0の箇所: 白色
- 予測値が1.0の箇所: 青色
という3つの基点を作る。そして、オレンジ色(-1.0以下)〜白色(0.0)、さらに白色(0.0)〜青色(1.0以上)でグラデーションを作る。出来上がったグラデーション配色で背景を描画すれば、ヒートマップの完成である。
ただし、このままだと背景の画素ごとにカクカクした描画となる。滑らかな描画にするには、画素間を補間(interpolation)すればよい。グラフ描画ライブラリ「Matplotlib」のimshow()メソッドには引数interpolationが用意されており、例えば文字列で'bicubic'を指定すれば「バイキュービック補間(双三次補間)」が簡単に実現できる(実装コード例はこちら)。
以上の内容をPythonコードで書けば、前掲の図12に示したようなヒートマップができる……が、そのようなコードを実際に書くのは面倒くさいだろう。ライブラリ「playground-data」には、そのような学習結果のヒートマップ(分類問題における「決定境界」にもなる)を描画するためのdraw_decision_boundary関数が用意されているので、これを利用してヒートマップの描画作業は一瞬で終わらせよう。具体的にはリスト5-4のようなコードを記述すればよい(※これも今回限りのコードであり、DNNにおいて本質的なコードではないので、詳しい説明は割愛する)。
# ヒートマップ/決定境界のグラフを描画する
fig = pg.get_playground_figure()
ax = pg.get_playground_axes(fig)
pg.draw_decision_boundary(fig, ax, trained_model=model)
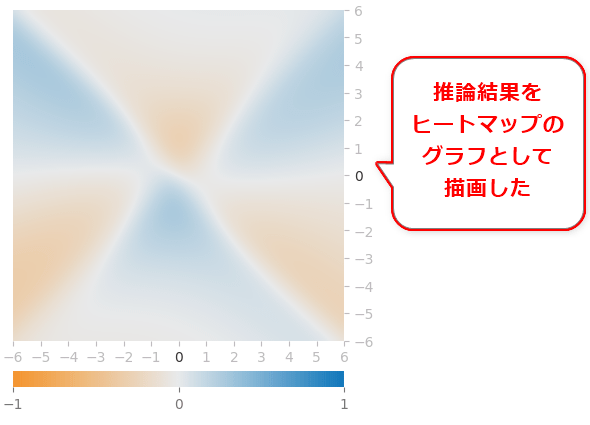
このコードを実行すると、図14のような学習結果のグラフを描画できる。
次回について
以上、今回は基本的なDNNで「回帰問題」を解決した。これまでの連載記事とほぼ同じような流れとコードで実装できることが体感できただろうか。このような、ディープラーニングの基本部分はワンパターンで、あまり難しくない(難しいと感じる場合は、まだ慣れていないだけだと思う)。
今後の連載では、このワンパターンを繰り返しながら応用力を付けていく。次回は、Fashion-MNISTという画像データセットを入力とし、今回と同じように基本的なDNNで「分類問題」を解いてみる。DNNで使う活性化関数など少しずつレベルを上げていくが、これまでの知識だけで画像認識が行えることを示す。
Copyright© Digital Advantage Corp. All Rights Reserved.