 |
連載コラム
鈴木純一の「世界は狭い？」
鈴木純一
カリフォルニア大学 アーバイン校
2001/12/1
| 初めて出会った人との間に共通の友人がいると「世界は狭いですねぇ」などという。こうした狭い世界、あるいは小さな世界の現象を解析し、工学的に応用しようとする動きがあちこちで見られるようになってきた。例えば、ネットワークトポロジの決定シミュレーション、エージェントの協調設計、PtoP（Peer-to-Peer）アーキテクチャにおける分散検索（分散インデックスによる検索）、グリッドコンピューティング、コミュニティコンピューティングなどにおける応用である。本コラムでは、この「狭い世界」の特徴を概観し、ソフトウェアシステムへのさまざまな応用を考える。 |
第1回 狭い世界のネットワークとは
 |
「狭い世界」とは |
狭い世界という現象は、心理学者のスタンリー・ミルグラムが1960年代後半に提唱した「6次の隔たり（Six Degrees of Separations）」という概念から発展している。この概念は、社会において人間同士がどのように結ばれているのかを明らかにする概念で、6人の共通の知人の連鎖を介せば、世界中のすべての人間と間接的な知人関係を結べる、という考え方である。例えば、自分に10人の知人がいるとして、その知人にも10人の知人がいるとする。これを6回繰り返すと、自分には1000万人の間接的な知人がいることになる。ここで知人関係をそれぞれ20人だとすると、間接的に20の7乗つまり12億8000万人の知人が存在することになる。こうしたことから、昔から、少ない知り合い関係の連鎖で（つまり少ないホップで）世界中の人間すべてと間接的な友人関係を結べるのではないかといわれてきた。これを実際に実験で試したのがミルグラムである。
ミルグラムは、チェーンレター（「不幸の手紙」のようなもの）による実験を行った。ネブラスカ州オハマに住む160人の住人をランダムに選択し、それぞれの知人へ手紙を転送しながら、ボストン在住のある人へその手紙を届けるよう依頼したのである。この結果、ほとんどの手紙が5段階か6段階の知人を経ることでゴールのあて先に届いていることが分かった。日本の社会学者も同様の実験を行い、九州から始めて「北海道の知り合いを紹介してください。もしいなければ、北海道に知り合いがいそうな人を紹介してください」と尋ねて何人目で北海道にたどり着くかを計測した。結果は平均で7人だった。
同じような実験として、映画好きのコミュニティーにおける「ベーコン数」という概念が知られている。これは、ある俳優／女優が直接ケビン・ベーコンと共演したことがあればベーコン数1、自分と共演した人がケビン・ベーコンと共演していればベーコン数2というように、ケビン・ベーコンとの共演関係の近さを測るためのものである。バージニア大学の研究グループがこの数値を計測しており[1]、その結果、
ベーコン数1の人：1384人
ベーコン数2の人：9万3760人
ベーコン数3の人：19万6582人
…
となり、ハリウッド俳優／女優のベーコン数平均は2.86になっている（11万本の映画から22万5226人の俳優／女優を対象に計測）。同様に、ショーン・コネリーと共演したことのある人を「コネリー数」として計測したところ、コネリー数の平均は2.64となっている。つまり、ハリウッドに生息する俳優／女優を任意に2人選ぶと、その両者の間の知り合い関係は6段階以内で収まるということである（ケビン・ベーコンを介せば2.86*2回、ショーン・コネリーを介せば2.64*2回）。別の見方をすれば、ベーコンやコネリーのように顔の広い人が1人か2人いれば、それだけで関係のない2人を結び付けることができてしまう、ということを意味している。さらには、モニカ・ルインスキー数というのを数えている人たちもいて[2]、ケビン・ベーコンとは6ホップ、ジム・キャリーとも6ホップ、そしてキューバのカストロ議長とは何と4ホップであることが判明した。
こうした「ねずみ講」的なネットワーク、あるいは草の根ネットワークの現象は、ほかの分野でも知られている。例えば、『ティッピング・ポイント』という本[3]では、物事が伝染病的に世の中に広がる現象を説明しており、そこには狭い世界のような現象が起きていることが述べられている。「ティッピング・ポイント」とは、あるアイデアや流行、社会的行動が敷居を越えて一気に流れ出し、野火のように広がる劇的瞬間を指している。また『ヒット・エコノミー戦略』という本[4]では、ファッションやファッド（一時的流行）が発生する現象についても述べている。予想をはるかに超えて『ハリーポッターの賢者の石』が一躍ベストセラーになったり、広告宣伝にまったく力の入っていなかった映画『フルモンティ』がいきなりブレイクしたり……などなど、「急激で大きな変化」を引き起こす「小さな原因」を突き止めようとすると、そこには常に狭い世界に類似した現象が起きていることが分かる。
さらに、伝染病のまん延現象は狭い世界の現象と同じであることが世界中の関係者によって報告されている。例えばエイズをまん延させるには、エイズ感染者と非感染者がランダムに性交渉をするよりも、非感染者と次々に性交渉するエイズ感染者が少数いるだけで十分であることが知られている。
こうした狭い世界の現象で特徴的なのは、個々人はそれほど広範囲で多岐にわたる交友関係を持っているわけではないということである。個々人はごく限られた範囲内でローカルな交友関係を持っているだけなのに、地球の裏側で生活している見ず知らずの人と間接的なリンクを少ないホップ数で張ることができるのである。別のいい方をすれば、ローカルには密接していて、グローバルにはまばらなネットワークができているといえる。なお、ミルグラムが提唱した「Six Degrees of Separation」は舞台劇から映画化もされており、『私に近い6人の他人』という邦題が付けられている。筆者はまだこの映画を見るチャンスに恵まれていないが、どなたかご覧になられた方がおられたらぜひ感想などを聞かせてください。
|
ネットワーク（グラフ）から見た「狭い世界」 |
それでは、狭い世界の特性を理解するために、ネットワーク（グラフ）構造の観点から狭い世界を位置付けてみたい。ケビン・ベーコンの例でいえば、俳優／女優がノード、共演関係がノード間のリンクに相当する。
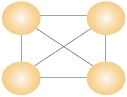
まず始めに、個々のノードがほかのノードすべてを知っている、という完全グラフを考える（図1）。
 |
|
図1
|
このネットワークの上でノードがやりとりするときの利点は、
- 個々のノードがネットワーク上の情報（ノード）をすべて知っている
- どのノードもほかのノードと1ホップで通信可能
- あるノードに障害が生じてもほかのノードとは通信可能。つまりボトルネックが存在しない。柔軟性は高い
ことであろう。しかし一方で、
- ノードの数が増えると、n*(n-1)/2個のリンクを設定、維持するコストを無視できなくなる（nはネットワーク上のノード数）。拡張性は低い
- 個々のノードが自分以外のすべてのノード（n-1個のノード）を知り得ることができるとは限らない
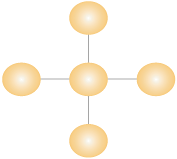
という重大な欠点を持っている。この欠点を回避するネットワーク構造として図2のようなスター型のネットワークがある。
 |
|
図2
|
中央にハブとなるノードがあり、ほかのノードはすべてこのハブと接続するネットワークである。コンピュータネットワークの世界でいえばハブやスイッチ、ルータを介した接続、分散システムの文脈でいえばディレクトリサービスを介した接続などが、このネットワーク構造の応用例である。また、航空会社がフライト路線を設計する際にもハブ空港を決めて路線を設定している。こうしたスター型ネットワークの利点は、
- 任意のノード間には2つの隔たりしかなく高速
- ネットワーク構造が直感的に理解しやすい
- ノード間に張るリンクの数は少なくて済む（リンク維持のコストは低い）
である。一方、欠点としては、
- ノード間でやりとりするには必ずハブを経由する必要があり、ハブに障害が生じるとすべての通信が遮断されるため、ネットワーク全体の耐障害性は低い
- 1.と同様の理由により、ノード数が増加するとハブが通信上のボトルネックになりやすく、拡張性が低い
が挙げられる。上記2つのネットワーク構造が抱える欠点、つまり拡張性の低さを改善するネットワーク構造としては、スター型＋完全グラフの構造も考え得る（図3）。
 |
|
図3
|
これは、スター型のハブを複数個用意して、ハブ同士を完全グラフとして接続するものである。図3において、ハブAに障害が生じて利用不可能となっても、ノード2、3、4は互いに通信可能である（ノード1は通信不可）。分散システムにおいてディレクトリサービスを複数個連結するフェデレーション構成などはこの一例である。
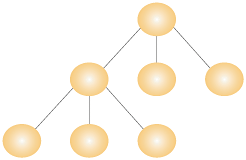
ツリー型のネットワーク構造も拡張性を備えたネットワークである（図4）。
 |
|
図4
|
ツリー構造は、大量の情報を管理するときに利用する常とう手段といえるだろう。例えば、ファイルシステムのディレクトリ構造、ディレクトリサービスの内部構造などに利用されている。このネットワークの利点は、
- 構造を直感的に理解できる
- ノード数の増加に対して拡張性がある。ノードのトレースが容易
である。一方、欠点は以下のとおりだ。
- 親ノードに障害が生じると、その子どもは通信できなくなる
- ツリーを上下しながら通信をする必要があり、ノード間のホップ数は大きくなる傾向がある
- ノードの移動や、リンクの張り替えなどに対する柔軟性が低い
こうした欠点のうち(1)と(2)を克服する拡張モデルとして、図5のようなネットワーク付きツリーの構造が考えられる。
 |
|
図5
|
これは、ツリー内の兄弟ノード（同一の親ノードに接続しているノード）を完全グラフで接続したものである。これにより、
- ツリーを上下せずにノード間通信を実現できる場合がある。例えば図5で、ノード3とノード6の通信は3-2-6のパスで実現できるが、純粋なツリーの場合には3-1-2-6となる
- 親ノードを介さずに、兄弟ノード間で直接通信できる
という利点が生まれる。
これまで見てきたように、ネットワーク全体が完全グラフであることは好ましくないが、ネットワーク付きツリーやスター型＋完全グラフのように、ネットワーク内の一部分が完全グラフになっているメリットは大きいことが分かる。
 |
|
図6
|
さてここで、完全グラフとの比較のために、ランダムグラフ（図6）の特徴を見てみる。ノードとノードのリンクをランダムに結んだグラフである。利点としては、
- あるノードが障害に陥ってもネットワーク全体が停止することはない
- ノード数の増加に対して拡張性がある
- 比較的小さなホップ数でノード間を結べる可能性がある。ただし、ランダムなリンク付けが行われるのでホップ数が大きくなることもあるし、任意の2点間を結べない場合もあり得る
が挙げられる。ただし、欠点としては、すべてが確率的に決定づけられるネットワークというのは実世界にはほとんど存在しない。一見ランダムに見える人間の「知り合い関係」でさえ、家族、所属組織、人種、居住地域などに多かれ少なかれ依存している。
それでは、先のセクションで紹介した狭い世界はどんな構造を持ったネットワークなのだろうか。先に述べたように、狭い世界はローカルには密接していて、グローバルにはまばらなネットワークである。こうしたネットワークは、完全グラフでもランダムグラフでもなく、両者の間に存在する。
本連載コラム第1回は、狭い世界の特徴を概観した。次回は、狭い世界のネットワーク構造を明らかにする先駆的な研究結果と最近の動向をまとめたい。
参考
[1] http://www.cs.virginia.edu/oracle/center.html
[2] http://wwwcsif.cs.ucdavis.edu/~chirapun/lewinsky.html
[3] 『ティッピング・ポイント』（マルコム・グラッドウィル著／飛鳥新社）
[4] 『ヒット・エコノミー戦略』（ウィンスロー・ファラル著／レゾナンス）
次回は12月下旬の公開予定です。
| プロフィール | ||
鈴木純一（すずき じゅんいち） カリフォルニア大学アーバイン校にて、次世代分散システムの研究開発に従事。また（株）オージス総研ソフトウェア工学センターのアドバイザリーボードメンバー、（株）シナジー研究所の技術顧問を務める。カリフォルニア大学以前は、オブジェクト技術の標準化団体であるオブジェクトマネジメントグループの日本法人OMGジャパン、(株)創研プランニングにて、企業および政府機関に対してオブジェクト技術／分散オブジェクト技術のコンサルティング、導入支援、教育を手掛ける。工学博士。
（筆者の技術情報公開ページでは、筆者の日頃の研究内容や講演資料などが公開されています。また、更新の度にメールマガジンが発行されています。メールマガジンの登録はこちら）
|
 |
ご意見、ご感想は掲示板へどうぞ |
- 実運用の障害対応時間比較に見る、ログ管理基盤の効果 （2017/5/9）
ログ基盤の構築方法や利用方法、実際の案件で使ったときの事例などを紹介する連載。今回は、実案件を事例とし、ログ管理基盤の有用性を、障害対応時間比較も交えて紹介 - Chatwork、LINE、Netflixが進めるリアクティブシステムとは何か （2017/4/27）
「リアクティブ」に関連する幾つかの用語について解説し、リアクティブシステムを実現するためのライブラリを紹介します - Fluentd＋Elasticsearch＋Kibanaで作るログ基盤の概要と構築方法 （2017/4/6）
ログ基盤を実現するFluentd＋Elasticsearch＋Kibanaについて、構築方法や利用方法、実際の案件で使ったときの事例などを紹介する連載。初回は、ログ基盤の構築、利用方法について - プログラミングとビルド、Androidアプリ開発、Javaの基礎知識 （2017/4/3）
初心者が、Java言語を使ったAndroidのスマホアプリ開発を通じてプログラミングとは何かを学ぶ連載。初回は、プログラミングとビルド、Androidアプリ開発、Javaに関する基礎知識を解説する。
 |
|
|
|
|
