word2vecリターンズ！ 品詞分類による精度改善：ディープラーニング習得、次の一歩（2/2 ページ）

[石垣哲郎，著]

ニューラルネットワーク構築

　今回は入出力データが単語と品詞の2種類あるので、KerasのFunctional APIを用いてニューラルネットワークを構築する。

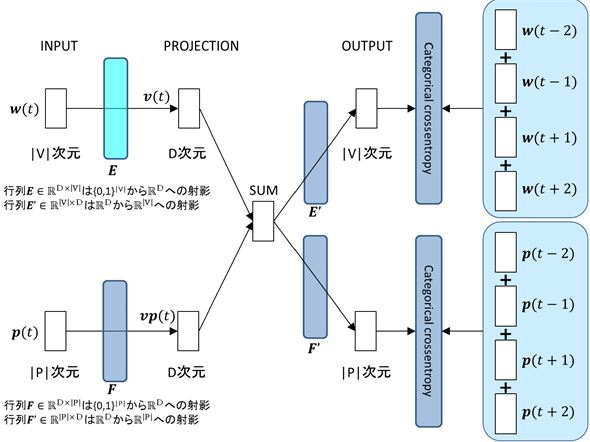
　基本的な考え方は、それぞれのデータを同次元のベクトル空間にEmbeddingし、その結果を足し合わせたうえで、それぞれのデータごとにDense-Softmax演算を行って学習を進める。こうすることによって、品詞データの学習結果が単語のEmbedding重み行列（＝求めるベクトル表現）にも反映されることを意図している。図3にそのイメージを示す。

図3　ニューラルネットワークのイメージ

　図においてVは語彙集合、|V|はその要素数すなわち語彙数、Dは埋め込みベクトルの次元である。また、wは各単語のone-hotベクトル表現、vはその埋め込みベクトル表現、Eはwからvへの変換行列、E'はvを|V|次元空間に射影する行列である。これらの意味は、前掲の図1と同じである。

　また、Pは品詞集合、|P|はその要素数すなわち品詞分類数である。また、pは各単語の品詞分類のone-hotベクトル表現、vpはその埋め込みベクトル表現、Fはpからvpへの変換行列、F'はvpを|P|次元空間に射影する行列である。

　図に現れる4つの行列のうち、Eが求めるベクトル表現の行列である。

　KerasのFunctional APIというのは文字どおり、ニューラルネットワークの各レイヤー処理を関数インターフェースで実現するもので、入力が1つ前のレイヤーの処理結果、出力がそのレイヤーの処理結果である。この仕組みにより、ニューラルネットワークを分岐させたり合流させたり、あるいは複数の入出力を持たせたりすることが、容易にできる。直感性ではSequentialモデルに一歩譲るものの、慣れてくればなかなか便利である。

　今回も学習の発散を防ぐため、EarlyStopping（＝学習を適切なタイミングで早期に打ち切る機能）を使用する。今回は正解率を計算する仕組みを用意したので、普通に損失関数lossを監視対象とする。

class Prediction :
  def __init__(self, input_dim, output_dim, part_dim):
    self.input_dim = input_dim
    self.output_dim = output_dim
    self.part_dim = part_dim

  def create_model(self):
    word_input = Input(shape=(1,), dtype='int32', name='word_input')
    x_w = Embedding(output_dim=self.output_dim, input_dim=self.input_dim, input_length=1,
                    embeddings_initializer=uniform(seed=20170719))(word_input)
    part_input = Input(shape=(1,), dtype='int32', name='part_input')
    x_p = Embedding(output_dim=self.output_dim, input_dim=self.part_dim, input_length=1,
                    embeddings_initializer=uniform(seed=20170719))(part_input)
    x = keras.layers.add([x_w , x_p])
    x = Flatten()(x)
    word_output = Dense(self.input_dim, use_bias=False,activation='softmax', name='word_output',
                        kernel_initializer=glorot_uniform(seed=20170719))(x)
    part_output = Dense(self.part_dim, use_bias=False,activation='softmax', name='part_output',
                        kernel_initializer=glorot_uniform(seed=20170719))(x)
    model = Model(inputs=[word_input, part_input], outputs=[word_output, part_output])
    model.compile(optimizer='RMSprop',
        loss = {'word_output': 'categorical_crossentropy', 'part_output': 'categorical_crossentropy'},
        loss_weights = {'word_output': 1., 'part_output': 0.2})

    return model

  # 学習
  def train(self, x_train, t_train,x_p_train,t_p_train,batch_size,epochs, emb_param) :
    early_stopping = EarlyStopping(monitor='loss', patience=1, verbose=1)
    model = self.create_model()
    #model.load_weights(emb_param)               # 埋め込みパラメーターセット
    model.fit({'word_input': x_train, 'part_input': x_p_train},
              {'word_output': t_train, 'part_output': t_p_train},
                batch_size=batch_size, epochs=epochs,verbose=1,
                shuffle=True, callbacks=[early_stopping], validation_split=0.0)

    return model

リスト7　ニューラルネットワーク本体

　単語データの入力をword_input、品詞データの入力をpart_inputとして定義し、それらのEmbedding結果をそれぞれx_w、x_pとする。

　これらを足し合わせたxに対し、それぞれ別次元のDenseを施行して出力word_output、part_outputを得る、という流れである。

　compileメソッドのパラメーターloss_weightsは、今回のように複数の入出力がある場合に、それらの損失関数にどのように重みを付けて、全体の損失関数を計算するかを指定するものである。

メイン処理

　上記で定義したニューラルネットを動かして、学習を進める。

vec_dim = 400 
epochs = 1
batch_size = 200
input_dim = len(words)
output_dim = vec_dim
part_dim = len(parts)

prediction = Prediction(input_dim, output_dim, part_dim)

emb_param = 'param_skip_gram_' + str(maxlen) + '_' + str(vec_dim) + '.hdf5'    # パラメーターファイル名
print(emb_param)

row=t_train.shape[0]

t_one_hot = np.zeros((row, input_dim), dtype='int8')     # ラベルデータをn-hot化
for i in range(0, row) :
  for j in range(0, maxlen*2):
    t_one_hot[i, t_train[i,j]] += 1
  if i % 50000 == 0 :
    print(i)
print(t_one_hot.shape)

t_p_one_hot = np.zeros((row, part_dim), dtype='int8')    # ラベルデータをn-hot化
for i in range(0, row) :
  for j in range(0, maxlen*2):
    t_p_one_hot[i, t_p_train[i,j]] += 1 
  if i % 50000 == 0 :
    print(i)
print(t_p_one_hot.shape)

model = prediction.train(x_train, t_one_hot, x_p_train, t_p_one_hot, batch_size, epochs, emb_param)

model.save_weights(emb_param)                    # 学習済みパラメーターを保存

リスト8　メイン処理

　ラベルデータを「n-hot」化する処理は、Pythonなのにループを二重に回しているため、非常に重い。これの改善については、読者諸氏に任せることとしたい（爆）。

正解率の算出

　学習終了後に、あらためて正解率を算出する。考え方は先に記述したとおりである。

x_eval = x_train[:40000,:]
x_p_eval = x_p_train[:40000,:]
t_eval = t_one_hot[:40000,:]

y_pred = model.predict([x_eval, x_p_eval], batch_size=batch_size, verbose=1)   # 評価結果

n_true = 0
n_pred = 0
for i in range(0, x_eval.shape[0]) :
  label = set(t_one_hot[i,:].nonzero()[0])
  n_true += len(label)
  argmax_pred = y_pred[0][i,:].argsort()[::-1][0:len(label)]

  hit = set(label) & set(argmax_pred)

  n_pred += len(hit)
  del label,argmax_pred
  del hit

print()
print('正解率 =', n_pred * 1.0 / n_true )

リスト9　正解率算出

　コーパス全量を使って正解率を計算するのは時間がかかるので、ここでは使用データ量を40000個に絞っている。

　行単位に正解率を算出し、それらを足しあわせて最終的な正解率を求める。各行において、labelは「n-hot」化したラベルデータの中で0でないものの集合、argmax_predは予測結果のうち、大きい方からlen(label)数を抽出した集合である。

　この2つの集合の共通要素数が正解数であり、これを使って正解率を算出している。

評価

　まず、学習した重み行列の構成を確認する。get_weights()やload_weights()、save_weights()で扱っているパラメーターファイルは、重み行列のリストになっているので、それらのshapeを表示してみる。

param_list = model.get_weights()
print(len(param_list))
for i in range(0, len(param_list)):
  print(param_list[i].shape)

リスト10　重みパラメーターファイルの構成確認

　今回の場合、リスト10を実行すると、重み行列が4つあることが分かるが、その0番目の行列が求める埋め込み行列である。この行列のi行目の行ベクトルがインデックスiの単語のベクトル表現になっている。

　演算の結果がどの単語に近いのかは、「コサイン類似度」で評価する。コサイン類似度とはひと言でいうと、2つのベクトルが見込む角度の余弦である。当然、値の範囲は-1〜1で、1に近いほど（要は大きいほど）類似度が高いと評価する。

　苗字当ては以下のコードで実施する。コサイン類似度の計算ロジックは、前回記事と同じである。

param = param_list[0]

word_m0 = '明智'
word_m1 = '小五郎'

word0 = '清太郎'
word1 = '清一郎'
word2 = '勇'
word3 = '武'
word4 = '廣介'
word5 = '源三郎'
word6 = '三郎'
word7 = '早苗'
word8 = '潤一'
word9 = '葉子'
word10 = '庄兵衛'

vec0 = param[word_indices[word_m0],:]
vec1 = param[word_indices[word_m1],:]
vec2 = param[word_indices[word2],:]

for i in range(0,11) :
  vec2 = param[word_indices[eval('word'+str(i))],:]
  vec = vec0 - vec1 + vec2
  vec_norm = math.sqrt(np.dot(vec, vec))

  w_list = [word_indices[word_m0], word_indices[word_m1], word_indices[eval('word'+str(i))]]
  dist = -1.0
  m = 0
  for i in range(0, len(words)) :
    if i not in w_list :
      dist0 = np.dot(vec, param[i,:])
      dist0 = dist0 / vec_norm / math.sqrt(np.dot(param[i,:], param[i,:]))
      if dist < dist0 :
        dist = dist0
        m = i
  print('コサイン類似度=', dist, ' ', m, ' ', indices_word[m])

リスト11　苗字当て評価

　結果は以下のとおりである。正解率はほとんど変らないが、精度はさらに向上していることが分かる。

品詞分類	無し	有り
正解率	0.393821	0.394787
黒田清太郎	×	○
蕗屋清一郎	×	×
斎藤勇	×	○
松村武	×	○
人見廣介	○	○
菰田源三郎	○	○
郷田三郎	○	○
岩瀬早苗	×	×
雨宮潤一	×	○
桜山葉子	×	○
岩瀬庄兵衛	○	○
表3　苗字当ての結果

　同じ要領で、肩書が当てられるかどうかも試してみた。「明智」−「探偵」の対に対し、以下の肩書から苗字が当てられるかどうかを評価した。

苗字	肩書	登場作品
宗像	博士	悪魔の紋章
笠森	判事	心理試験
小林	刑事	Ｄ坂の殺人事件
緑川	夫人	黒蜥蜴
中村	警部	悪魔の紋章
表4　登場人物の肩書一覧

　コードは以下のとおり。苗字当てのときとほぼ同じである。

param = param_list[0]

word_m0 = '明智'
word_m1 = '探偵'

word0 = '博士'
word1 = '判事'
word2 = '刑事'
word3 = '夫人'
word4 = '警部'

vec0 = param[word_indices[word_m0],:]
vec1 = param[word_indices[word_m1],:]
vec2 = param[word_indices[word2],:]

for i in range(0,5) :
  vec2 = param[word_indices[eval('word'+str(i))],:]
  vec = vec0 - vec1 + vec2
  vec_norm = math.sqrt(np.dot(vec,vec))

  w_list = [word_indices[word_m0], word_indices[word_m1], word_indices[eval('word'+str(i))]]
  dist = -1.0
  m = 0
  for i in range(0,len(words)) :
    if i not in w_list :
      dist0 = np.dot(vec,param[i,:])
      dist0 = dist0 / vec_norm / math.sqrt(np.dot(param[i,:], param[i,:]))
      if dist < dist0 :
        dist = dist0
        m = i
  print('コサイン類似度=', dist,' ', m, ' ', indices_word[m])

リスト11　苗字当て評価

　結果は以下のとおり。なかなかの正答率である。

苗字	肩書	結果
宗像	博士	○
笠森	判事	○
小林	刑事	×
緑川	夫人	○
中村	警部	○
表5　登場人物の肩書一覧

前後の単語数を増加させた時の結果

　原論文では、skip-gramの評価に使う、前後の単語数を増加させると、精度が改善するとあった。そこで、これを試してみる。リスト6のmaxlenで単語数を指定しているので、これに20、30、50を設定して、結果を比べた。以下にそれを示す。

	評価尺度	人物名／肩書	maxlen=10	maxlen=20	maxlen=30	maxlen=50
	正解率	−	0.394787	0.403926	0.403629	0.399828
	苗字当て	黒田清太郎	○	○	○	○
		蕗屋清一郎	×	○	×	○
		斎藤勇	○	○	○	×
		松村武	○	○	○	○
		人見廣介	○	○	○	×
		菰田源三郎	○	○	○	○
		郷田三郎	○	×	×	×
		岩瀬早苗	×	×	×	×
		雨宮潤一	○	×	○	○
		桜山葉子	○	○	○	○
		岩瀬庄兵衛	○	×	○	○
		平均cos類似度	0.365922	0.386849	0.415611	0.410962
	肩書当て	宗像博士	○	○	○	○
		笠森判事	○	○	○	○
		小林刑事	×	×	○	○
		緑川夫人	○	○	○	○
		中村警部	○	○	○	○
		平均cos類似度	0.465800	0.533170	0.505446	0.544478
表3　苗字当ての結果

　さらなる劇的な効果を期待していたのだが、正解率や予測精度は横ばいである。しかし、予測的中時の平均コサイン類似度は、改善傾向にある。

終わりに

　本稿では、word2vecの学習データに品詞分類を追加することによって、予測精度が改善するかどうかを検証してみたが、これは確かに効果があった。他の自然言語処理でも効果が期待できるので、そのような機会があった際には、ぜひ試していただきたい。

「ディープラーニング習得、次の一歩」