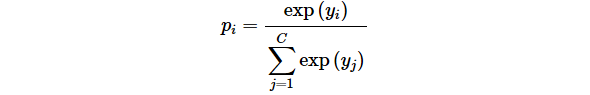第4回 CNN(Convolutional Neural Network)を理解しよう(TensorFlow編):TensorFlow入門
画像認識でよく使われるディープラーニングの代表的手法「CNN」を解説。「畳み込み」「プーリング」「活性化関数」「CNNのネットワーク構成」「ソフトマックス関数」といった基礎と、注意点を押さえよう。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
ご注意:本記事は、@IT/Deep Insider編集部(デジタルアドバンテージ社)が「deepinsider.jp」というサイトから、内容を改変することなく、そのまま「@IT」へと転載したものです。このため用字用語の統一ルールなどは@ITのそれとは一致しません。あらかじめご了承ください。
画像認識とは
コンピューター上では画像は単なる数値情報であり、それ以上でもそれ以下でもない。しかし人間にとって画像は豊かな情報を持っており、例えば以下の画像を見て、どのような画像であるかを考えてみてほしい。
恐らくほとんどの読者は、「真ん中に青い花が写っていて、その花の名前は“Bluebonnet”という名前である」と読み取ったのではないだろうか。今、カギ括弧で示したことには、次に示すような実に多くの処理が含まれる。
- 画像の中央部に対象となる物体がある
- その物体は青い花である
- 右下部に文字列が含まれる
- その文字列は“Bluebonnet”である
- その文字列は中央部の物体と同一のものを表している
単なる数字にすぎない画像データから、上記のような人間にとって意味のある情報を抽出するタスクのことを画像認識という。
上記でもさまざまなタスクがあるように、画像認識は一般に容易ではない。しかし最近では、深層学習を中心とした機械学習の発展により、十分なデータ量の準備と適切な問題定義ができれば、精度よく画像認識が行えるようになってきている。
【コラム】画像形式について
コンピューター上で扱える画像の形式には、
- ベクター画像形式
- ラスター画像形式
の2種類がある。
ベクター画像は、線や曲線といった図形集合の重ね合わせをデータとして保持した形式である。一方、ラスター画像はピクセル(画素ともいう)と呼ばれる色の数値を格子状に並べたデータを保持した形式である(図ex1)。勘のよい読者は格子状のデータと聞いてテンソルを思い浮かべるかもしれないが、まさにラスター画像はテンソルである。
本稿では特に断りのない限り、画像はラスター画像形式のことを指す。ピクセルが保持するデータはRGB(赤、緑、青)の三原色を各8 bits(256階調)の計24 bitsの数値で保持するものとする(図ex2)。画像サイズを W × Η とすると、画像を表すテンソルはサイズが W × Η × 3 で、R/G/Bの各要素のデータ型が8 bitsである。
CNNとは
「画像の深層学習」と言えばCNNというくらいメジャーな手法である。CNNはConvolutional Neural Networkの頭文字を取ったもので、ニューラルネットワークに「畳み込み」という操作を導入したものである。
CNNにおける画像処理の要素技術
CNNの話に入る前に、CNNで利用される画像処理の要素技術について説明する。
畳み込み
畳み込み(convolution)とは、画像処理でよく利用される手法で、カーネル(またはフィルター)と呼ばれる格子状の数値データと、カーネルと同サイズの部分画像(ウィンドウと呼ぶ)の数値データについて、要素ごとの積の和を計算することで、1つの数値に変換する処理のことである*1。この変換処理を、ウィンドウを少しずつずらして処理を行うことで、小さい格子状の数値データ(すなわちテンソル)に変換する。
言葉で説明しても分かりづらいので、具体例を出して説明しよう。今回は図2のような32×32ピクセルの画像を用意した。図1の中央の花を切り出してグレースケール化したものである。グレースケール化するとR/G/Bの数値は同一になるので、「32×32×1のテンソル」と見なせる。1ピクセルは、8bitsのデータとして0〜255の値をとる。
図2を具体的に数値表現したものが以下の図3である。すべて記述すると大きすぎるので、左上の10×10ピクセルだけを取り出している。
ここでは図4のような5×5のカーネルを考える。
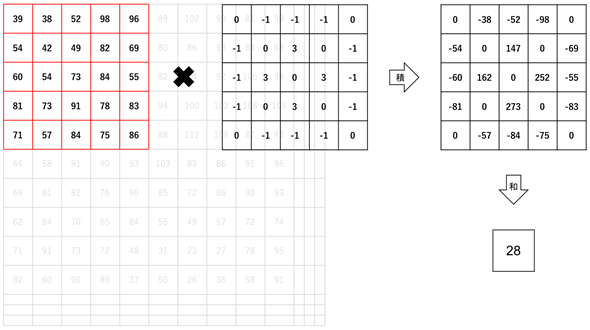
まず元の画像の左上からカーネルと同サイズ(5×5)のウィンドウを取り出し、要素同士を掛け合わせた後、それらをすべて合計して1つの数値を計算する(図5)。この場合は28となる。
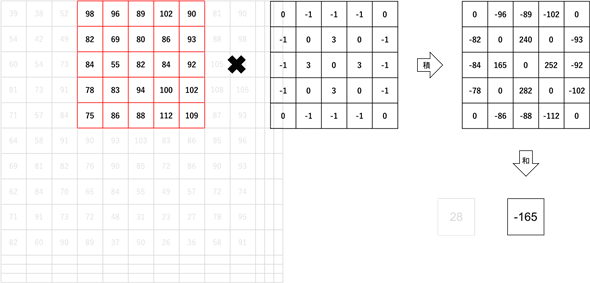
次に、抽出するウィンドウを右に3ピクセル少しずらして新しく1つの数値を計算する(図6)。2つ目の数値は-165となる。
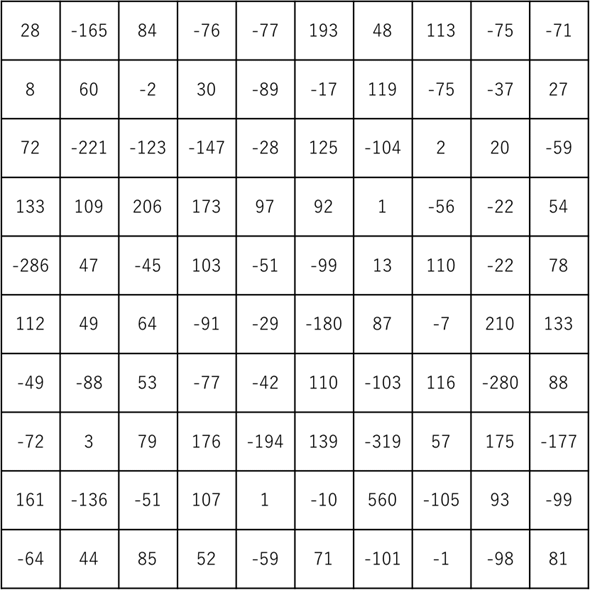
同じように右に3ピクセルずらして計算していくと、1行で10個の数値データができる。右端に到達したらまた一番左端に戻り、下に3ピクセルずらして同様に右にずらしながら計算していく。すると最終的には10×10の数値が計算される。実際に計算したのが図7だ。
このように、畳み込みを行うことで、32×32のピクセルが10×10のピクセルに縮小された。この例では5×5のカーネルを3ピクセルずつずらしながら畳み込みを行っていったが、カーネルの中身を変えたり、カーネルのサイズやずらすピクセル幅を変えたりすることで、異なる結果を得ることができる。なお、このウィンドウをずらす操作のことをストライドと呼ぶ。
畳み込みの結果はテンソルであり、テンソルは画像のようなものだ。畳み込みの結果で得られた1ピクセルは、複数のピクセルの数値情報を組み入れて計算した結果であるから、単一の数値情報であるが畳み込みに利用したウィンドウが持つ特徴的な数値を示すことになる。畳み込みによって得られたテンソルを特徴マップ(Feature map)と呼ぶ。特徴マップは名前の通り、カーネルにより抽出された特徴的な量であり、カーネルによってさまざまな情報を作り出すことができるが、本稿では深入りしない。
畳み込みはよく使われる処理なので、TensorFlowには専用の演算(tf.nn.conv2dメソッド)が用意されている。図2の画像を読み込み、図4のカーネルを利用して畳み込みを行って、図7の結果を得るまでのコードは次の通りである。なお、図2は説明のために拡大しているが、実際にサンプルコードを実行する場合は(03-02-original.png)をダウンロードして利用すること。
import tensorflow as tf
sess = tf.InteractiveSession()
# 画像をグレースケールで読み込み、浮動小数点数データに変換する
png = tf.read_file('03-02-original.png')
image = tf.image.decode_png(png, channels=1, dtype=tf.uint8)
image_float = tf.to_float(image)
# tf.nn.conv2dメソッドを適用するために4階のテンソルに変換
image_reshape = tf.reshape(image_float, [-1, 32, 32, 1])
# カーネルの作成
kernel = tf.constant(
[
[ 0, -1, -1, -1, 0],
[-1, 0, 3, 0, -1],
[-1, 3, 0, 3, -1],
[-1, 0, 3, 0, -1],
[ 0, -1, -1, -1, 0]
],
dtype=tf.float32)
# tf.nn.conv2dメソッドを適用するために4階のテンソルに変換
kernel_reshape = tf.reshape(kernel, [5, 5, 1, 1])
# ストライド幅
# 3ピクセルずつ動かす
strides = [1, 3, 3, 1]
# 畳み込み
convolution_result = tf.nn.conv2d(
image_reshape,
kernel_reshape,
strides=strides,
padding='VALID'
)
# 結果を見やすいように2階のテンソル(行列)に変換
tf.reshape(convolution_result, [10, 10]).eval()
上記のようなPythonコードはJupyter Notebook上で実行すればよい(※ちなみに、Jupyter Notebookのセルの実行中はIn [*]のように表示され、実行完了するとIn [1]のように表示されるので、実行中かどうかはここで見分けるとよい。今後の実行に必要なので、ぜひ覚えておいてほしい。)。リスト1を実行すると、図7と同じ結果を得ることができる(リスト2)。
array([
[ 28., -165., 84., -76., -77., 193., 48., 113., -75., -71.],
[ 8., 60., -2., 30., -89., -17., 119., -75., -37., 27.],
[ 72., -221., -123., -147., -28., 125., -104., 2., 20., -59.],
[ 133., 109., 206., 173., 97., 92., 1., -56., -22., 54.],
[-286., 47., -45., 103., -51., -99., 13., 110., -22., 78.],
[ 112., 49., 64., -91., -29., -180., 87., -7., 210., 133.],
[ -49., -88., 53., -77., -42., 110., -103., 116., -280., 88.],
[ -72., 3., 79., 176., -194., 139., -319., 57., 175., -177.],
[ 161., -136., -51., 107., 1., -10., 560., -105., 93., -99.],
[ -64., 44., 85., 52., -59., 71., -101., -1., -98., 81.]],
dtype=float32)
リスト1について若干の補足を加えておく。
下の方にあるtf.nn.conv2dメソッドは、その名前から行列データ(2階のテンソル)を引数にとると思うかもしれないが、畳み込まれる対象(image_reshape)とカーネル(kernel_reshape)のいずれも4階のテンソルを引数にとる。
畳み込まれる対象のテンソルの4階はそれぞれ、
- バッチサイズ*2
- 画像横幅
- 画像縦幅
- チャンネル*3
を表す。また、カーネルのテンソルの4階は、
- 横幅
- 縦幅
- 入力チャンネル*3
- 出力チャンネル*3
を表す。
*2 バッチサイズについては後で説明する。
*3 チャンネルとは、ピクセルにおけるデータサイズのことを表す。RGBデータであれば色を表すチャンネル(カラーチャンネル)が3つあることになる。グレースケールならチャンネル数は1になる。色以外のデータを表すケースもある。
上の方にあるtf.read_fileメソッドは、その名の通りファイルシステムからファイルの内容(バイト列)を取得する。通常はバイト列のまま扱うことはなく、CSVや画像などをテンソルに変換(デコード)する処理を行う。
ここではPNG画像を読み込んでおり、これをテンソルに変換するためにtf.image.decode_pngメソッドを利用している。読み込んだPNG画像はグレースケール化しているので、どのピクセルにおいてもRGBの各チャンネルの値は同一であるため、チャンネル数(channels引数)を1としている。
カーネルのサイズとストライド幅の設定によっては、画像全体をうまく網羅できない場合がある。例の32×32の画像、5×5のカーネルにおいて、ストライド幅を2とした場合を考えてみてほしい。
- 最初のウィンドウの左上の座標 (1,1) からストライド幅2で右に2ピクセルずらすと、ウィンドウの左上の座標は (3,1) となる。
- 同様にずらしていくと、ウィンドウの左上の座標 (27,1) のときは右上の座標が (31,1) となり、右端の1ピクセルが余ってしまう。
- さらに2ピクセルずらすと、今度はウィンドウの左上の座標は (29,1) で右上の座標は (33,1) となり、画像をはみ出てしまう。
このような場合、カーネルのサイズやストライド幅を調整するか、パディングと呼ばれる画像の周りに適当な数値の余白ピクセルを追加する場合がある。パディングなしの畳み込みに比べてパディングありの畳み込みは、画像の端のピクセルが利用される回数が多くなり、画像の端の特徴をよく捉えることができる。
パディングで埋める数値に指定はないが、ゼロパディングといって、画像の周りに数値0を埋める処理を行う場合が多い。TensorFlowでは、tf.nn.conv2dメソッドのpadding引数に'SAME'を指定することで(リスト3)*4、ゼロパディングを行うことができる。
*4 ちなみに、前掲のリスト1のようにパディングをしない場合は、padding引数に'VALID'を指定する。
# ゼロパディングありの畳み込み
convolution_result_with_padding = tf.nn.conv2d(
image_reshape,
kernel_reshape,
strides=strides,
padding='SAME'
)
# ゼロパディングで画像サイズが変わっているため結果のサイズも異なる
tf.reshape(convolution_result_with_padding, [11, 11]).eval()
リスト3を実行すると、図7よりも画像の端の特徴を捉えた結果を得ることができる(リスト4)。
array([
[ 76., 238., 221., 321., 194., 326., 346., 115., 166., 99., 386.],
[ 196., -16., 53., 27., 32., 62., 53., -168., -17., 174., 65.],
[ 254., -57., -115., -9., 59., 6., 88., 101., -45., 25., 140.],
[ 301., -68., -122., 70., 161., -190., 4., 74., -174., -109., 233.],
[ 94., 89., 6., 23., 91., -119., -131., -57., 328., 41., 119.],
[ 117., 76., 38., -165., -163., 141., 90., 44., 29., 53., 30.],
[ 236., -44., 79., 53., 1., 49., -46., 145., -101., -76., 59.],
[ 408., -203., 8., 85., -46., 43., -26., -259., 109., -97., 97.],
[ 136., 143., -26., -101., 35., -5., 359., 339., -167., -127., 89.],
[ 310., -71., -69., 110., -184., -75., -201., 9., -74., 4., 282.],
[ 327., 259., 149., 80., 167., 212., 161., -24., 381., 111., 223.]],
dtype=float32)
プーリング
畳み込みに似た処理で、プーリング(pooling)という処理がある。プーリングとは、ウィンドウの数値データから1つの数値を作り出す処理だ。例えばウィンドウ中の最大値を選択する最大値プーリングや、ウィンドウ中の平均値を選択する平均値プーリングなどがある。最もよく使われるのは最大値プーリングだ。
プーリングについてもTensorFlowの演算を利用すればよい。例えば最大値プーリングを行うには、tf.nn.max_poolメソッドを用いる。次のリスト5は、リスト1で作成したconvolution_resultに対してウィンドウサイズ2×2とストライド幅2で最大値プーリングを行うコードだ。リスト6はその結果。
# 最大値プーリング
pooling_result = tf.nn.max_pool(
convolution_result,
ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1],
padding='VALID'
)
# 出力用のサイズ調整
tf.reshape(pooling_result, [5, 5]).eval()
array([[ 60., 84., 193., 119., 27.],
[133., 206., 125., 2., 54.],
[112., 103., -29., 110., 210.],
[ 3., 176., 139., 116., 175.],
[161., 107., 71., 560., 93.]], dtype=float32)
逆畳み込み、アンプーリング
畳み込みやプーリングといった操作で、画像の縮小が行える。
逆に、畳み込みの逆操作(逆畳み込み: deconvolution)やプーリングの逆の処理(アンプーリング: unpooling)を行い、テンソルを拡大する操作を行う場合もある。テンソルを拡大することにより、画像生成や特徴量の再抽出を行うことが期待できる。これらの技術は本稿では利用しないので、これ以上の説明を加えない。興味があれば各自で調べてほしい。
活性化関数
第1回でニューラルネットワークにおける活性化関数の話をした。畳み込みやプーリング処理においても、結果の特徴マップに対して活性化関数を適用することがある。
CNNの構成
本節では、CNNの全体像と、それを構成する重要な関数についての説明を行う。
CNNの全体像
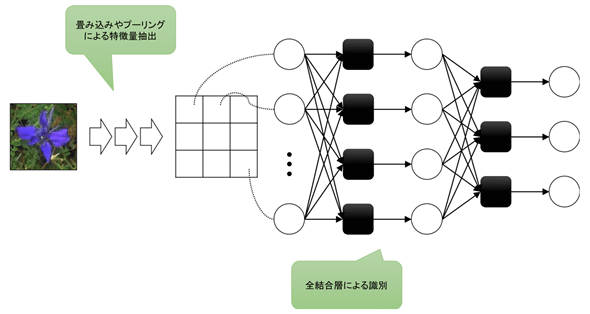
CNNは、畳み込みやプーリングによって得られた特徴マップの各ピクセルデータを、ニューラルネットワークの入力値として利用する。次の図にCNNのネットワーク構成を示す。
CNNは大きく分けて2つのパートに分けることができる。
- 1つ目は、画像を読み込み、畳み込みやプーリングによって特徴マップを作成する特徴量抽出パート
- 2つ目は、全結合層を繰り返すことで最終的な出力を得る識別パートである
最終的な出力は目的によって設定する必要があるが、例えば図中の物体が何であるかを判別したい場合は、判別対象のクラスの確率となるようにする。図8の例でいえば、最終的に3要素の出力を得るが、これがおのおの「動物である確率」「植物である確率」「それ以外である確率」となるような出力を行う。
ソフトマックス関数
ニューラルネットワークの出力は任意の数値を取り得るので、これを確率(0.0〜1.0の値)に変換しなければならない。その際に便利なのがソフトマックス関数(Softmax function)だ。ソフトマックス関数は以下のように定義される。
ここで、 pi はクラス i となる確率、 yi はニューラルネットワークの出力、 C は判別クラスの総数をそれぞれ表す。 exp(x)=ex は指数関数である。 pi が確率になる(すなわち、すべての判別クラス i についての pi が 0 < pi < 1 を満たし、かつ合計が1となる)ことは定義から明らかだろう。
ソフトマックス関数もよく利用される関数であるから、TensorFlowにはtf.nn.softmaxメソッドが用意されている。リスト7と8が、そのコード例と実行結果である。
# 仮想のニューラルネットワークの出力
y = tf.constant([1.1, 3.2, -0.9])
# ソフトマックス関数
p = tf.nn.softmax(y)
p.eval()
array([0.10750949, 0.87794065, 0.01454983], dtype=float32)
リスト8の各要素の数値を合計すると1となることに着目してほしい。ちなみにもし、その合計の計算までTensorFlowにしてほしければ、tf.reduce_sumメソッドを用いてtf.reduce_sum(p).eval()とすればよい。
CNNの注意点
CNNはあくまで畳み込み処理を利用したニューラルネットワークであり、どのくらい畳み込み処理を行うのか、どのくらいニューラルネットワークを深くするのか、といったことについては定義されていない。モデルの精度がよくなるように、ネットワーク設計者が考えたり検証したりする必要がある。どのように設計するべきかについての指針を本稿で示すことはできないが、検証の方法については次回説明する。
以上、CNNの基礎概念を説明した。次回はいよいよCNNを使って深層学習を試してみる。
【TL;DR】CNN(Convolutional Neural Network)の基礎
- 画像認識: 単なる数字にすぎない画像データから、人間にとって意味のある情報を抽出するタスク
- CNN: ニューラルネットワークに「畳み込み」という操作を導入した手法
- カーネル/フィルター: 5×5のような格子状の数値データ
- ウィンドウ: カーネルと同サイズの部分画像
- 畳み込み: ウィンドウの数値データとカーネルの積の和により1つの数値を計算する処理を、ウィンドウを少しずつずらしながら全ての要素に対して行って、最終的にテンソルに変換する処理のこと
- 特徴マップ: 畳み込みによって得られたテンソル
- パディング: 画像の周りに適当な数値の余白ピクセルを追加すること。これにより、画像の端の特徴を捉える
- プーリング: ウィンドウの数値データから1つの数値を作り出す処理。画像の縮小が行える
- CNNの2つのパート: 畳み込みやプーリングにより特徴マップを作成する特徴量抽出パートと、全結合層を繰り返すことで最終的な出力を得る識別パート
- ソフトマックス関数: 任意の数値である出力を「確率値」に変換する関数。よく利用される
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

 図1 bluebonnet
図1 bluebonnet 
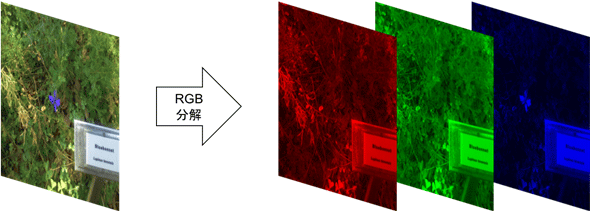
 図2 32×32ビクセルの画像
図2 32×32ビクセルの画像 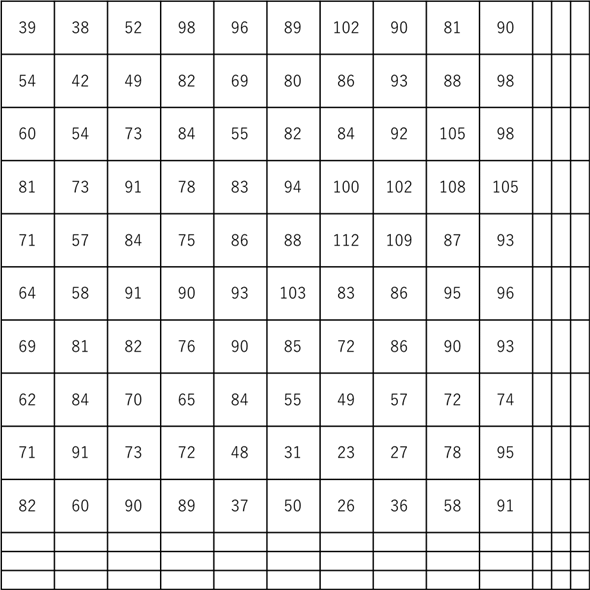
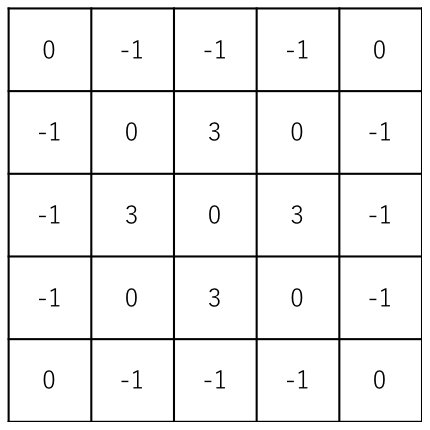 図4 5×5のサンプルカーネル
図4 5×5のサンプルカーネル