第7回 時系列データの予測を行う深層学習(RNN)を作成してみよう(TensorFlow編):TensorFlow入門(2/2 ページ)
RNNの実行(学習)
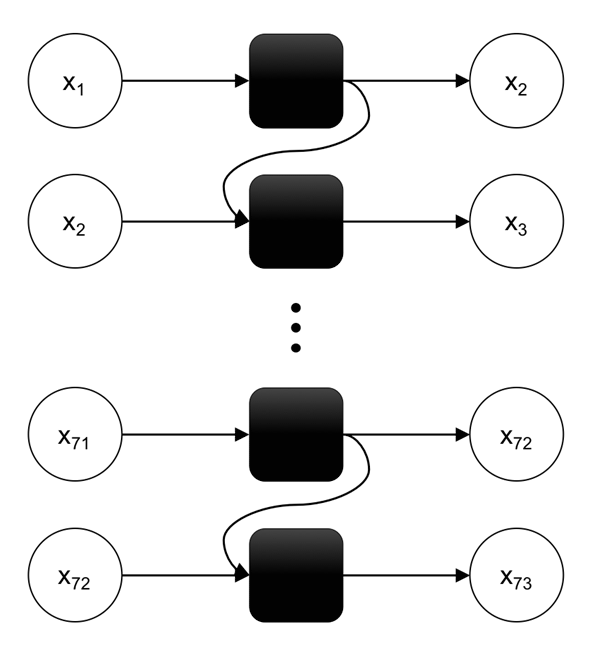
RNNの全体像を先に示す。本稿では、連続した72個のデータポイント(3日間)を用いてRNNを構築する(図3)。
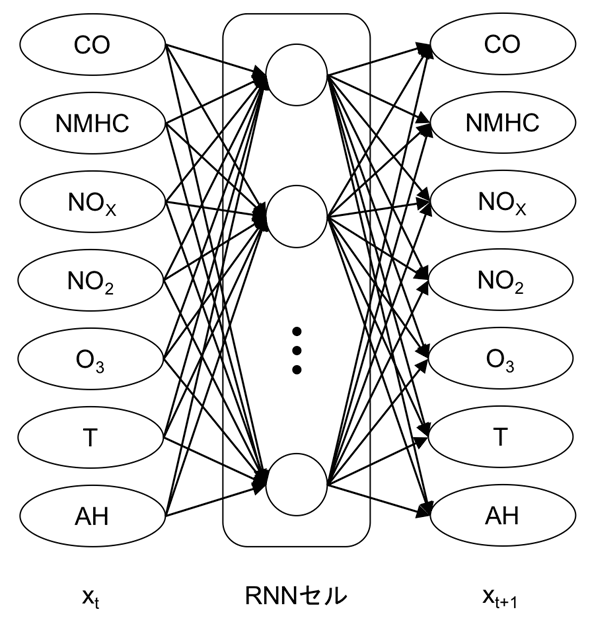
入力は時刻 t における観測値、出力は時刻 t+1 における予測値となる。RNNのセルは全結合層であり、ここでは20ニューロンとする。図4は時刻 t における入力と出力を図示したものである。最終的に出力される x73 ――すなわち入力となる連続した72時間の次の1時間のデータ――の誤差を最小化するように学習を行う。
これをコードにしていこう。まずは、TensroFlowのセッションを開始し、各種パラメーターと、データ入力用のプレースホルダーを定義する(リスト10)。
import tensorflow as tf
sess = tf.InteractiveSession()
# 再現性の確保のために乱数シードを固定
tf.set_random_seed(12345)
# パラメーター
# 学習時間長
SERIES_LENGTH = 72
# 特徴量数
FEATURE_COUNT = dataset.feature_count
# 入力(placeholderメソッドの引数は、データ型、テンソルのサイズ)
# 訓練データ
x = tf.placeholder(tf.float32, [None, SERIES_LENGTH, FEATURE_COUNT])
# 教師データ
y = tf.placeholder(tf.float32, [None, FEATURE_COUNT])
次にRNNのセルを定義する。リスト11を見てほしい。
# RNNセルの作成
cell = tf.nn.rnn_cell.BasicRNNCell(20)
initial_state = cell.zero_state(tf.shape(x)[0], dtype=tf.float32)
outputs, last_state = tf.nn.dynamic_rnn(cell, x, initial_state=initial_state, dtype=tf.float32)
前述のようにRNNのセルには、tf.rnn.rnn_cell.BasicRNNCellクラスを用いればよい。num_units引数に20(ニューロン)を指定し、activation引数は指定せずデフォルトのまま(tanh関数)とする。
RNNセルは再帰的にネットワークを構築するが、一番上のセル(tf.shape(x)[0])に対する入力が必要となる(※前掲の図3には表現されていないので注意)。つまりRNNセルの初期状態(initial_state)について定義しなければならない。ここでは単純にゼロの初期状態を与えるものとし、BasicRNNCellクラスのzero_stateメソッドを用いる。
ネットワークの入出力はtf.nn.dynamic_rnnメソッドを使う*6。tf.nn.dynamic_rnn関数の戻り値は、各セルのニューロンの状態(outputs)と、最後のセルのニューロンの状態(last_state)である。これらを用いて、おのおのの出力を求めることができる。
*6 tf.nn.static_rnn関数という関数も存在する。入力が固定長のリストである場合は、こちらを選んでもよい。tf.nn.dynamic_rnn関数は入力が可変長の場合に使われるのが本来の用途だが、そこまで厳密に気にしなくてもよいだろう。
先に示したように、今回は最終的な出力――すなわち入力の72時間の次の時間のデータ――の予測値を、最適化に利用する(リスト12)。
# 全結合
# 重み
w = tf.Variable(tf.zeros([20, FEATURE_COUNT]))
# バイアス
b = tf.Variable([0.1] * FEATURE_COUNT)
# 最終出力(予測)
prediction = tf.matmul(last_state, w) + b
# 損失関数(平均絶対誤差:MAE)と最適化(Adam)
loss = tf.reduce_mean(tf.map_fn(tf.abs, y - prediction))
optimizer = tf.train.AdamOptimizer().minimize(loss)
オプティマイザーは前々回と同じくAdamを用いる。損失関数は、平均絶対誤差(MAE:Mean Absolute Error)――つまり正解値と予測値との各変数の差(y - prediction)の絶対値(tf.abs)の平均値(tf.reduce_mean)――をとる(tf.map_fn)ことにする。
学習については前回とほとんど同じでオプティマイザーの評価を繰り返せばよいのだが、1つだけ注意すべき点がある。損失関数を「各変数の差の絶対値の平均値」としたが、[PT08.]で始まる4つの変数が1000以上の値をとりうるのに対し、[T]は高々40、[AH]にいたっては2程度である。このようなスケールの違うものについて予測して誤差を見ると、[PT08.]で始まる変数の誤差に比べて、[T]や[AH]の誤差は無視できるほど小さい。これではうまく最適化が行われない。
そこで、学習前に各変数の値を平均0、分散1に変換してスケールを揃える。この操作を標準化(Standardization)と呼ぶ。数式で表せば次のようになる。
x は個々のデータ、 μ は平均値、 σ は標準偏差である。標準化された値のことをZ値などと呼ぶこともある。
リスト8で示したTimeSeriesDataSetクラスに、標準化のためのメソッドを追加する(リスト13)。具体的には、
- mean: 平均値を求めるメソッド
- std: 標準偏差を求めるメソッド
- standardize: 標準化を行うメソッド
を新たに追加している。standardizeメソッドが、引数に平均値meanと標準偏差stdをとるようにしているが、これは訓練時ではなく、検証時に訓練時と同じ平均値と標準偏差を用いて標準化するためである。
class TimeSeriesDataSet:
……省略(リスト8参照)……
def mean(self):
return self.series_data.mean()
def std(self):
return self.series_data.std()
def standardize(self, mean=None, std=None):
if mean is None:
mean = self.mean()
if std is None:
std = self.std()
return TimeSeriesDataSet((self.series_data - mean) / std)
学習を実行するコードは次の通り。標準化を行っているところを除き、前回と大きく変わっているところはないはずだ。
# バッチサイズ
BATCH_SIZE = 16
# 学習回数
NUM_TRAIN = 10_000
# 学習中の出力頻度
OUTPUT_BY = 500
# 標準化
train_mean = train_dataset.mean()
train_std = train_dataset.std()
standardized_train_dataset = train_dataset.standardize()
# 学習の実行
sess.run(tf.global_variables_initializer())
for i in range(NUM_TRAIN):
batch = standardized_train_dataset.next_batch(SERIES_LENGTH, BATCH_SIZE)
mae, _ = sess.run([loss, optimizer], feed_dict={x: batch[0], y: batch[1]})
if i % OUTPUT_BY == 0:
print('step {:d}, error {:.2f}'.format(i, mae))
ここまでできたら、上から順番に実行してネットワークに学習させ、モデルを作成しよう。
RNNの実行(予測)
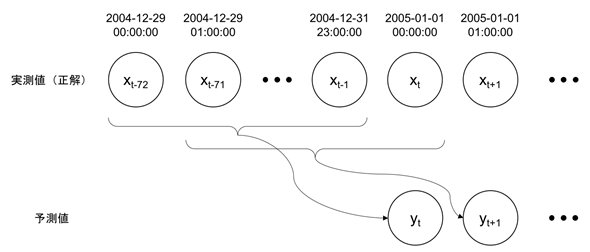
それでは、学習済みのモデルを用いて予測を行う。予測は、「予測対象となる時刻の前72時間のデータを入力データとして予測する」という操作を繰り返して行う(図5)。
前述の通り、入力データは学習時データ(2004年のデータ)の平均値と標準偏差を用いて標準化を行う。RNNの出力を、標準化操作と同じ平均値と標準偏差を用いて標準化の逆操作を行えば予測値を求めることができる。具体的には、次のコードになる。
def rnn_predict(input_dataset):
# 標準化
previous = TimeSeriesDataSet(input_dataset).tail(SERIES_LENGTH).standardize(mean=train_mean, std=train_std)
# 予測対象の時刻
predict_time = previous.times[-1] + np.timedelta64(1, 'h')
# 予測
batch_x = previous.as_array()
predict_data = prediction.eval({x: batch_x})
# 結果のデータフレームを作成
df_standardized = pd.DataFrame(predict_data, columns=input_dataset.columns, index=[predict_time])
# 標準化の逆操作
return train_mean + train_std * df_standardized
predict_air_quality = pd.DataFrame([], columns=air_quality.columns)
for current_time in test_dataset.times:
predict_result = rnn_predict(air_quality[air_quality.index < current_time])
predict_air_quality = predict_air_quality.append(predict_result)
結果が分かりやすいように、予測結果を可視化しよう。可視化の方法については、リスト16を参考にしてほしい(詳細は前掲のコラムを参照)。
# インポート&実行済みの場合、以下の3行はなくてもよい
import pandas as pd
import cufflinks as cf
cf.go_offline()
# 正解データと予測データ
correct_2005_year = dataset[dataset.times.year >= 2005].series_data
predict_2005_year = predict_air_quality
# 2005年3月分のデータに絞るには、コメントアウトを外す
#dt_2005march = pd.date_range('20050301','20050401', freq="H")
#correct_2005_year = correct_2005_year.reindex(dt_2005march)
#predict_2005_year = predict_2005_year.reindex(dt_2005march)
for feature in air_quality.columns:
plot_data = pd.DataFrame({
'正解': correct_2005_year[feature],
'予測': predict_2005_year[feature]
}).iplot(
asFigure = True,
title = feature
)
plot_data['layout']['paper_bgcolor'] = '#FFFFFF'
plot_data.iplot()
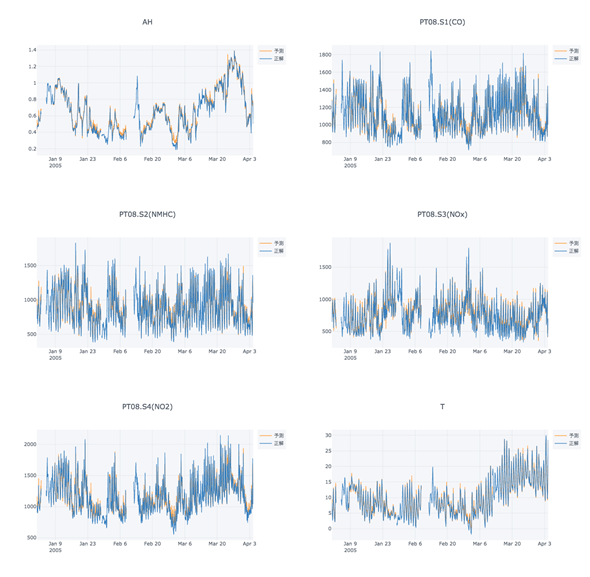
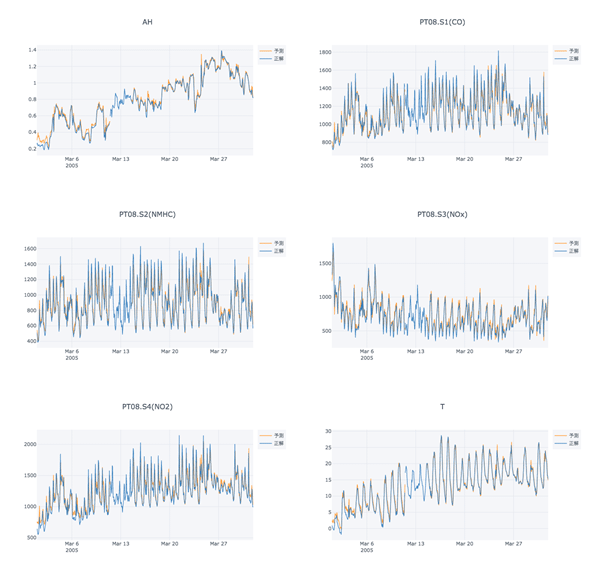
以下がリスト16を実行した例である。図6は2005年全体、図7は見やすいように2005年3月のみを抽出している。欠損値がある部分については予測が行えていないが、そうでない部分に関しては精度良く予測できている様子が見える。
余裕がある読者は、1時間先を予測するだけではなく、数時間先(例えば12時間)まで予測してみてほしい。2時間先のデータを予測するためには、まず1時間先を予測し、この予測値を入力値として利用すればよく、同様に繰り返していけば任意の未来の時間まで予測ができる。どうしても分からなければ、以下のコードをヒントにしてほしい。6時間先までを予測するサンプルコードである。
from functools import reduce
import re
# インポート&実行済みの場合、以下の3行はなくてもよい
import pandas as pd
import cufflinks as cf
cf.go_offline()
##############################################
def rnn_predict(input_dataset, ahead=1):
# 標準化
buffer = TimeSeriesDataSet(input_dataset).tail(SERIES_LENGTH).standardize(mean=train_mean, std=train_std)
# 予測対象の時刻
last_time = buffer.times[-1]
# 予測
predict_data = []
for i in range(0, ahead):
batch_x = buffer.tail(SERIES_LENGTH).as_array()
result_array = prediction.eval({x: batch_x})
predict_data.append(result_array)
buffer.append(result_array)
predict_data = reduce(lambda acc, x: np.concatenate((acc, x)), predict_data)
# インデックス時刻の作成
hour = np.timedelta64(1, 'h')
first_predict_time = input_dataset.index[-1] + hour
index = np.arange(first_predict_time, first_predict_time + ahead * hour, step=hour)
# 結果のデータフレームを作成
df_standardized = pd.DataFrame(predict_data, columns=input_dataset.columns, index=index)
# 標準化の逆操作
return train_mean + train_std * df_standardized
###############################################
predict_air_quality_1 = pd.DataFrame([], columns=air_quality.columns)
predict_air_quality_2 = pd.DataFrame([], columns=air_quality.columns)
predict_air_quality_3 = pd.DataFrame([], columns=air_quality.columns)
predict_air_quality_4 = pd.DataFrame([], columns=air_quality.columns)
predict_air_quality_5 = pd.DataFrame([], columns=air_quality.columns)
predict_air_quality_6 = pd.DataFrame([], columns=air_quality.columns)
for current_time in dataset.times[dataset.times.year >= 2005]:
# 6時間先まで予測(結果は6レコード)
predict_result = rnn_predict(air_quality[air_quality.index < current_time], 6)
# 1時間先の予測レコード
predict_air_quality_1 = predict_air_quality_1.append(predict_result[0:1])
# 2時間先の予測レコード
predict_air_quality_2 = predict_air_quality_2.append(predict_result[1:2])
# 3時間先の予測レコード
predict_air_quality_3 = predict_air_quality_3.append(predict_result[2:3])
# 4時間先の予測レコード
predict_air_quality_4 = predict_air_quality_4.append(predict_result[3:4])
# 5時間先の予測レコード
predict_air_quality_5 = predict_air_quality_5.append(predict_result[4:5])
#6時間先の予測レコード
predict_air_quality_6 = predict_air_quality_6.append(predict_result[5:6])
# 1つのデータフレームにまとめる
predict_air_quality = pd.concat(
[
dataset[dataset.times.year >= 2005].series_data,
predict_air_quality_1,
predict_air_quality_2,
predict_air_quality_3,
predict_air_quality_4,
predict_air_quality_5,
predict_air_quality_6
],
axis='columns'
)
labels = ['正解', '予測(1時間)', '予測(2時間)', '予測(3時間)', '予測(4時間)', '予測(5時間)', '予測(6時間)']
predict_air_quality.columns = ['{}_{}'.format(x, y) for y in labels for x in air_quality.columns]
###############################################
for feature in air_quality.columns:
columns_regex = '^{}_'.format(re.escape(feature))
plot_data = predict_air_quality.filter(regex=columns_regex).iplot(
asFigure = True,
title = feature
)
plot_data['layout']['paper_bgcolor'] = '#FFFFFF'
plot_data.iplot()
チューニングのための情報
RNNの応用
今回は、基本的なRNNの予測のみで良い結果が得られたためチューニングは特に行わないが、チューニングのための情報としていくつか記しておく。
今回用いたBasicRNNCellは単純なニューラルネットワークの隠れ層であったが、このセルを複雑なものに変更することもできる。例えば単純なRNNは長期依存の時系列(ある時点における出力が、その時点よりかなり前の時点の入力に依存するもの)についての学習はうまくいかないことが知られている。この欠点を解決する方法としてLong Short-Term Memory(LSTM)という手法がある。
LSTMは、RNNと同様に特定の入出力の構造を繰り返す。LSTMの構造は本稿では説明しないが、TensorFlowでLSTMを用いるには、tf.nn.BasicRNNCellクラスと同様に、tf.nn. rnn_cell.BasicLSTMCellクラスを使えばよい。
RNNのキモは「繰り返し構造をどのように構築するか」ということになるが、LSTMを始めとしてさまざまな手法が提案されている。TensorFlowにも多くのセルが提供されているので、公式ドキュメントの「RNN and Cells」を参考にしてみるとよいだろう。
次回は本連載の最終回として、TensorFlowを活用する際に役立つ「TensorBoard」というツールを紹介する。今回のプログラムとデータは、次回で再利用するので消さずに保存しておいてほしい。
【TL;DR】時系列データの予測
- tf.nn.rnn_cell.BasicRNNCellクラス: 単純なRNNのモデルを作成できるクラス
- tf.nn.rnn_cell.BasicLSTMCellクラス: セルが複雑なRNN(LSTM)のモデルを作成できるクラス
- Air Qualityデータセット: センサーデバイスにより収集された大気質の時系列データセット。手動でダウンロードする必要がある
- pandasパッケージ: データ解析用Pythonライブラリ。時系列データの解析やグラフ図生成によるデータの可視化などが行える
- xlrdパッケージ: Excelデータを読む込むためのPythonライブラリ
- Cufflinksパッケージ: データフレームを簡単にグラフとして可視化できるパッケージ。データの可視化をサポートするプラットフォーム&パッケージであるPlotlyをバックエンドに使用
- プロット: データを可視化すること、もしくは可視化されたグラフのこと
- RNNにおける訓練データ: 時系列データの学習では、連続したデータポイントを訓練データとする。今回は連続したデータポイントをランダムに切り出すためのnext_batchメソッドを自作している
- データ分割: 今回はデータセットを、訓練(train)データと、精度検証用のテスト(test)データに分離する
- RNNのセル: tf.rnn.rnn_cell.BasicRNNCellクラスを使用。全結合層で、今回は「20」ニューロンとした
- 損失関数とオプティマイザー: 平均絶対誤差(MAE:Mean Absolute Error)とAdamを使用した
- 標準化: 学習前に各変数の値を平均「0」、分散「1」に変換して、値のスケールを揃えるテクニック
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ