MNISTの手書き数字を全結合型ニューラルネットワークで処理してみよう：作って試そう！ ディープラーニング工作室（2/2 ページ）

[かわさきしんじ，Deep Insider編集部]

ニューラルネットワーククラスの定義

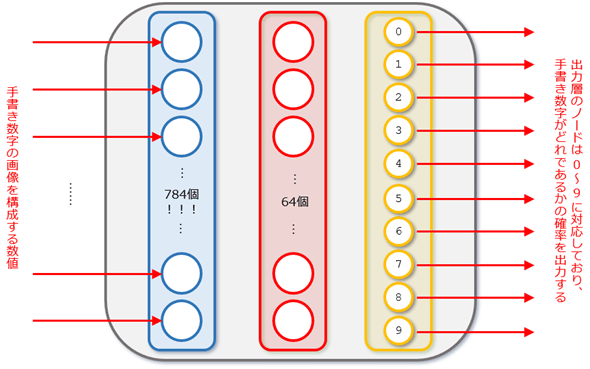
　「ニューラルネットワーククラスを定義してみましょう」とはいってみましたが、ここでは全結合を行うシンプルなニューラルネットワークを定義します。ここでは入力層は784個（28×28個）のノードを持ち、隠れ層のノード数は64個、出力層のノード数は10個とします。

ここで定義するニューラルネットワーククラス

　入力の数こそ多いのですが、これはあやめの品種の分類と同様に多クラス分類と呼ばれる処理です。出力が10個なのは、推測結果（0〜9）に応じて、対応するノードが一番大きな数値を出力するようにするためです。

推測結果	モデルからの理想的な出力	対応する正解ラベル
0	1, 0, 0, 0, 0, 0, 0, 0, 0, 0	0
1	0, 1, 0, 0, 0, 0, 0, 0, 0, 0	1
2	0, 0, 1, 0, 0, 0, 0, 0, 0, 0	2
3	0, 0, 0, 1, 0, 0, 0, 0, 0, 0	3
4	0, 0, 0, 0, 1, 0, 0, 0, 0, 0	4
5	0, 0, 0, 0, 0, 1, 0, 0, 0, 0	5
6	0, 0, 0, 0, 0, 0, 1, 0, 0, 0	6
7	0, 0, 0, 0, 0, 0, 0, 1, 0, 0	7
8	0, 0, 0, 0, 0, 0, 0, 0, 1, 0	8
9	0, 0, 0, 0, 0, 0, 0, 0, 0, 1	9
推測結果とニューラルネットワークモデルの計算結果と正解ラベル

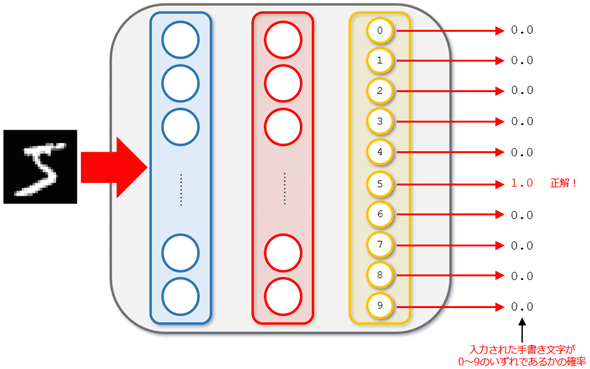
　つまり、以下のようなニューラルネットワークモデルを作ることが目標です。ただし、以下で見ていくコードではソフトマックス関数と呼ばれる関数を使っていません。この関数は各ノードからの出力値の合計値が1.0となる、つまり、各ノードからの出力値を確率として捉えられるような値を返す活性化関数ですが、これを使っていないので、実際には最大の値を出力したノードが、ニューラルネットワークが推測した数字であると判断をしています（各ノードの出力値の中で最大値のものがやはりソフトマックス関数を通したときに、最大の確率のとなるので、ここではそれでよしとしましょう）。

こんな出力になるのが理想

　基本的な形は、前回までに定義したものと同じです。そのため、コードも見慣れたものになっています。

class Net(torch.nn.Module):
    def __init__(self, INPUT_FEATURES, HIDDEN, OUTPUT_FEATURES):
        super().__init__()
        self.fc1 = torch.nn.Linear(INPUT_FEATURES, HIDDEN)
        self.fc2 = torch.nn.Linear(HIDDEN, OUTPUT_FEATURES)
        #self.softmax = torch.nn.Softmax(dim=1)
    def forward(self, x):
        x = self.fc1(x)
        x = torch.nn.functional.relu(x)
        x = self.fc2(x)
        #x = self.softmax(x)
        return x

全結合型で手書き数字を認識するニューラルネットワーククラス

　これまでに見てきたコードと異なるのは、インスタンス生成時にパラメーターに、入力層のノード数、隠れ層のノード数、出力層のノード数を受け取るようにしたことと、活性化関数にReLUを使用しているところくらいです（__init__メソッドとforwardメソッドの最後では先ほど述べたようにtorch.nn.Softmax関数に関連するコードをコメントとして記述していますが、後述する損失関数の内部で同様な処理が行われるので、ここでは省略しています。興味のある方は試してみてください）。

　それ以上の説明は不要でしょう。というわけで、次に実際に学習をするコードを見てみます。

学習とテスト

　実際に学習を行うコードの基本形もこれまでに見てきたものとあまり変わりません。

　まずは上で定義したNetクラスのインスタンスを生成します。

INPUT_FEATURES = 28 * 28
HIDDEN = 64
OUTPUT_FEATURES = 10

net = Net(INPUT_FEATURES, HIDDEN, OUTPUT_FEATURES)

Netクラスのインスタンスを生成

　次に損失関数と最適化アルゴリズムを選択します。今回は、損失関数に多クラス分類でよく使われるtorch.nn.CrossEntropyLossクラスを使っています。PyTorchではCrossEntropyLossクラスのインスタンスを使って、損失を計算するときには、出力値（10個の浮動小数点数値を要素とするテンソル）と、その中で値が最大の要素を指すインデックスを渡すことになっています。そして、先ほど見たように、正解ラベルはまさに数字を表すインデックス値になっていたことを思い出してください。実際に、以下のコードではそのようにしているのが分かります（この関数の内部では、実際にはソフトマックス関数の一種が使われるため、Netクラスの定義にはこれを含めていません）。

import torch.optim as optim

criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)

損失関数と最適化アルゴリズムの選択

　PyTorchのCrossEntropyLoss関数による損失の計算方法などについては、後続の回で取り上げるタイミングがあれば、そこで紹介します。

　それでは、最後に学習を行うコードを示します。

EPOCHS = 2

for epoch in range(1, EPOCHS + 1):
    running_loss = 0.0
    for count, item in enumerate(trainloader, 1):
        inputs, labels = item
        inputs = inputs.reshape(-1, 28 * 28)

        optimizer.zero_grad()
        outputs = net(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if count % 500 == 0:
            print(f'#{epoch}, data: {count * 20}, running_loss: {running_loss / 500:1.3f}')
            running_loss = 0.0

print('Finished')

学習を行うコード

　注意点としては、あやめの品種の分類では全てのデータをニューラルネットワークに入力していましたが、今回はデータの数がそれよりもはるかに多くなっています。そのため、上述したようにエポックごとに訓練データをシャッフルして、そこから20個（バッチサイズ）のデータをニューラルネットワークに入力するようになっていることが挙げられます。そのため、forループが二重になっていることに注意してください。内側のforループでは、enumerate関数を使って、trainloader経由でデータを20個取り出すと同時にカウンターの値を増やして、その後の処理で使用しています。このように小さな塊（ミニバッチ）ごとに処理を進めていく方法をミニバッチ学習と呼びます。

　また、「inputs.reshape(-1, 28 * 28)」というのは、変数inputsに取り出した画像データ（その形状は[20, 1, 28, 28]です。つまり、チャネル（1）／画像の高さ（28）／画像の幅（28）を要素とするテンソルを20個格納するテンソルです）を、入力層の784ノードに合わせて、20×784というサイズのデータに変換する操作です（「20」ではなく「-1」と指定しているのは、「28×28＝784は重要だけど、それ以外はよろしくやってください」とreshapeメソッドに丸投げすることを意味しています）。20はバッチサイズ（画像データの個数）なので、これはつまり画像の高さと幅で構成されていた2次元のデータの1次元のデータに展開したものを20個含むテンソルにする操作ということになります（チャネルは、torchvisions.transforms.ToTensorクラスを使って読み込んだデータをPyTorchのテンソルに変換する段階で自動的に付加されますが、ここでは不要な次元です）。

　変数running_lossは、20個のデータをニューラルネットワークに入力した結果を基に算出した損失を内部のループを実行するたびに加算していき、ループ変数countの値が500になった時点（つまり、500回のループ×20個＝1万個のデータを処理した時点）でその平均値を出力するために使っています。

　その他の処理はこれまでと同様です。

　実行結果を以下に示します。

実行結果

　上のコードでは、定数EPOCHSの値が2なので、2つのエポックを実行して、1つのエポックのたびに6万個のデータが使われて学習が実行されていることが分かります。損失も徐々に小さくなっていますね。

　学習が終わったところで、最後に使用した訓練データを基にした推測結果とその正解ラベルとを比べてみましょう。

_, predicted = torch.max(outputs, 1)
print(predicted)
print(labels)

最後の訓練データを基にした推測結果と正解ラベルを比較

　ここで行っている「torch.max(outputs, 1)」というのは、「各行（入力データから得られた推測値である10個の数値）の中で最大のものを選び、(最大値, そのインデックス)というタプルを返す」処理です。この呼び出しでは今述べたように、(最大値, そのインデックス)というタプルを返しますが、ここで必要なのはインデックスだけです。そのため、代入文の左辺ではアンダースコア「_」を使って、「_, predicted = ……」のようにインデックスだけを受け取っています（実際には「print(_)」のようにすれば、最大値も表示できますが、一般にアンダースコア1つだけの変数はプログラマーによる「このデータは不要です」という表明として扱われます）。

　これを実行すると次のようになります。

実行結果

　おおむねよさそうな結果になっているのが確認できました。

　最後にテストデータを使って、このニューラルネットワークモデルのテストを行ってみましょう（機械学習では、学習と評価を繰り返して、学習に関連するハイパーパラメーターの調整などを行いながら、ニューラルネットワークモデルの精度を高めて、最後にテストを行うのが常道ですが、ここでは省略します）。

correct = 0
total = 0

with torch.no_grad():
    for data in testloader:
        inputs, labels = data
        inputs = inputs.reshape(-1, 28 * 28)
        outputs = net(inputs)
        _, predicted = torch.max(outputs, 1)
        total += len(outputs)
        correct += (predicted == labels).sum().item()

print(f'correct: {correct}, accuracy: {correct} / {total} = {correct / total}')

ニューラルネットワークモデルをテストする

　2つの変数correctとtotalは、このニューラルネットワークモデルのテストで正解となった推測結果の数と処理をしたデータの総数を保存しておくために使います。その後にある、「with torch.no_grad():」というwith文は、そのブロックで行う処理では勾配の計算を無効にするものです（ここでは学習を行わずに、テストをしているので、このようにすることで無駄な処理を行わずに済むようになります）。

　with文のブロック内ではforループを使って、testloaderから20個ずつ取り出したデータをニューラルネットワークモデルに入力しています。そして、その推測結果で正しいものの数を上述した変数correctに、処理したデータの数（常に20ではありますが）を変数totalに加算していき、最後に正解の数と精度を表示するようにしました。

　実行結果を以下に示します。

実行結果

　ここでは全結合型のニューラルネットワークを作成しましたが、それでも92％程度の精度が出ていることが分かりました。とはいえ、実は画像認識を行うニューラルネットワークではもっとよい方法があることが知られています。次回以降では、その方法について取り上げていきましょう。

「作って試そう！　ディープラーニング工作室」