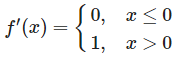[活性化関数]ReLU(Rectified Linear Unit)/ランプ関数とは?:AI・機械学習の用語辞典
用語「ReLU(Rectified Linear Unit)/ランプ関数」について説明。「0」を基点として、0以下なら「0」、0より上なら「入力値と同じ値」を返す、ニューラルネットワークの活性化関数を指す。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
用語解説
AI/機械学習のニューラルネットワークにおけるReLU(Rectified Linear Unit、「レルー」と読む)とは、関数への入力値が0以下の場合には出力値が常に0、入力値が0より上の場合には出力値が入力値と同じ値となる関数である。
図1に示すように、座標点(0, 0)を基点として、ランプ(ramp: 例えば高速道路に入るための上り坂などの「傾斜路」のこと)型曲線のグラフになるため、「ランプ関数」(ramp function)とも呼ばれる。
ニューラルネットワークの基礎となっている情報処理モデル「パーセプトロン」では「ステップ関数」という活性化関数が用いられ、「バックプロパゲーション」が登場してからは「シグモイド関数」が活性化関数として使われるようになった。
しかしディープニューラルネットワークでは、層が深くなるにつれ勾配が消えてしまう勾配消失問題(Vanishing gradient problem)が発生した。勾配が消えていく理由は、シグモイド関数の微分係数(=導関数の出力値)の最大値が0.25(範囲は0.0〜0.25)であり、そのシグモイド関数を重ねれば重ねるほど勾配の値は小さくなっていくからだ。よって、微分係数の最大値が1.0(範囲は0.0か1.0)である「ReLU」(本稿で解説)が使われるようになったというわけである。
ReLUのメリットは「勾配消失問題の解消」だけではなく、
- 計算式がシンプルなので、処理が速い
- 0以下は常に0となるので、ニューロン群の活性化がスパース(sparse: 疎、スカスカ)になり、発火しないニューロン(=生体ニューロンに近い動作)も表現できることで精度が向上しやすい
といった点もある。
主要ライブラリでは、次の関数/クラスで定義されている。
「Rectified Linear Unit」の意味について
「ReLU: Rectified Linear Unit」を訳すと、整流された線形ユニットとなる。電気工学で「整流器(rectifier)」と言うと「電流を一方向にだけ流す(=整流)機器」を指すが、同様に「整流された(Rectified)」とは「正の値だけを流し、負の値は流さないようにしている」ことを意味する。ここでの「ユニット(Unit)」は「器、箱」のような意味で「関数」と同義である。ゆえに本稿では、「ReLU」の名称には「関数」と付けていない。
「正規化線形関数」と訳されている場合もあるが、いわゆる「正規化(Normalization)」を指すわけではないので注意してほしい。
定義と数式
冒頭では文章により説明したが、厳密に数式で表現すると次のようになる。
xが入力データで、f(x)が出力結果である。
x≤0の場合は、f(x)=0となり、
x>0の場合は、f(x)=xとなる。
同じ意味になるが、max(0, x)と表現される場合もある。
上記の数式の導関数(Derivative function:微分係数の関数)を求めると、次のようになる。
ReLUはステップ関数と同様に、不連続な関数であり、数学的にはx=0の地点では微分ができない。
ReLUの導関数をニューラルネットワーク内で使うために、便宜的にx=0を微分係数0の方に含めることにする(※1に含めたり、0.5にしたりする方法もある)。これにより、次のような導関数が求まる。
Pythonコード
上記のReLUの数式をPythonコードの関数にするとリスト1のようになる。
def relu(x):
return x * (x > 0.0)
x > 0.0は「入力値が0より上か、そうではないか(=0以下か)」という条件を意味する。
その条件がTrue(=1)のときは、戻り値としてx(=x * (1))を返す。
また、その条件がFalse(=0)のときは、戻り値として0.0(=x * (0))を返す。
数値計算ライブラリ「NumPy」を使う場合は、計算部分をimport numpy as np; np.amax([0, x])と記載してもよい。
ReLUの導関数(derivative function)のPythonコードも示しておくと、リスト2のようになる。
def der_relu(x):
return 1.0 * (x > 0.0)
ここを更新しました(2024年1月15日)
「後日解説」となっていて、解説されていない部分を修正しました。
Copyright© Digital Advantage Corp. All Rights Reserved.

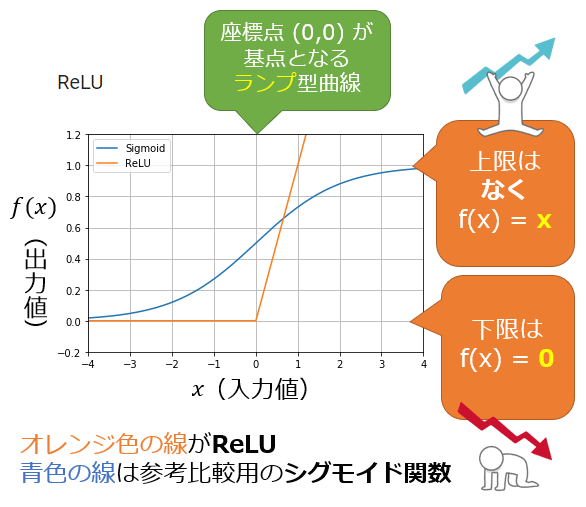 図1 「ReLU」のグラフ
図1 「ReLU」のグラフ