RNNに触れてみよう:サイン波の推測:作って試そう! ディープラーニング工作室(2/2 ページ)
RNNを使用するニューラルネットワークの定義
PyTorchにはRNN機能を提供するクラスが幾つか用意されています。今回はその中でも基本的なRNNクラス(torch.nn.RNNクラス)を使用します。このクラスと、既におなじみのLinearクラスを組み合わせることにしましょう。
実際のクラス定義のコードは次の通りです。
class Net(torch.nn.Module):
def __init__(self, input_size, hidden_size):
super().__init__()
self.rnn = torch.nn.RNN(input_size, hidden_size)
self.fc = torch.nn.Linear(hidden_size, 1)
def forward(self, x, hidden):
output, h = self.rnn(x, hidden)
output = self.fc(output[:, -1])
return output, h
__init__メソッドでは、インスタンス変数self.rnnにRNNクラスのインスタンスを代入しています。RNNクラスのインスタンス生成時には「torch.nn.RNN(input_size, hidden_size)」のように「入力のサイズ」と「隠れ状態のサイズ」の2つの引数を指定しています(これらは__init__メソッドのパラメーターに渡されるようにしてあります)。
ここで覚えておいてほしいのは、先ほど作成した訓練データではバッチサイズ(num_batch)として25を指定しましたが、これはここでいう「入力のサイズ」とは違うということです。このニューラルネットワークでは「一度に1つのデータを入力して、それを処理」しますが、バッチサイズの25というのは時系列のデータとしてそれらを連続的に入力するということです。先ほどの図に合わせると、次のようになります。
25個の時系列データが順次RNNに入力されると、最初に入力されたデータ(x1)はそれ以降のデータの処理に何らかの影響を与え、2番目に入力されたデータは3番目以降のデータの処理に何らかの影響を与えていくことが分かります。__init__メソッドのhidden_sizeパラメーターに値を指定して作成する隠れ状態は、次の層への出力となったり、次のデータの処理時にRNN層への入力として使われたりします。
全結合層についてはこれまでと同様ですが、PyTorchのRNNクラスと結合させる場合、その入力の数は、RNN層の隠れ状態のサイズに指定した値と同じにします。そのため、インスタンス変数self.fcに代入するLinearクラスのインスタンス生成では「torch.nn.Linear(hidden_size, 1)」としています。出力層のノード数が1なのは、これは時系列データを受け取り、そこから次のサイン波の値を1つだけ推測するからです。
なお、PyTorchのRNN層には活性化関数tanhを使った活性化処理がデフォルトで組み込まれているので、このクラス定義では明示的には活性化関数は登場しません。
forwardメソッドでは、まずパラメーターがselfを含めて3つ(実際の呼び出し時には2つを指定)ある点に注意してください。これは隠れ状態の初期値を、「net(入力, 隠れ状態の初期値)」のようにして、このクラスのインスタンスを呼び出す側が用意する必要があるということです。また、このメソッド内で行っている「self.rnn(x, hidden)」呼び出しでは受け取った入力と隠れ状態をRNNクラスのインスタンスに渡しています。その戻り値が2つある点にも注意が必要です。一つは次の層への出力に、もう一つは現在の入力をした時点での隠れ状態を表すオブジェクトになります。
また、全結合層には「self.fc(output[:, -1])」のようにして、計算結果の一部のみを渡しています。詳しくは次回以降に見ますが、これは25個の時系列データごとに出力される25個の計算結果(これは隠れ状態のサイズと同じサイズのテンソルになります)の中で最後のものだけを取り出す操作です。これを全結合層に送り込むと、最終的な計算結果、つまり「25個の時系列データを基にニューラルネットワークモデルが推測した次の値(を要素とするテンソル)」が得られるというわけです。
最後に、PyTorchのRNNクラスでは、RNNを何層にするかをインスタンス生成時に指定できます(名前付き引数num_layersで指定。デフォルト値は1です)。ここではデフォルト値を採用することにします。RNNを2層以上にする例は次回以降に紹介する予定です。
クラスの定義は以上です。次に学習をしてみましょう。
学習
今回は、学習のコードは簡略化したものとします(いわゆるミニバッチのようなことはせずに一度のforループで学習をしてみます)。
まずは、訓練データと正解ラベル、Netクラスのインスタンスを用意します。訓練データは先ほども試しに作りましたが、見通しをよくするように、ここで作り直しておきましょう。
訓練データと正解ラベルは前述した通り、make_train_data関数を呼び出すだけです。
num_div = 100
cycles = 2
num_batch = 25
X_train, y_train = make_train_data(num_div, cycles, num_batch)
次に上で定義したNetクラスのインスタンスを生成して、損失関数と最適化アルゴリズムを選択します。
input_size = 1
hidden_size = 32
net = Net(input_size, hidden_size)
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(net.parameters(), lr=0.05)
先ほども述べたように、このRNNには一度に1個のデータを入力していくので、input_sizeは1です。隠れ状態のサイズは適当に32としてあります(このサイズに合わせて、この後の隠れ状態の初期化を行います)。損失関数には、MSELoss関数を使います。これは出力層からの出力が1つだけのためだからです。最適化アルゴリズムもこれまでの回と同様です。
次に学習を行うコードを示します。
num_layers = 1
EPOCHS = 100
losses = []
for epoch in range(EPOCHS):
print('epoch:', epoch)
optimizer.zero_grad()
hidden = torch.zeros(num_layers, num_batch, hidden_size)
output, hidden = net(X_train, hidden)
loss = criterion(output, y_train)
loss.backward()
optimizer.step()
print(f'loss: {loss.item() / len(X_train):.6f}')
losses.append(loss.item() / len(X_train))
RNNには訓練データに加えて、隠れ状態の初期値を渡す必要もありました。上のコードではforループの中で「hidden = torch.zeros(num_layers, num_batch, hidden_size)」として、ループのたびにこれをリセットするようにしています。これは「RNN層の数(ここでは1)×バッチサイズ(ひとかたまりの時系列データの数。ここでは25個)×RNNクラスのインスタンス生成時に指定した隠れ状態のサイズ(ここでは32)」という形状である必要があります。そこで、ここではnu_layers、num_batch、hidden_sizeを指定して、そのようなサイズでゼロ初期化したテンソルを用意しています。
後は訓練データとこれを一緒にNetクラスのインスタンスに渡すだけです。その後のコードについては特に説明の必要はないでしょう(netインスタンスの呼び出しでは「output, hidden = net(……)」のようにして、隠れ状態の現在の状態を受け取っていますが、上のコードではループのたびにこれをリセットしているので、実際にはこれは使っていません)。変数lossesには損失をX_trainの要素数で割った値を蓄積しておき、後でこれを表示してみましょう。
実行結果を以下に示します。
学習が完了したら、損失がどんな感じかをプロットしてみましょう。
plt.plot(losses)
実行結果を以下に示します。
これは非常にシンプルな例だったので、学習にかかる時間も少なく、比較的早いうちにそれなりの損失になっているようです。ただ、問題はほんとうに推測ができているかです。そこで、最後の学習結果であるoutputに格納されている値を使って、グラフをプロットしてみましょう(上述しましたが、outputには「25個の時系列データから推測される次の値」が含まれています)。
これをプロットするコードを以下に示します。
output = output.reshape(len(output)).detach()
plt.plot(sample_data)
plt.plot(range(24, 200), output)
plt.grid()
上のコードでは、outputは推測値のみを要素とするテンソルを要素とするテンソル(2次元)になっているので、reshapeメソッドでこれを1次元のテンソルに展開しています。また、detachメソッドで勾配計算に必要だった要素を分離しています(これを行わないとグラフをプロットできません)。また、最初に作成していたsample_data(ノイズなしのサイン波のデータ)も同時にプロットするようにしました。そのため、推測値についてはグラフ上での描画開始位置を細工しています。
実行結果を以下に示します。
オレンジ色のラインがノイズなしのサイン波です。青いラインが推測値を使って描画したサイン波です(サイン波が途中から始まっているのは、X_trainの最初の25個については、推測値がないためです。興味のある方は変数num_divを増やすなどして試してみてください)。最初の部分があまりよくないのですが、そこを除けば、まあまあサイン波といってもよいでしょう。
最後に、もう少し違ったデータを推測してみましょう。ここではπ/2だけ、サイン波をオフセットしてみます(コサイン波と同じ)。
foo, bar = make_data(100, 1, np.pi / 2)
plt.plot(foo)
plt.grid()
これを実行すると次のようなグラフがプロットされます。
これに対応する訓練データをmake_train_data関数を使って作成して、今作成したニューラルネットワークモデルに入力してみます。
X_test, y_test = make_train_data(100, 1, 25, np.pi / 2)
output2, _ = net(X_test, hidden)
plt.plot(foo)
plt.plot(range(24, 100), output2.reshape(len(output2)).detach())
plt.grid()
こちらでも上のオフセットしたサイン波(ノイズなし)と、推測値から得られたグラフの両者をプロットしています。make_train_data関数にはオフセット値としてπ/2を渡していることにも注意してください。それ以外は上と同様です。
実行結果を以下に示します。
こちらについてもそれなりの近似ができているようです。
今回は取りあえずRNNに慣れてみることを目的に、さまざまな要素はすっ飛ばして、シンプルなサイン波の推測をRNNで行ってみました。次回は、このコードについて少し詳しく見ていくことにしましょう。
Copyright© Digital Advantage Corp. All Rights Reserved.

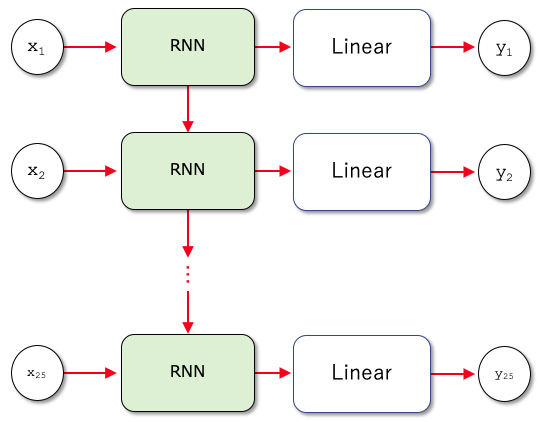 以前に入力されたデータが最後に入力されたデータにまで影響を及ぼす
以前に入力されたデータが最後に入力されたデータにまで影響を及ぼす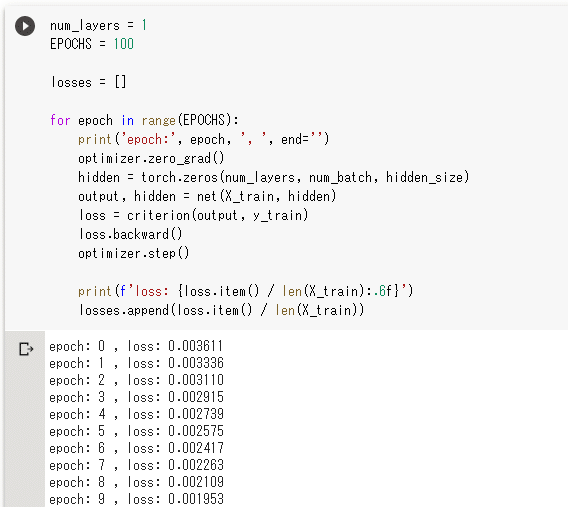 実行結果
実行結果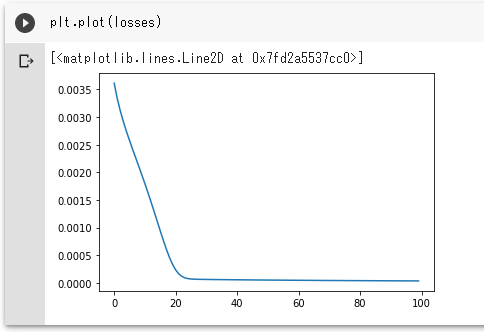 実行結果
実行結果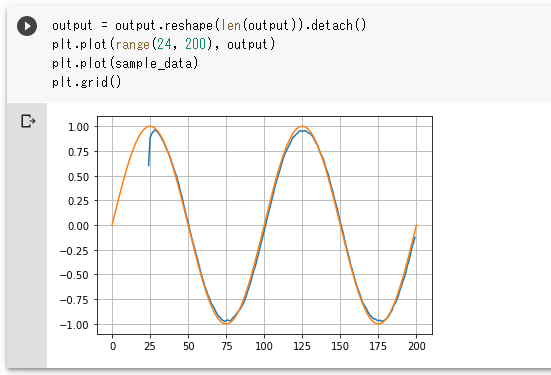 実行結果
実行結果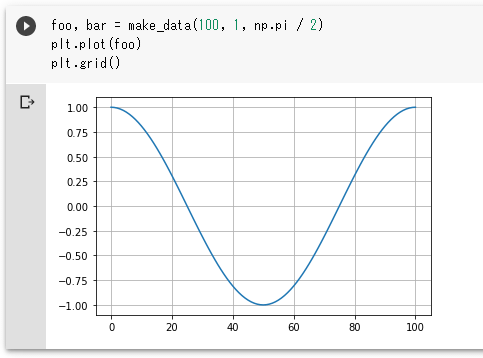 実行結果
実行結果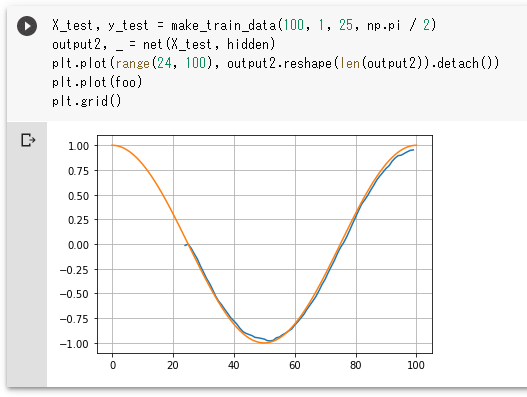 実行結果
実行結果



