[活性化関数]tanh関数(Hyperbolic tangent function: 双曲線正接関数)とは?:AI・機械学習の用語辞典
用語「tanh関数(双曲線正接関数)」について説明。座標点(0, 0)を基点(変曲点)として点対称となるS字型の滑らかな曲線で、「-1」〜「1」の間の値を返す、ニューラルネットワークの活性化関数を指す。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
用語解説
AI/機械学習のニューラルネットワークにおけるtanh関数(Hyperbolic tangent function: 双曲線正接関数、「ハイパボリックタンジェント」や「タンエイチ」と読む)とは、あらゆる入力値を-1.0〜1.0の範囲の数値に変換して出力する関数である。
図1に示すように、座標点(0, 0)を基点(変曲点)として点対称で、S(=ς:シグマ)字型曲線のグラフになる。つまり「tanh関数」は、「シグモイド関数の拡張バージョン」ともいえる活性化関数である。
ニューラルネットワークの基礎となっている情報処理モデル「パーセプトロン」(後日解説)では「ステップ関数」という活性化関数が用いられ、「バックプロパゲーション」(後日解説)が登場してからは「シグモイド関数」が活性化関数として使われるようになった。
しかしシグモイド関数の微分係数(Derivative: 導関数の出力値)の最大値は0.25と小さいため、勾配が小さくなりがちで学習に時間がかかるという問題があった。そのため学習がより高速化するように、最大値が1.0(図2)となる「tanh関数」がよく採用されるようになった。
さらに最近のディープニューラルネットワークでは、「ReLU」がよく使われるようになっている。というのも、シグモイド関数やtanh関数では勾配消失問題(後日解説)を解決できなかったが、ReLUでは(図2を見ると分かるように「入力が0.0より大きいと、常に1.0が出力される」ことによって)勾配消失問題を解決できるようになったからである。
現在では、tanh関数は、「-1.0〜1.0の数値を出力する」という特性を生かして、主に出力層で用いられている。主要ライブラリでは、次の関数/クラスで定義されている。
定義と数式
冒頭では文章により説明したが、厳密に数式で表現すると次のようになる。
eは「オイラー数」(Euler number=ネイピア数:Napier's constant、自然対数の底)と呼ばれる数学定数の一つで、約2.718281…という無理数(=小数点以下が無限に続く数)である。オイラー数は、微分計算がしやすいというメリットがある。具体的に上記の数式の導関数(Derivative function:微分係数の関数)を求めると、次のように非常にシンプルな式になる。
Pythonコード
上記のtanh関数の数式をPythonコードの関数にするとリスト1のようになる。
import numpy as np
def tanh(x):
return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
オイラー数で簡単に計算するため、ライブラリ「NumPy」をインポートしている。np.exp(x)/np.exp(-x)というコードがex/e−xという数式を表現している。expは、e(オイラー数)を底(base)とする指数関数(exponential function)を意味する。ちなみにネイピア数自体はnp.eで取得可能である。
tanh関数の導関数(derivative function)のPythonコードも示しておくと、リスト2のようになる。
# ※リスト1のコードを先に記述する必要がある
def der_tanh(x):
return 1.0 - (tanh(x) ** 2)
Copyright© Digital Advantage Corp. All Rights Reserved.

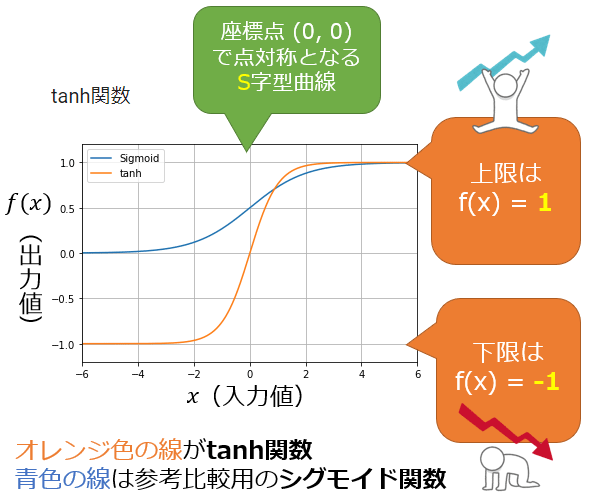 図1 「tanh関数」のグラフ
図1 「tanh関数」のグラフ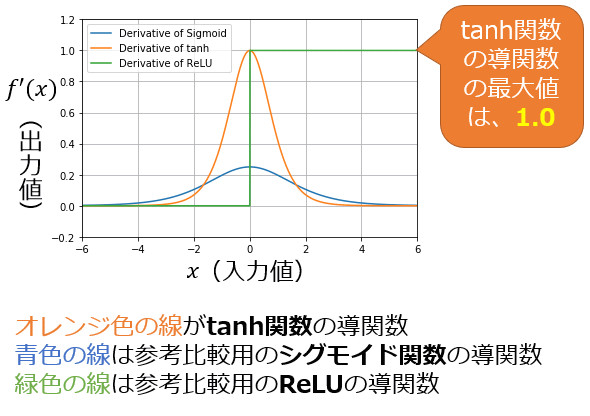 図2 シグモイド関数/tanh関数/ReLUの「導関数」(微分係数の関数)のグラフ
図2 シグモイド関数/tanh関数/ReLUの「導関数」(微分係数の関数)のグラフ



