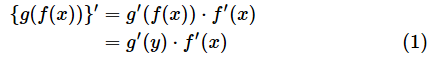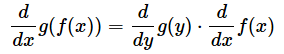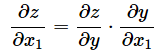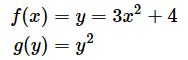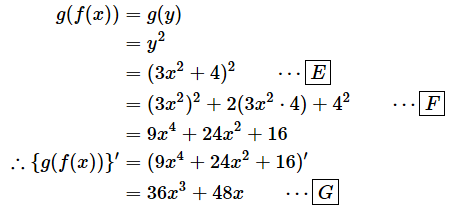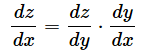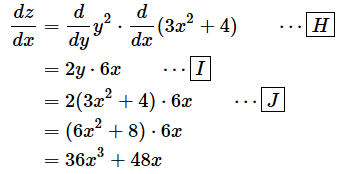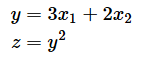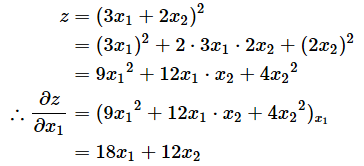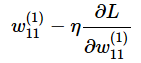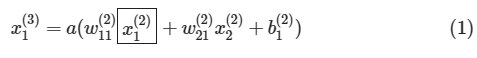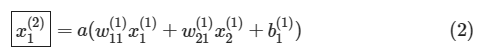�mAI�E�@�B�w�K�̐��w�n�������̔����i�A�����j�ƃj���[�����l�b�g���[�N�����̏����FAI�E�@�B�w�K�̐��w�����i2/2 �y�[�W�j
�ڕW�y����2�z�F �������̔���
�@�������̔����ɂ́A�ȉ��̌������g���܂��B
�@�ǂ̕ϐ��Ŕ������邩�m�ɂ��邽�߂ɁA�ȉ��̂悤�ɕ\�����Ƃ��ł��܂��B
�@����ɁAy��f(x)�Az��g(y)�Ƃ���ƁA���̌����́A�ȉ��̂悤�ɊȌ��ɕ\���܂��B
�@��������y�Ŕ����������̂�x�Ŕ����������̂̐ςɂȂ��Ă��܂��B�����̎��͕����ł͂���܂��A�������������ł��邩�̂悤�ɖł���Ƃ����킯�ł��B�i1�j�������Ӗ���������₷���ł��ˁB
�@���̎��́A���������X�ƂȂ����Ă���悤�Ɍ�����̂Łu�A�����ichain rule�j�v�ƌĂ�邱�Ƃ�����A�j���[�����l�b�g���[�N�ő������i�����Əo�͒l�̍���\�����j�̔������e�w�ɋt���ɂ����̂ڂ�Ȃ��玟�X�Ɠ`���邱�Ɓi���t�`�d�j��\���̂Ɏg���܂��B����ɂ���āA�d�݂�o�C�A�X�̒l�����Ă����Ƃ����킯�ł��B
�@�Δ����̏ꍇ�����l�ł��Bz��y�̊��ŁAy��x1,x2,...�̊��ł�����̂Ƃ��Az��x1�ŕΔ�������Ȃ�A�ȉ��̂悤�ɂȂ�܂��B
����y����2�z�F �������̔����i�A�����j
�@�������́A1�y�[�W�ڂŌ������@�Ŏ���W�J���Ă���������邱�Ƃ��ł��܂����A�������g���ƁA�X�e�b�v���Ĕ����ł��܂��B�j���[�����l�b�g���[�N�i���Ƀf�B�[�v���[�j���O�j�̑��������t�`�d����ꍇ�̂悤�ɁA���i�K�ɂ��킽�鍇�����̏ꍇ�A����������������S�ēW�J���Ă����������̂͌����I�ł͂���܂���B�������g���ăX�e�b�v����ƁA�r���̎����ȒP�ɂȂ�A�v�Z�����Ȃ胉�N�ɂȂ�܂��B
�@�������̔����̌����̈Ӗ����i1�j���Ɓi2�j���Ƃ��Ɍ��Ă����܂��傤�B
�@�i1�j���ł́Ag'(y)�̕�����y�ł̔����ɂȂ邱�Ƃɒ��ӂ��Ă��������B
�@�i2�j���̏��������ƁA�ǂ̕ϐ��Ŕ�������̂����悭������܂��ˁB���̎����悭����ƁA�ȉ��̐}9�̂悤�ɖƓ����悤�Ȍv�Z���ł��邱�Ƃ�������܂��B�t�Ɍ����ƁA���炩�̕ϐ����g���č������̔������E�ӂ̂悤�ȉ��i�K���̔����ɕό`�ł���Ƃ������Ƃł��B
�@�ł́A�ȒP�ȗ���g���āA�������̔����̌����̎g�����Ɋ���Ă����܂��傤�B��ɂ���Č����ߖ��ɂ��Ă����̂ŁA�l���Ȃ���ǂݐi�߂Ă����Ă��������B�����̓I�����W�F�̕������N���b�N�܂��̓^�b�v����Ε\���ł��܂��B�Ȃ��A����ł�������Ă���̂ŁA���ЎQ�Ƃ��Ă݂Ă��������B
�������̔����̗�1
����2�@�������̔����̗�1
�@2�̊����ȉ��̂悤�Ȃ��̂ł������Ƃ��܂��B
�@���̂Ƃ��A������g(f(x))��x�Ŕ������Ă݂܂��傤�B
�@�@{g(f(x))}' �� g'(f(x)) ⋅ f'(x)
�@�@�@�@�@�@�@�� g'(y) ⋅ f'(x) �@�@ ⋯
�mA�n
�@�@�@�@�@�@�@�� (�@y�@2)' ⋅ (3�@x�@2�{4)' �@�@ ⋯
�mB�n
�@�@�@�@�@�@�@�� �@2�@y ⋅ �@6�@x �@�@ ⋯
�mC�n
�@�@�@�@�@�@�@�� 2(3x2�{4) ⋅ �@6�@x �@�@ ⋯
�mD�n
�@�@�@�@�@�@�@�� (6x2�{8) ⋅ �@6�@x
�@�@�@�@�@�@�@�� 36x3�{48x
�mA�n ⋯
�����܂ł͍������̔����̌���
�mB�n ⋯
g(y)���@y�@2�Af(x)��3�@x�@2�{4��������
�mC�n ⋯
���������B�ς̑O�̍���y�Ŕ����A����x�Ŕ������Ă��邱�Ƃɒ��Ӂi��q�j
�mD�n ⋯
y��3x2�{4��������
�@�O�̂��߁A����W�J���Ă�������������ʂƌ���ׂĂ����܂��傤�B
�mE�n ⋯
y��3x2�{4��������
�mF�n ⋯
����W�J����
�mG�n ⋯
x�Ŕ�������
�@���R�̂��ƂȂ���A�����Ɠ�������v���Ă��܂��ˁB�����b��߂��܂����u'�v���g�������������ƁA�mB�n������������mC�n���ɂ���Ƃ��낪������Â炩�����Ǝv���܂��B�mB�n�����Čf���Ă����܂��B
�@���̏ꍇ�Ay2��y�Ŕ������A3x2�{4��x�Ŕ�������K�v������킯�ł����A���ꂪ�͂�����ƕ�����܂���ˁB�������A�ȉ��̏������ŕ\���ƁA���Ŕ������邩��������Ƃ͂���܂���B�u����v�ɂ����镔���ɏ����ꂽ�ϐ��i�Ⴆ��dz/dy�Ȃ�y�j�Ŕ�������Ƃ������Ƃ�������܂��B
�@���̂Ƃ��Ay��3x2�{4�Az��y2�Ȃ̂ŁA�ȉ��̂悤�ɂȂ�܂��B
�mH�n ⋯
�E�ӂ�z��y2�������Ay��3x2�{4��������
�mI�n ⋯
��������
�mj�n ⋯
y��3x2�{4��������
�������̔����̗�2�i�Δ����̏ꍇ�j
�@�Δ����̏ꍇ���v�Z���@�͓����ł��B����ɂ��Ă���̗�Ō��Ă����܂��傤�B�Ȃ��A�����������ł̉����p�ӂ��Ă���܂��B���ЎQ�Ƃ��Ă݂Ă��������B
����3�@�������̔����̗�2�i�Δ����̏ꍇ�j
�̂Ƃ��Az��x1�ŕΔ�������ƈȉ��̂悤�ɂȂ�܂��B
�@�@ ��z �@�@��z �@�@��y
�@�@�\�\ �� �\�\ ⋅ �\�\
�@�@ ��x1�@�@��y�@�@��x1
�@�@�@�@�@ �@ �݁@�@�@�@ �@�݁@
�@�@�@�@ �� �\�\ �@y�@2 ⋅ �\�\ (3�@x1�@ �{ 2�@x2�@) �@�@ ⋯
�mA�n
�@�@ �@�@�@�@��y �@�@ �@�@��x1
�@�@�@�@ �� 2y ⋅ �@3�@ �@�@ ⋯
�mB�n
�@�@�@�@ �� 2(3�@x1�@ �{ 2�@x2�@) ⋅ �@3�@ �@�@ ⋯
�mC�n
�@�@�@�@ �� (6x1 �{ 4x2) ⋅ �@3�@
�@�@�@�@ �� 18x1 �{ 12x2
�mA�n ⋯
�E�ӂ�z���@y�@2�������Ay��3�@x1�@�{2�@x2�@��������
�mB�n ⋯
��������
�mC�n ⋯
y��3�@x1�@ �{ 2�@x2�@��������
�@�O�̂��߁A�������̌v�Z���s���Ă���Δ������Č��ʂ���v���邱�Ƃ��m�F���Ă����܂��B
�@�͂��A�m���Ɉ�v���Ă��܂��ˁB�������̔����i�A�����j���A�����̊�{�I�Ȍv�Z���@���������Ă�����Ƃ͑���A�l�����Z�A�ׂ���Ƃ������P���Ȍv�Z�̐ςݏd�˂����łł��邱�Ƃ����������Ǝv���܂��B
�@�Ƃ���ŁA����̗�Ƃ��Ď�����XOR�̌v�Z���s���j���[�����l�b�g���[�N�ł́A�d�݂�\���ϐ���6���A�o�C�A�X��\���ϐ���3������܂��B���̂悤�ȒP���ȗ�ł��A���������d�݂�o�C�A�X�ŕΔ������A�t�`�d�̌v�Z���s������S�ď����Ƃ��܂�ɂ��ώG�ɂȂ��Ă��܂��܂��B�Ƃ肠�����A�����\���̗��}�ŕ\�������̂����f�ڂ��Ă����܂����A���̂܂܌v�Z���邱�Ƃ��l����ƋC�������Ȃ肻���ł��ˁB
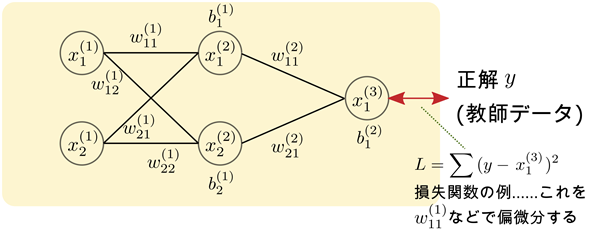 �}10�@�j���[�����l�b�g���[�N�Ƒ������̗�
�}10�@�j���[�����l�b�g���[�N�Ƒ������̗�XOR�����߂�j���[�����l�b�g���[�N�ƍ\���͓��������A�d�݂Ȃǂ��ŕ\���Ă���i�ϐ����������ς��Ă���j�B�ϐ����̉E����(1)(2)(3)�͉��w�ڂł��邩��\�����߂ɕt���Ă���B
�����ł́A�m�[�h��\���~�̒��ɏ����ꂽ�ϐ����͂��̃m�[�h������o����\�����̂Ƃ���B�Ⴆ�A�����̏�̃m�[�h��x(2)1�͑�2�w��1�Ԗڂ̃m�[�h����̏o�͂�\���B�o�C�A�X�̓Y�����ɂ��ẮA���Ԗڂ̃m�[�h�ւ������ɂ�����o�C�A�X�ł��邩��\���B�Ⴆ�A��������b(2)1�́A��1�w��2�Ԗڂ̃m�[�h�ɂ�����o�C�A�X��\���B�d�݂̓Y�����͉��Ԗڂ̕ϐ����牽�Ԗڂ̕ϐ��ɑ�����Ƃ��̏d�݂ł��邩��\���B�Ⴆ�Aw(2)21�ł���A2�Ԗڂ̕ϐ�����1�Ԗڂ̕ϐ��ɑ�����Ƃ��̏d�݂ł��邱�Ƃ�\���B
�@�������Ƃ͐����̒l�ƃj���[�����l�b�g���[�N�̏o�͂Ƃ̍��i�덷�j��\���悤�Ȋ��ł��B�Ⴆ�A�덷���悵���l�̑��a�i���a�덷�j�Ȃǂ��������Ƃ��Ďg���܂��B���������g���ďd�݂�o�C�A�X������ɂ́A��������Δ������A�w�K�����i�C�[�^�Ɠǂ݂܂��j���|���Ēl���X�V���܂��B�Ⴆ�A��������L�Ƃ��Aw(1)11���X�V����̂ł���A�ȉ��̂悤�ȍX�V�����l�����܂��i��7��̋L���ŊȒP�ɐ����������z�~���@�ł��j�B
�@�����ł́A���������������ɂȂ��Ă��邱�Ƃ��m�F���Ă����Ă������������ŏ\���ł��B�Ⴆ�A
�ƂȂ��Ă���A�����̂ڂ�ƁA
�ƂȂ��Ă��܂��B�g�ň͂���������������ł��邱�Ƃ�������܂��iXOR�����߂�j���[�����l�b�g���[�N�̗�ŋ�̓I�Ɍ������Ƃ��v���o���Ă��������j�B�����̍X�V����S�Ă̏d�݂ƃo�C�A�X�ɂ��Čv�Z����K�v������킯�ł��B
�@�����̎��������ƊȒP�ɕ\�����@������A�d�݂�o�C�A�X����C�ɋ��߂邱�Ƃ��ł���̂ł����A�����_�ł͂܂��������Ă��܂���B���������킯�ŁA����́u�͂��߂̈���v�Ƃ������Ƃō������̕Δ����̕��@���m�F����Ƃ���܂łɂƂǂ߂Ă������Ƃɂ��܂��B�c�c�ŁA���́A���̓���Ƃ����̂��x�N�g����s��A�܂���`�㐔�ł��B����͐��`�㐔���w��ł����A���������������𐰂炵�Ă��������Ǝv���܂��B
����́c�c
�@����͐��`�㐔�̊�{�Ƃ��āA�܂��̓x�N�g���̍l�����Ɗ�{�I�Ȍv�Z�i�a�E���E���ρE�x�N�g���̒����j�ɂ��Č��Ă����܂��B�x�N�g�����g����悤�ɂȂ�Ƒ����̒l��ϐ���������1�̕����ŕ\�����Ƃ��ł��܂��B�܂��A�x�N�g���́u�ގ��x�v�����߂�v�Z�Ȃǂւ̉��p���ł��܂��B
�X�V�����i2025�N2��19���j
�}10�̑������̒�`����� w �̓Y�����Ɉꕔ��肪���������߁A�}10�������ւ��A�⑫������NjL���A�u�����ł́A���������������ɂȂ��Ă���c�c�v�Ŏn�܂�1�����C�����܂����B��肪����܂������Ƃ����l�т��A�����������܂��B
Copyright© Digital Advantage Corp. All Rights Reserved.
�A�C�e�B���f�B�A����̂��m�点
��IT eBook