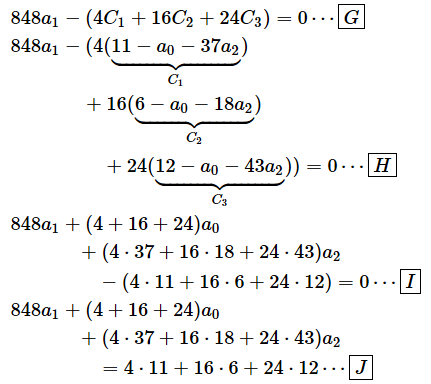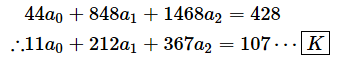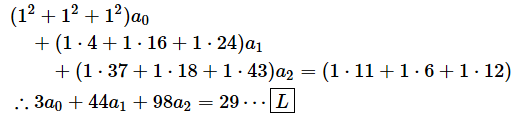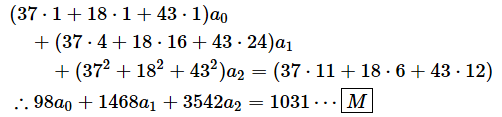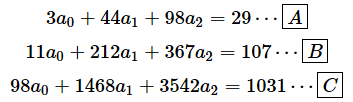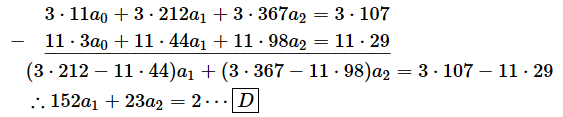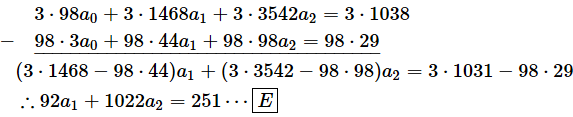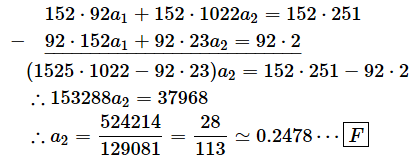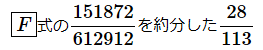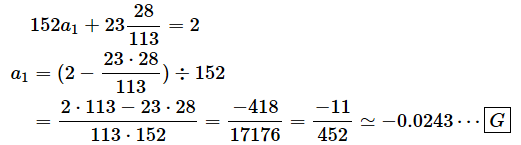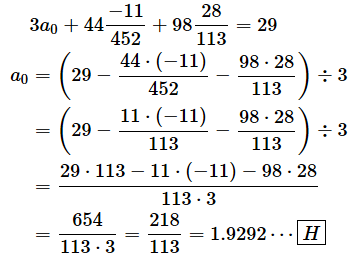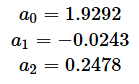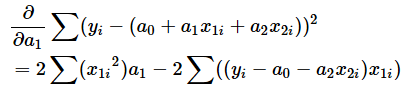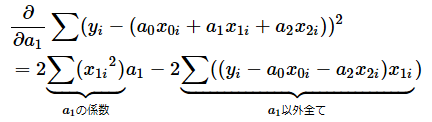［AI・機械学習の数学］偏微分を応用して、重回帰分析の基本を理解する：AI・機械学習の数学入門（2/2 ページ）

[羽山博，著]

残差二乗和を偏微分する

　では、いよいよ、Qをa₁で偏微分してみましょう。ここも確認しながら進めたいので穴埋めにしておきます。オレンジ色の部分をクリックするかタップすると答えが表示されます。また動画での解説も用意してあります。ぜひ視聴してみてください。

動画2　残差平方和の微分

∂Q
―― ＝ (848a₁² − 　2 (4C₁ ＋ 16C₂ ＋ 24C₃)　 a₁ ＋ 　ΣC_i²　)_a1
∂a₁　　　　　　　 　定数　　　　　　　　　定数項　として扱う　
　　 ＝ 　2　 ・ 848a₁ − 2(4C₁ ＋ 16C₂ ＋ 24C₃) …… ［F］

［F］ ⋯ a₁で偏微分した。定数項は消える

　［F］式は二次式で、a₁の二乗の係数は正なので、下に凸な関数ですね。従って、偏微分した［F］式を0と置けば残差二乗和の式Qを最小にするa₁の値が求められるはずです。

　両辺を2で割ってから、C_iを元に戻すと以下のようになります。かっこを外すときに、かっこの前にマイナスがあることに注意してください。−(−a＋b)＝a−bのように、かっこの中のマイナスはプラスに、プラスはマイナスになります。

［G］ ⋯ 両辺を2で割った。さらに両辺を4で割ることもできるが、後で仕組みを見たいので、この段階ではこのままにしておく
［H］ ⋯ C_iを元に戻した
［I］ ⋯ a₀とa₂で整理し、その順に項を並べ替えた
［J］ ⋯ 定数項を右辺に移項した

　あとは［J］式の数字を計算するだけです。結局、以下のような式が得られます。∴という記号は「ゆえに」「従って」という意味です。

［K］ ⋯ a₀から順に並べて、係数と定数項を計算した。両辺を4で割った。

　はい、だいぶ簡単になりましたね。残差二乗和を最小にするようなa₁の値は［K］式を解けば求められるということです。ところが、［K］式にはa₀やa₂という未知数が含まれていますね。なので、これだけでは答えは求められません。そこで、a₀やa₂についても同じように偏微分して0と置く必要があります。……というのはまた大変ですよね。そこで、ちょっとズルをします。［K］式の前の段階の［J］式で係数と定数項の特徴について、順を追って見てみましょう。

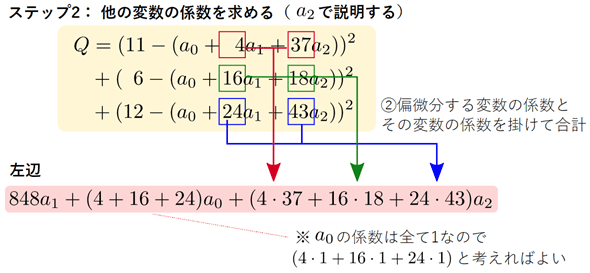
　図3（a₁で微分する例）を見ると、以下のようになっていることが分かります。

図3　係数の特徴（偏微分する変数）

　ステップ1： 偏微分する変数の係数は、（1）元の式の係数の二乗和とする（図3）。例えば、a₁で偏微分するなら、元の式のa₁の係数である4、16、24の二乗和が、偏微分した後のa₁の係数になる。

図4　係数の特徴（他の変数）

　ステップ2： それ以外の係数は、（2）偏微分する変数の係数と元の式の係数を掛けたものの合計とする（図4）。例えば、a₂の係数は、元の式のa₁の係数である4、16、24と、元の式のa₂の係数である37、18、43をそれぞれ掛けたものの合計になる。

図5　係数の特徴（定数項）

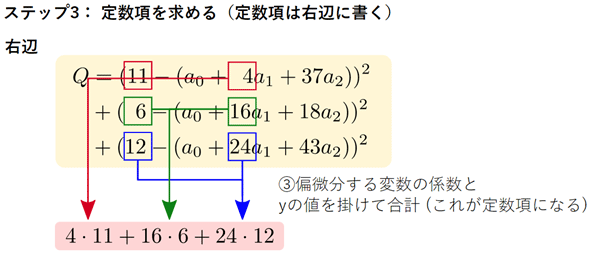
　ステップ3： 定数項もステップ2と同じ考え方で求める。（3）偏微分する変数の係数とy（観測値）の値を掛けたものの合計とする。ただし、定数項は右辺に書く（図5）。例えば、元の式のa₁の係数である4、16、24と、元の式のyの値(家賃)である11、6、12をそれぞれ掛けたものの合計になる。

　これらのルールをa₀やa₁に対して適用すれば、それぞれの式が立てられそうですね（実際に偏微分して0と置くという計算をすると、これらの式が得られます）。a₀について偏微分して0と置いたときの式は以下の通りです。

［L］ ⋯ a₀で偏微分して0と置いた場合。a₀の係数は全て1なので二乗和は3

　a₂について偏微分して0と置いた場合は以下のような式になります。

［M］ ⋯ a₂で偏微分して0と置いた場合。a₁の係数は37、18、43だったので、それらを各項の係数に掛ける。37、18、43の二乗和は3542

　以上で、3つの式が出そろいました。これらの式は連立方程式になっていますね。この3つの式が同時に成り立つのであれば、残差二乗和（Q）の式が最小になるといえます。そのときのa₀、a₁、a₂の値を求めるために、この連立方程式を解くことにしましょう。なお、機械学習では、偏微分して0と置いて連立方程式を立て、それを解くという方法を採らずに、偏微分係数を使って少しずつ値を変えていく方法を使います。

　そういうわけで、連立方程式の解き方にあまり興味がないという人は、概略だけですが、機械学習での係数の求め方も示しておいたので、そこまで読み飛ばしてもらっても結構です*3。

*3　連立方程式は、Wolfram Alphaなどのサイトを使って解くこともできます。

連立方程式を解く

　偏微分して0と置いた式をもう一度まとめて掲載しておきます。あまりに長い道のりで、使えるアルファベットがなくなってきたので、式の番号を［A］から振り直しますね。

　［A］式は［L］式を再掲したもの、［B］式は［K］式を再掲したもの、［C］式は［M］式を再掲したものです。これらの連立方程式を解けば、a0、a1、a2が求められますね。

　まず、［A］式を使って［B］式と［C］式からa₀を消去しましょう。［B］式を3倍したものから［A］式を11倍したものを引けば［B］式からa₀が消せます。

　同様に、［C］式を3倍したものから［A］式を98倍したものを引けば［C］式からa₀が消せます。

　次は、［D］式を使って［E］式からa₁を消します。［E］式を152倍したものから［D］式を92倍したものを引けば、a₁が消せます

　a₂の値が求められました。0.2478です。

　次に、［D］式にa₂の値を代入して、a₁の値を求めます。a₂の値は、

を使うのがいいでしょう（0.2478は小数点以下を四捨五入した近似値なので）。

　a₁の値も求められました。-0.0243ですね。最後に、a₁とa₂を［A］式に代入してa₀を求めます。

　ようやく答えにたどり着きました。［F］［G］［H］より、

となり、回帰式は、

となりました。これは最初に見た結果とちゃんと一致していますね。この式を使えば、さまざまな「築年数（x₁）」と「面積（x₂）」から「家賃（y）」が予測できるというわけです。

　最小二乗法による重回帰分析の手順は、

1. 観測値と予測値の差（残差）の二乗和を求める
2. 各係数を変数と見なして偏微分する
3. それによって導き出された連立方程式を解いて各係数を求める

というものでした。しかし、連立方程式は変数が多くなると、コンピュータを使って解くための計算量が増えるので、かなり時間がかかります。

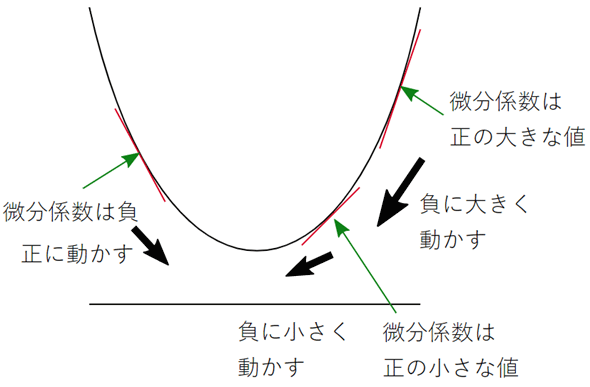
　そこで、機械学習では、ここで見たように連立方程式を解いて答えを導き出すのではなく、偏微分した式に適当な値を入れて、微分係数の符号を見るという方法を使うのが一般的です。微分係数の符号が正であれば、最小値はもっと左にあるはずです。つまり、もう少し小さなx_iを与えてあげれば最小値に近づきます。逆に、微分係数の符号が負であれば、最小値はもっと右にあるはずです。この場合は、もう少し大きなx_iを与えてあげれば最小値に近づきます。つまり、微分係数の符号と反対の方向に動かせばいい、というわけです（図6）。

図6　最小値を見つける

　図の右側を見てください。最小値から遠く離れていると、微分係数は正の大きな値になるので、それを引いてあげればぐっと最小値に近づきますね。最小値に近いと、微分係数も小さい値なので、それを引いてあげると少しずつ最小値に近づきます。図の左側は、微分係数が負の場合です。その場合は微分係数を引く（負の値を引くので、足すことに絶対値を足すことになります）と最小値に近づきます。

　ただし、微分係数をそのまま足したり引いたりするのではなく、微分係数に小さな値を掛けて使います。例えば、勾配降下法などでは、直前のx_iから「適当に選んだ小さな値×微分係数」を引くという計算を繰り返します。そして、値がほとんど変化しなくなったとき（＝収束したとき）のa_iを求めるというわけです。この「適当に選んだ小さな値」のことを「学習率」などと呼び、η（イータと読みます）などの文字を使って表します。学習率の値を大きく設定すると、正と負の間を行ったり来たりして収束しなくなることがあるので注意が必要です。また、学習率の値が小さすぎると収束に時間がかかります。

まとめと補足

　最後にまとめと補足です。

残差二乗和の偏微分（一般的な場合）

　ここまでは、具体的な数値を使って偏微分を利用した回帰分析の例を見てきました。これを一般化するとどうなるかということですが、実は、前回の練習問題の3番がその計算の一部になっています。そういうわけで、3番を後回しにした人もいったん戻ってぜひチャレンジしてみてください。答えは、以下の通りでした。

　回帰式が、

のとき、いくつかのデータを基に求めた残差二乗和の式は以下のようになります。y_iやx_1iなどがそれぞれのデータを表します*4。

*4　変数を区別するための添字と、個々のデータを区別するための添字が紛らわしくなるので、個々のデータを区別するための添字を右肩にかっこ書きで示すこともよくあります。上の例であれば、以下のようになります。

　これをa₁で偏微分すると以下のようになります。

　a₀やa₂で偏微分する場合でも同じですし、回帰式の変数がもっと増えても同じです。なお、a₀をa₀x₀と表し、x₀が常に1であると考えれば、以下のように書けます（形式をそろえただけです）。

　つまり、すでに見てきた通り、

1. 偏微分する変数（例えばa₁）については、係数の二乗和を係数とする
2. それ以外の項（例えばy_iやa₀、a₂）については、偏微分する変数の係数（例えばx_1i）とそれぞれの変数の係数（例えばy_iそのものやx_0i、x_2i）を掛けたものの合計を係数とする

というわけです。

　さらに、回帰式の変数がx₀からx_mまであるものとし、それぞれのデータの個数がn個(1〜nまで)であるとき、残差二乗和の式をa_kについて偏微分する場合の一般的な式を書くと以下のようになります。ただ、以下の式は、全てを一般化し、しかもできるだけ簡潔に書いたものなので、ぱっと見て「理解できた」というわけにはいかないかもしれません。あくまで参考用のものなので、今はあまり気にしなくても大丈夫です。具体的なイメージとして、不動産データの回帰分析の方法が理解できていれば十分です。

　回帰式が、

のとき、残差二乗和は以下のようになります。

［A］ ⋯ 残差二乗和の式の中の、a₀x_0i〜a_mx_miの和をΣで書いた

　これをa_kで偏微分すると以下のようになります（式の変形は前回の練習問題の3番と同じなので、結果だけを示しています）。

　ちょっとやりすぎな感じもしますが、これが一般的な形式になるというわけです。*5。

*5　ごく単純な計算であれば、具体的な数値を使った方がイメージをつかみやすいのですが、変数が増えてくると、むしろ文字や記号を使った方が式の意味や計算の手順がよく分かりますし、計算を間違うことも少なくなりますね。

次回は……

　というわけで、今回は最小二乗法による重回帰分析に偏微分を利用するお話を見てきました。偏微分は回帰分析だけでなくニューラルネットワークなどでも使われるので、機械学習やディープラーニングには必須の数学です。

　といっても、偏微分の計算そのものは簡単でしたね。難しく思えるのは係数や変数、重みなどにさまざまな文字を使ったり、Σなどを使って一般的に式を記述したりすることがあるからです。そういうときには、できるだけ簡単な例で具体的な数値を使って試しに計算してみると少しずつ意味が分かってくると思います。

　次回は、微分の積の公式や合成関数の微分（連鎖律）などについて見ていきたいと思います。

「AI・機械学習の数学入門」