AIモデル学習の評価時／オペレーション時に発生するバイアスリスク、どう対処する？：エンジニアが知っておくべきAI倫理（3）

正しくAIを作り、活用するために必要な「AI倫理」について、エンジニアが知っておくべき事項を解説する本連載。第3回は、AIモデル学習の評価時、オペレーション時のバイアスリスクへの対処法について。

[保科 学世, 張 瀚天，アクセンチュア]

　前回はデータのバイアスリスクへの対処法を、具体例を交えて解説した。今回は、AIモデル学習の評価時、オペレーション時のバイアスリスクへの対処法について解説する。考え方や手法、ツールがAI開発の一助になれば幸いだ。

AIモデルの不透明さ、不可解さをどう解決するか

　AIモデルにおいて、「精度は高いがなぜその出力がなされているか理解しがたい」といった問題が発生し得る。特にディープラーニングなどのAIモデルにおいて、モデルの入出力関係が解釈しづらく、ブラックボックスとなり、AIが誤った基準で判断をしているかを解釈できないケースが存在する。例えば、既存の知見と異なる判断基準が学習されているケースや、人種、民族、性別、年齢、信仰などの公平性観点から差を生むべきではない、いわゆる「センシティブ属性」がAIの判断基準に使われてしまっているというケースである。そうした問題を検知し解消するため、モデルの解釈性を向上させることが重要だ。

　モデルの解釈性を向上する方法は大きく分けて2種類ある。「AIモデル自体の解釈性を向上させる方法」と「学習したモデルを解釈する方法」だ。

1．AIモデル自体の解釈性を向上させる方法

• A）条件分岐構造を持つモデル

　モデル自体の解釈性を向上させるには、条件分岐構造を持つモデルが有効である場合が多い。条件分岐構造を持つモデルの代表例は決定木である。

　前述の通り、解釈性の高いモデルを構築することでAIモデルが誤った判断をしているかを解釈できる。ここで、決定木の簡単な活用例を紹介する。

図1：決定木によるStatlog（German Credit Data）学習例（dtreevizによる可視化）（作成：アクセンチュア

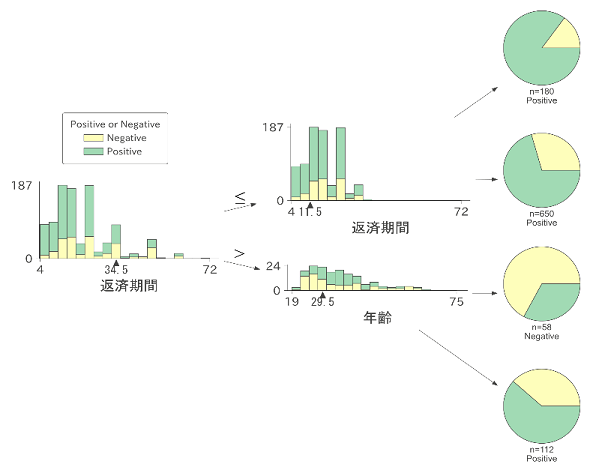
　図1は1970年代ドイツの金融機関における融資リスクを、融資返済期間や年齢といった特徴（今回は例示のため、あえて年齢などセンシティブ属性をそのまま変数に加えている）から予測する決定木を構築した例である。

　決定木は分岐ごとに条件がANDで足される構造となっている。上図を読み解くと、4つのパターンが学習されている。返済期間が11.5カ月よりも短い場合に最も低リスク（Positive）であり、11.5カ月超34.5カ月以下の場合も低リスクと予測されている。また、返済期間が34.5カ月以上と長期で、年齢が若い場合（29.5歳以下）に特に高リスク（Negative）となっており、年齢がそれよりも高い場合には低リスクとなる。このように、決定木はデータから解釈可能な条件分岐構造を可視化できる。

　一方で、モデル解釈した後に、次のステップとして考慮すべきことがある。それは、「年齢が若いと融資リスクが高い」とするモデル判断が妥当か否かである。

　米国の金融サービスの公平性を担保するために作られた消費者信用機会均等法（ECOA）においては、「年齢」はセンシティブ属性と定められているため、年齢が判断基準に含まれるモデルは公平性を欠いたモデルといえる。

　そのため年齢の影響を除いたモデルを構築する必要がある。しかし、ここで年齢を除いてモデルを構築するだけでは、年齢に関した暗黙的な関連がモデル内部に含まれ、公平でないモデルが構築される可能性がある。そのため、前回記事で解説した公平性を配慮したAIモデル構築技術の適用が必要になるのである。

　上記例のように、決定木など解釈性が高いモデルは、モデル内部でどのように判断されているかを可視化でき、モデル判断が妥当かを考察することが可能になる。そして、その結果によってはバイアスを取り除く、といった改善プロセスを取ることができるため、よりバイアスリスクを抑えたAIモデルが構築可能になるのである。

　また、今回の例においては、そもそも融資リスクを予測するようなモデルを構築すべきか、という根本的な問題がある。第1回記事で解説した、AI設計時のバイアスリスクである「コンセプトの欠陥」や「確証バイアス」などを慎重に考慮しなければならない。

　その他にも、条件分岐構造を持つモデルとして「RuleFit」がある。RuleFitでは、勾配ブースティングなど、複数の木で構成されるモデルで学習した条件分岐構造を用いる。学習した条件分岐構造を特徴量として表現し、線形モデルとして学習することで、各条件分岐の重要度を示すことができる手法である。

　この節で紹介した決定木は機械学習ライブラリ「scikit-learn」で公開されている。またRuleFitや可視化ツールである「dtreeviz」についてもオープンソース実装が公開されている。

• B）加法的な構造を持つモデル

　過度に複雑なモデルでない場合には、加法的なモデルでも解釈性を向上させることができる。加法的なモデルは、

と表される。特徴量ごとに目的変数(y)へ関係が表現されているため、各特徴量の目的変数への影響を理解しやすいモデルである。

　加法的なモデルの代表例として、「線形回帰モデル」が挙げられる。線形回帰モデルは、目的変数を特徴量の重み付け線形和（fが重み係数）として表現するため、各変数の重みにより目的変数への影響度を把握できる。また、目的変数に対して適切な非線形変換（リンク関数, g）をする一般化線形モデル（Generalized Linear Models）が存在する。

　その他にも、より柔軟なモデルとして、各特徴量の関係(f)についても、スプライン曲線など非線形関数を用いる「一般化加法モデル」（GAM、Generalized Additive Model）がある。

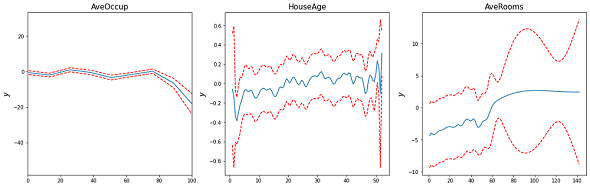
　図2がGAMの学習例だ。これは、カリフォルニアにおける各地区の家の値段の中央値を予測するモデルを、平均住宅占有率（AveOccup）や築年数の中央値（HouseAge）、平均部屋数（AveRooms）などの特徴量からGAMにより構築し、それぞれの影響度(f)を可視化したものだ。青字が予測値であり、赤字は95％信頼区間である。

　結果を見ると、AveOccupが高くなるほど目的変数の値が下がり、HouseAge、AveRoomsが高くなるほど信頼区間は広いもののおおむね目的変数が上昇する傾向が学習されている。

図2：GAMによる変数影響の可視化例（pyGAM）（作成：アクセンチュア）

　このように、加法的モデルでは各項の影響を可視化できる。GAMやGLMに関して、pyGAMにて実装が公開されている。

• C）関係性制約付きモデル

　特徴量の目的変数へ与える影響が分かっている場合には、その知見を反映させたモデルを構築することで解釈性を向上させることができる。

　例えば、販売価格が下がったら需要が増えるといった「単調性」や、年齢が上がるほど収入は上がるが一定の年齢を過ぎると低減するといった「凹凸性」などの関係だ。

　単調性制約に関しては「XGBoost」や「LightGBM」などの代表的な機械学習ライブラリでもサポートしている。例えば、LightGBMについては引数「monotone_constraints」に対して、各変数に単調性制約を課すかどうかを指定できる。前節で紹介したpyGAMも、単調性や凸（convex）と凹（concave）を制約として関係性(f)を学習できる。

　関係性制約を課して学習させた例を下図に示す。図3の左はlog関数で表現される目的変数に対して、凹性制約付きGAM、単調性制約付きLightGBMの学習例だ。右の図は目的変数に対して2変数がそれぞれ凹凸関係の場合に制約付きGAMで学習した例である。

図3：（左）凹性、単調性制約付きの学習例（右）凹凸制約を加えたGAMの学習例作成（作成：アクセンチュア）

　このように制約を加えることで、データに対する知見に合うモデルを構築可能だ。また、凸性制約付きモデルは、凸最適化によって取り扱いやすい関数が学習されるため、最適化問題との親和性も高い。

　ただし知見を入れることができるということの裏返しとして、その知見を重視してしまうような「確証バイアス」のリスクを意識しなければならない。

2．学習したモデルを解釈する方法

• A）モデル内部で寄与する特徴量の理解

　予測モデルを解釈するには、AIモデル内でどの特徴量がどの程度寄与しているかを読み解く必要がある。変数の重要度を算出する手法として、「Permutation Feature Importance」が挙げられる。

　これは、AIモデル学習後に各特徴量のデータをシャッフルして予測を実施し、「予測誤差が増加する度合い」をその特徴量の重要度とするシンプルな手法である。シャッフルしているのに予測誤差が増えない変数は重要度が低く、誤差が増える特徴量は重要度が高いと考えられる。

　また、特徴量値とモデル予測値の関係を可視化する手法として、「Partial Dependence Plot」（PDP）が挙げられる。PDPは各特徴量値を単一の値で固定した場合の予測値の平均値をプロットしたものであり、各特徴量の値の大小で、どのように予測値が変化しているかを可視化できる（図4）。

図4：PDPの例（出典：https://scikit-learn.org/stable/_images/sphx_glr_plot_partial_dependence_003.png）

　例えば、図4の左にあるAveOccupについては、値が上昇するにつれて予測値が減少し、一方でHouseAgeが上昇すると予測値が増加する傾向が見られる。

　PDPによって可視化するプロットは、GAMによる可視化（図2）と近い。PDPはモデル非依存という利点を持つが、特徴量の分布を無視して値を固定化させた場合の予測値を算出するため、現実にはありえないデータ分布となる可能性があり注意が必要だ。

　上記で紹介した、Permutation Feature ImportanceやPDPは、scikit-learnに実装が公開されている。

• B）SHAP

　モデル解釈において代表的な手法が「SHAP」だ。勾配ブースティング木やニューラルネットワーク（の一部）など複雑なモデルに対して、「各サンプルにおいての各特徴量の寄与度」を算出できる。

　図5は1サンプルに対するSHAPの例で、縦軸は特徴量、横軸は寄与度を表している。例えば、このサンプルに対しては特徴量13の値が4.98であることが予測を+5.79と押し上げているが、一方で特徴量6の値が6.575ということが予測値を-2.17に押し下げていると解釈する。

図5：SHAPの推定例（作成：アクセンチュア）

　このように各サンプルに対して各特徴量の寄与度を算出できる。

　また、SHAPによる寄与度は数多くの望ましい性質を持つ。例えば、寄与度（上例では+5.79や-2.17など）の合計は、そのサンプルのAIモデル予測値と一致する。つまり、SHAPによる寄与度は予測値の分解として解釈できる。

　また、全サンプルに対して変数値と寄与度をプロットすることでPDPのように特徴量値と予測値の関係を把握でき、各特徴量に対しての寄与度の絶対値の平均などを変数重要度として解釈できる。実装は「shap」ライブラリとして公開されている。

---

　ここまでで、モデルの解釈性向上の方法を解説した。取り上げたもの以外にも、既知の特徴量間の関係を反映した予測モデルを構築できるベイジアンネットや、「各サンプル」のAIモデルにおける重要度を算出する影響関数（influence function）などが存在する。より詳細には後述の参考文献を見ていただきたい。

モデルバイアスへの対処

　データに潜む社会的偏見などのバイアスがモデルによって増幅されてしまうことがあるため、前回紹介したように公平性に配慮したAIによりリスクに対処する必要がある。

　さらに、目的変数のデータの質が担保できず、モデルの学習や評価が難しい場面がある。特に大規模データセットで、複数の担当者がラベルを付与する場合などは、ラベル（目的変数）の質を担保することが難しい。その場合に、目的変数にラベルの振り間違いなどのノイズが存在する前提で学習する手法がある。

　その手法の一つが「Label Smoothing」だ。通常、クラス分類問題の目的変数は、各クラスに所属する場合1として、所属しない場合0の2値で表現するが、Label Smoothingではその値をいわば「にじませる」のだ。0か1か、と明確に2値に分けるのではなく、例えば、1とラベル付けされているものを0.9とし、0を0.1とするといったように、多少の振れ幅をもたせることで与えられた信頼できないラベルを過度に学習しないような頑健なモデルを構築できる。

　その他に、「Confident Learning」という手法もある。Confident Learningでは学習データの中で信頼できないラベルのサンプルを判別、除去した上で、再学習することで、より信用できるモデルを構築できる。

　Confident LearningをMNIST（手書き数字分類）データセットに対して実施した例が図6である。赤枠で囲われているのがラベルの振り間違いが起きていると提示されたデータであり、与えられたラベルがgiven、予測されているラベルがguessである。

　例えば左上の画像の場合、ラベルは4であるが実際の値は7であり、ラベルのミスが発生している。

図6：MNISTにおいてConfident Learningを実行した例（出典：https://github.com/cleanlab/cleanlab）

　Confident Learningはモデル非依存手法だ。任意の分類モデルで利用でき、実装が「cleanlab」というライブラリとして公開されている。

AIモデル運用でのリスク、オペレーションバイアスとは

　せっかく訓練させたAIモデルの精度や品質も、運用の段階で劣化してしまうリスクがある（オペレーションバイアス）モデルが学習したデータ分布や目的変数への関係式が、推論時、運用時に変化することが主要要因だ。例えば、気候変動で地球の気候そのもののパターンが変化していて、気温データに関する前提条件が変わるケースなど、数多くの事象が考えられる。

　その中でも、特徴量データの分布が変わってしまう場合は共変量シフト、目的変数の分布が変わってしまう場合はターゲットシフト、特徴量データと目的変数の条件付確率が変わってしまう場合はデータセットシフト（概念ドリフト）などがある。これらのシフトに対応するには、大きく分けて2つの方法がある。

　1つ目の対処法は、再学習だ。定期的に、推論したときと異なる現象が発生していると考えられる過去データを捨てて再学習する、もしくは新しいデータに対して大きな重みを付けて再学習するのだ。

　あるいは、シフトを検知したタイミングで再学習を実施する方法もある。シフト検知は、例えば特徴量と目的変数の基礎統計量をロギングし、その標準偏差などでシフト発生を判断する。その他に、学習データと推論（に近い）データ分布について違いがないかを仮説検定する方法がある。1変数に対しては「コルモゴロフ-スミルノフ検定」、多次元の場合は「Maximum Mean Discrepancy」（MMD）などにより仮説検定し、分布の違い、つまりシフトを検知する。

　2つ目の対処法としては、シフトによる分布の違いなどを考慮した新たなAIモデルの構築だ。例として、共変量シフトに対しての対処法を解説する。

　共変量シフトが発生するときは特徴量の分布が変化しているため、「学習用」の特徴量データと、「推論用」の特徴量データを分類するAIモデルを構築できる。

　そうして構築したモデルを用いた各サンプルに対して、推論用データである確率と学習用データである確率の比を算出する。その確率比を損失関数に対して重み付けて予測モデルを学習することで、「推論用データの特徴量分布」に対して推定したモデル構築ができる。

　これはサンプリングバイアスの緩和策として紹介した手法と近い考えであり、実装自体も重みを変えるだけで同様に可能である。

　また、増分学習（Incremental Learning）やオンライン学習（Online Learning）モデルを用いて最新データの分布に適用しながらモデルを更新していく方法も有用だ。

　MMDなどの仮説検定は「Torchdrift」、増分学習やオンライン学習のアルゴリズムについてはscikit-learnや「river」「scikit-multiflow」などでPython実装が公開されているため参考にしていただきたい。

　今回までで、各AI開発プロセスにおけるバイアスリスクと、それを緩和する具体的な技術手法について解説した。AIの社会実装が進んでいく中で、今後はより倫理的側面への配慮が求められるであろう。次回は、日本を取り巻く世界のAI倫理状況について解説する。

筆者紹介

保科 学世（ほしな がくせ）

アクセンチュア ビジネス コンサルティング本部 AIグループ日本統括 兼 アクセンチュア・イノベーション・ハブ東京共同統括 マネジング・ディレクター 理学博士。

アナリティクス、AI部門の日本統括として、AI HubプラットフォームやAI Poweredサービスなどの各種開発を手掛けるとともに、アナリティクスやAI技術を活用した業務改革を数多く実現。『責任あるAI』（東洋経済新報社）はじめ著書多数。

張 瀚天（ちょう かんてん）

アクセンチュア ビジネス コンサルティング本部 コンサルタント

筑波大学大学院卒業後に、アクセンチュア入社。ヘルスケアや通信など複数業界でのアナリティクス適用、AIモデル構築や運用による業務改革を支援。

特集：AIを使う人、作る人に知ってほしい　「AI倫理」との付き合い方

システムやサービスにAI（人工知能）を活用することが珍しくなくなった昨今、AIが引き起こす倫理的な問題もまた身近なものとなった。すでに欧米諸国ではAI倫理に関する法整備も進んでおり、日本国内にもその影響が及ぶことは想像に難くない。本特集ではそんなAI倫理について「AI倫理とはどういうものなのか」といった初歩的なテーマから「AI倫理に関してエンジニアは何を知っておくべきなのか」「AI倫理の観点から見たAI開発プロセスにおけるリスクとその対処法とは何か」といった実践的なテーマまで、深堀りして解説する。

特集：AIを使う人、作る人に知ってほしい　「AI倫理」との付き合い方

参考文献

UCI Statlog（German Credit Data）Data Set

• AIモデルの不透明さ、不可解さ

Interpretable Machine Learning（原文、日本語訳）

RuleFit

pyGAM

causalnex

• 測定バイアス、モデルバイアスへの対処

Confident Learning（論文、実装：cleanlab）

• オペレーションバイアス

非定常環境下での学習：共変量シフト適応，クラスバランス変化適応，変化検知／杉山将、山田誠、ドゥ・プレシ マーティヌス・クリストフェル、リウ ソン／日本統計学会誌、vol.44、no.1、pp.113-136／2014

Torchdrift

River

scikit-multiflow