JSダイバージェンス（Jensen-Shannon Divergence）とは？：AI・機械学習の用語辞典

2つ（以上）の確率分布間のズレを測る指標で、KLダイバージェンスをベースに「対称化」し、「値の範囲が0以上～1以下に収まる」ようにしたもの。複数の分布間の類似度を測ることができ、主に自然言語処理や生成モデルの評価、クラスタリングなどで利用されている。

» 2025年09月03日 05時00分公開

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

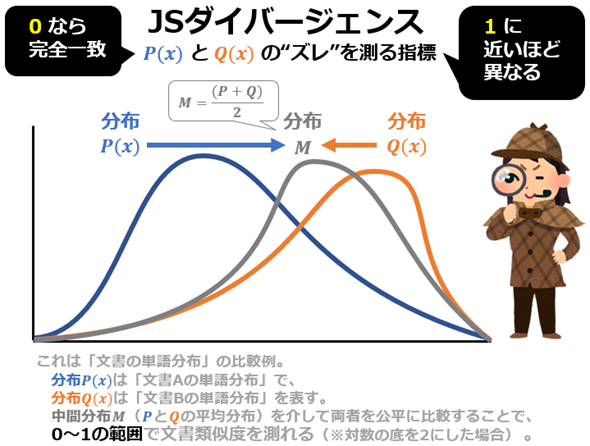
　情報理論／統計学／機械学習におけるJSダイバージェンス（Jensen-Shannon Divergence）とは、2つ（以上）の確率分布間の“ズレ”を測る指標である。KLダイバージェンスを基に改良された指標で、KLの欠点であった「非対称性」と「値が無限大になる可能性」を解消している。例えばPとQという2つの分布があるとき、それぞれを「中間分布M」と比較することで、両者の違いをKLダイバージェンスのように一方向だけでなく、両方向から公平に測り（＝対称性）、しかも結果が（基本的に）0以上～1以下の範囲に収まる有限の値として評価できる（図1）。

図1　JSダイバージェンスのイメージ

　JSダイバージェンスの値は、常に0以上の値を取り、0なら「完全に一致する分布」、1なら「完全に分離した分布」を意味する（※対数の底を2にした場合。この理由については後述する）。

　この値は、既に説明した通り「対称的」、つまりPとQの順序を入れ替えても同じ結果になる。よって、KLダイバージェンスのように「真の分布」と「近似分布」に分布の役割を固定する必要はない。数学的に表すと、D_JS(P‖Q) ＝ D_JS(Q‖P)である。さらに、D_JSの平方根を取ったもの（＝ジェンセン・シャノン距離：Jensen–Shannon Distance）は、数学的に“距離”の性質を満たす。

用途

　JSダイバージェンスは「確率分布同士の類似度（あるいは距離）」を評価できるため、以下のような用途で広く使われている。

自然言語処理： 文書の出現単語分布同士を比較し、類似文書検索や分類に利用。
生成モデルの評価： GAN（敵対的生成ネットワーク）において、生成データと実データの分布の違いを測る。
クラスタリング： データ集合を分布で表し、それらの類似度を測って分類する。
情報検索： 検索結果の分布とユーザー意図の分布のズレを比較。

JSダイバージェンスが使われる確率分布

　KLダイバージェンスと同じ確率分布（ベルヌーイ分布、二項分布、正規分布など）に適用できる。詳しくはKLダイバージェンスの記事を参照してほしい。

定義と数式

　JSダイバージェンスは、数式では以下のように定義される。

　まず、2つの確率分布PとQに対して、その「混合分布（直感的に表現すると平均分布、中間分布）」Mを以下のように定義する。

　このとき、JSダイバージェンスはKLダイバージェンスを用いて次のように表される。

D_JS …… 「JSダイバージェンス」を指す。
D_KL …… 「KLダイバージェンス」を指す。その数式はKLダイバージェンスの記事を参照。ただしJSダイバージェンスでは、KLダイバージェンスの数式内の対数の底を2とするのが一般的。
‖ …… 「比較対象の区切り」を表す。例えば(P ‖ Q)は「Pを基準にQとの違いを測ること」を意味する。

　このように、PとQそれぞれを混合分布Mと比較し、その平均を取ることで「対称性」が得られ、値が有限に収まる。

　さらに、KLダイバージェンスの数式にある対数部分を「自然対数（＝ネイピア数eを底とする対数）」ではなく、底を2とする対数に置き換えると、JSダイバージェンスの値は0以上～1以下の範囲に収まる。これは、2つの分布が完全に分離している場合の最大値がlog₂(2)＝1となるためである。なお、自然対数を用いた場合でも定義上は問題ないが、そのときの最大値はlog_e(2) ≈ 0.693となる。情報理論や機械学習の分野では、値を「0～1の範囲」に収めた方が直観的に理解しやすいため、対数の底を2とするのが慣例である。

　なお、ここまでの説明では2つの分布PとQを前提としたが、JSダイバージェンスは3つ以上の分布にも拡張できる。一般には、複数の分布を重み付きで混合した分布をMとし、それぞれの分布とのKLダイバージェンスの重み付き平均を取ることで定義される。ただし実際の応用では、特に「2分布間の類似度」を測る用途が圧倒的に多いため、通常は2分布の場合を指して「JSダイバージェンス」と呼ぶ。

「AI・機械学習の用語辞典」