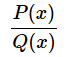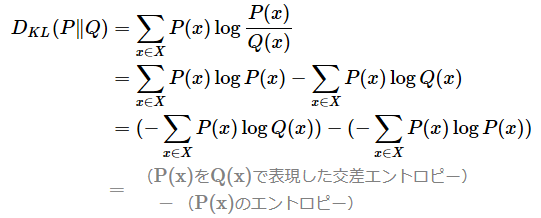KLダイバージェンス(Kullback-Leibler Divergence)/カルバック・ライブラー情報量とは?:AI・機械学習の用語辞典
用語「KLダイバージェンス」について説明。2つの確率分布間のズレを測る指標で、「ある確率分布が別の確率分布とどれだけ異なるか」を評価するために使用される。値が0なら「完全一致」、大きいほど「異なる」ことを意味する。主に統計解析や機械学習モデルの評価、データドリフト検出などで利用されている。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
用語解説
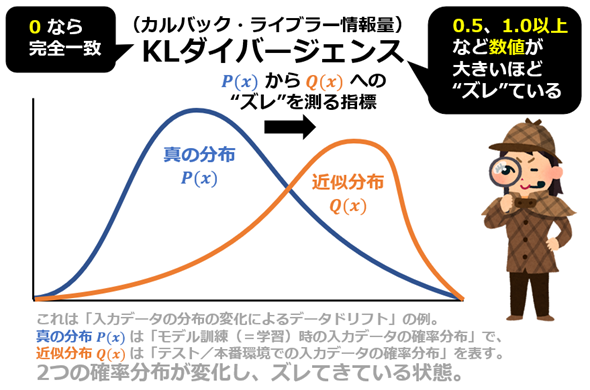
数学/統計学/機械学習におけるKLダイバージェンス(Kullback-Leibler Divergence、別名:カルバック・ライブラー情報量)とは、2つの確率分布間の“ズレ”(=不一致)を測る指標で、「ある分布が別の分布とどれだけ異なるか」を評価するために使用される。例えばPという実際の分布(=真の分布)を、Qという近似する分布(=近似分布)を使って表現しようとした際に、「どれだけ情報が失われるか(=情報損失量)」(言い換えると、完全に表現するために必要な追加の情報量)を計算して評価する(図1)。
KLダイバージェンスの値は、常に0以上の値を取り、0なら「完全に一致する分布」、正の値なら「異なる分布」を意味する。
この値は非対称、つまりPとQの順序を変更することはできない。数学的に表現すると、一般にDKL(P‖Q) ≠ DKL(Q‖P)である。この数式にあるDKL(P‖Q)は、分布Pを基準として分布Qに対する“ズレ”を測るKLダイバージェンスの値を表す。ここでもし順序を入れ替えて DKL(Q‖P)にすると、一般にDKL(P‖Q)とは異なる結果になるというわけだ。KLダイバージェンスは「距離」に似た概念ではあるが、非対称であるため、厳密には距離ではない。
用途
機械学習でのユースケースとしては、モデル訓練時の「入力データ」の確率分布(=真の分布)と、本番環境での「入力データ」の確率分布(=近似分布)が、何らかの変化によってズレてきていることを意味するデータドリフトの検出などに活用される。他にもさまざまな場面で利用されており、例えば、統計モデルや機械学習モデルによる予測(=近似分布)と正解ラベル(=真の分布)の間の誤差(=“ズレ”)を測るために用いられる。また、異なる確率分布同士の類似度を測る手法としても使われており、異常検知、言語モデルの評価、情報検索、確率的モデリングの分野などで幅広く応用されている。
KLダイバージェンスが使われる確率分布
KLダイバージェンスが適用できる確率分布は、大きく2種類に分けられる。
- 離散型確率分布: 主に個数や回数を数え、決まった値しか取らない(例:試験の合格者数、来店者数。合格者数が10.1人のような値はあり得ない)。
- 連続型確率分布: 主に数値の変化を扱い、どんな値でも取れる(例:身長、バスの到着時間。身長が170.1cmのような値もあり得る)。
特によく使われるのは、離散型の「ベルヌーイ分布」「二項分布」、連続型の「正規分布」「指数分布」などである。表1に、KLダイバージェンスが使われる主な確率分布をまとめた。
| 種類 | 確率分布 | 概要 | 利用シーン | |
|---|---|---|---|---|
| 離 散 型 確 率 分 布 |
ベルヌーイ分布 | ある出来事が起こるか起こらないかの2つの結果になる確率を表す分布 | コイン投げで表が出るか裏が出るかの確率、テストで合格するか不合格になるかの確率など、結果が2つしかないような場合に利用する | |
| 二項分布 | ある出来事を何回か行ったときに、特定の回数だけ成功する確率を表す分布 | サイコロを何回か振って1の目が何回出るかの確率、複数人でじゃんけんをして特定の人が勝つ回数など、繰り返しの試行で成功回数を数える場合に利用する | ||
| ポアソン分布 | ある時間や場所で、まれに起こる出来事が何回起こるかの確率を表す分布 | 1時間当たりのお店への来客数、1カ月当たりの交通事故の件数など、めったに起こらない出来事の発生回数を予測する場合に利用する | ||
| 幾何分布 | ある出来事が初めて成功するまでに何回試行する必要があるかの確率を表す分布 | コインを投げて初めて表が出るまでに何回投げる必要があるかの確率、ゲームで当たりが出るまで何回引く必要があるかの確率など、初めて成功するまでの試行回数を予測する場合に利用する | ||
| 負の二項分布 | ある出来事が指定した回数だけ成功するまでに何回試行する必要があるかの確率を表す分布 | サッカーの試合で特定のチームが目標の点数を取るまでに何試合する必要があるかの確率、テストで目標の点数を取るまでに何回受験する必要があるかの確率など、目標回数達成までの試行回数を予測する場合に利用する | ||
| 連 続 型 確 率 分 布 |
正規分布 | 平均値付近に多くのデータが集まり、左右対称の形になる確率分布 | クラスのテストの点数分布、身長や体重の分布など、多くのデータが平均値付近に集まるような場合に利用する | |
| 指数分布 | ある出来事が1回起こるまでの時間間隔を表す確率分布 | バスの待ち時間、電球の寿命など、次に何かが起こるまでの時間を予測する場合に利用する | ||
| ガンマ分布 | ある出来事が複数回起こるまでの時間間隔の合計時間を表す確率分布 | お店に2人目の客が来るまでの待ち時間、機械が3回故障するまでの時間など、複数回の出来事が起こるまでの時間を予測する場合に利用する | ||
| ベータ分布 | 「ある出来事が起こる確率」自体がどの範囲にありそうかを表す確率分布 | 「A/Bテストでどちらの広告がクリックされやすいか」の予測、「商品の売れる確率」の推定など、試行回数やデータによって確率が変動する場合に利用する | ||
| ワイブル分布 | 製品の寿命や故障時間など、時間がたつにつれて壊れやすくなるような現象が発生する時間を表す確率分布 | 機械の寿命予測、部品の耐久性評価など、時間経過に伴う故障や寿命を予測する場合に利用する | ||
| 表1 KLダイバージェンスが使われる確率分布の一覧 | ||||
これらの確率分布について詳しく知りたい方は、連載『社会人1年生から学ぶ、やさしい確率分布【Excelで学べる】』を参考にしてほしい。
定義と数式
KLダイバージェンスを定義する数式は、確率分布の種類(離散型/連続型)によって異なる。前提条件として、
という2つの確率分布があるとする。
離散型確率分布(Discrete Probability Distribution)の場合
離散型(例えばサイコロやコイン投げなど)の場合、この2つの確率分布のKLダイバージェンス、すなわち「真の分布(P)を近似分布(Q)で表現しようとした際の情報損失量」を求める数式は、以下のように表される。なお、数式内の数学記号は後述の箇条書きを参考にしてほしい。
- DKL …… 「KLダイバージェンス」(=カルバック・ライブラー情報量)を指す。
- ‖ …… 「比較対象の区切り」を表す。例えば(P ‖ Q)は「Pを基準にQとの違いを測ること」を意味する。
- Σ …… 「総和」を表す。つまり、その右側で計算した値を合計すること。
- ∈ …… 「集合に属する」(=集合の要素であること)を表す。例えばx ∈ Xは「集合Xに属する値x」を意味する。
- log …… 「自然対数」(=ln、つまりネイピア数eを底とする対数)を表す。
- P(x) …… 「確率分布Pでのxにおける確率」を意味する。Q(x)も同様なので説明は割愛する。
この数式の右端にある分数式では、真の分布での確率(P(x))を近似分布での確率(Q(x))で割ることで確率分布PとQの「比率」を計算している。この比率が1なら完全一致だが、1より上ならQの確率を過小評価し、1より下なら過大評価していることを示す(※比率は0以上であり、0未満にならない)。つまり、
という計算式は、「QがどれだけPに対して誤った確率を与えているか」の指標となっている。この指標に対して自然対数(log)を取ることで、比率を「対数スケール」に変換している。
比率が1なら、その対数変換値はlog 1=0となる。比率が1より上で、例えば2なら対数変換値はlog 2≈0.693と正になり、比率が大きくなるほど対数変換値は緩やかに大きくなる。比率が1より下で、例えば0.5なら対数変換値はlog 0.5≈-0.693と負になり、比率が小さくなるほど対数変換値は急激に小さくなる。このように対数変換することで、比率が1のときを「“ズレ”なし」の基準として、正と負で対称的に“ズレ”を表現できるようにしている。
さらに、この対数変換値にP(x)を掛ける(=重み付けする)ことで「その“ズレ”の重要度」を考慮する。P(x)が大きいほど、その“ズレ”は重要なものと見なされ、P(x)が小さいほど、影響は小さくなる。
最後に、全てのxに対して、以上のように計算した値を合計(=総和)することで、「ある分布Pが別の分布Qからどれだけ異なるか」を評価できる、というわけだ。
ただし、Q(x)が0の場合、分母が0となり計算エラーとなるため、Q(x)が0になる場合には、「極小値を加える」などの数値計算上の対策を講じる必要がある。また、KLダイバージェンスの値は(前述した通り)常に0以上となることが知られており、数学的にはイェンセン(Jensen)の不等式(対数関数の凸性に基づく)により証明されている。
ちなみに、先ほど「真の分布での確率(P(x))」と表現したが、離散型確率分布の場合、このP(x)は、確率質量関数(PMF:Probability Mass Function)である。確率質量関数は総和(Σ)によって確率を計算できる。
一方、次に説明する連続型確率分布の場合、このP(x)は、確率密度関数(PDF:Probability Density Function)である。確率密度関数は積分(∫)によって確率を求める、という違いがある。なお確率質量関数や確率密度関数について詳しく知りたい場合は、『やさしい確率分布』の第1回を参照してほしい。
連続型確率分布(Continuous Probability Distribution)の場合
連続型(例えば身長の分布など)の場合、2つの確率分布のKLダイバージェンス、すなわち「真の分布(P)を近似分布(Q)で表現しようとした際の情報損失量」を求める数式は、以下のように表される。なお、数式内の数学記号のうち、説明していないものを箇条書きで後述した。
- ∫−∞∞ …… 「積分」を表す。つまり、その右側で計算した値を、指定された範囲(この例では−無限大〜無限大)で積分すること。
- dx …… 積分の対象となる1つの小さな単位で、変数xでの「微小な変化量」を表す。例えば∫ f(x)dxは、「関数f(x)をxについて積分すること」を意味する。
この数式は、先ほどの離散型の場合とほぼ同じである。総和(Σ)が積分(∫)に変わっている点のみが異なるが、これは、既に説明したように、連続型確率分布では確率密度関数を用いるので積分する必要があるからだ。よって、数式内容の説明は割愛する。
情報理論からの視点
KLダイバージェンスは、別名で相対エントロピー(relative entropy)とも呼ばれる。
ちなみに、情報理論におけるエントロピー(entropy)は、確率分布の「情報量の期待値」(=得られる情報量の平均)を表し、分布の不確実性を測る指標である。……と少し難しそうな単語が並んでいるので、さらにかみ砕いて言うと、「確率分布が、どれくらい均等に広がっているか、それとも特定の値に偏っているか」を表す数値である。確率分布の確率が満遍なく均等に散らばっている(=どの結果も同じ確率で起こる、例えば棒グラフの全ての列の高さが等しい一様分布の)場合はエントロピーが高く、一部の結果に偏っている(=1つの結果が極端に高い確率で起こる、例えば棒グラフの1列だけが100%の)場合はエントロピーが低くなる。直感的にイメージするなら、エントロピー(=分布の不確実性)を「天気予報の不確実性」に例えると分かりやすく、例えば「晴れ50%、雨50%」ならどちらになるか分からず(=高エントロピー)、「晴れ99%、雨1%」ならほぼ確実に晴れる(=低エントロピー)という状況を想像すればよい。
先ほど示した、離散型の場合のKLダイバージェンスの数式は、以下のように変形することもできる。ちなみに、KLダイバージェンスが対数(log)スケールを取るもう一つの理由は、以下の数式が示すように、確率の比(割り算)を引き算の形に変換できるので、計算しやすくなるメリットがあるからだ。
変形後の式を見ると、相対エントロピー(=KLダイバージェンス)は、「真の分布P(x)を近似分布Q(x)で表現した交差エントロピー(cross entropy)」と「真の分布P(x)のエントロピー」の差(=“ズレ”)としても表せる。この場合、相対エントロピーは、確率分布の違いによる「追加の情報量」(=冒頭で述べた「完全に表現するために必要な追加の情報量」と同じ概念)として解釈できる。
ニューラルネットワークなどの機械学習で広く使われる損失関数「交差エントロピー誤差」も、この考え方がベースになっている。特に、機械学習での正解ラベルがone-hot表現(=1つのクラスのみが1、他は0)である場合、交差エントロピー誤差の計算はKLダイバージェンスと形式的に一致する。one-hot表現の場合、不確実性がない(簡単に言うと、1つの結果に完全に決まっている)ため、「真の分布P(x)のエントロピー」は0になる。よって、「KLダイバージェンス」=「真の分布P(x)と近似分布Q(x)で表現した交差エントロピー」になるわけである。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ