第5回 RDBMSで使われるB木を学ぼう

B木への要素の追加（葉の場合）

　それでは、B木への要素の追加について、より細かく見ていくことにします。

　まず、追加する値が与えられた場合、節点が葉である場合とそうでない場合で処理が異なります。その節点が葉であるかどうかは、子の節点を保持しているかどうかで判断ができます。節点が葉の場合には、ここにはすべてnilがはいっていますし、一番左から埋めていくところなので、一番左のポインタをチェックすればよいことになります。

　葉のバケットにキーを追加する場合、バケットに空きがあればキーの大小関係を壊さないようにして新しいキーを追加します。

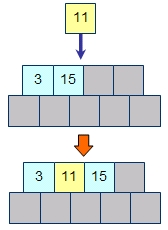
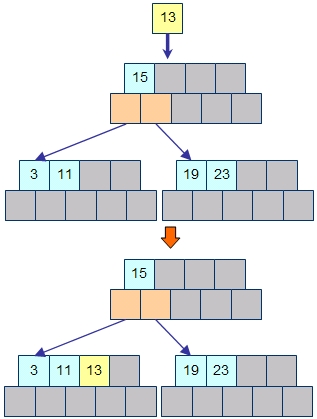
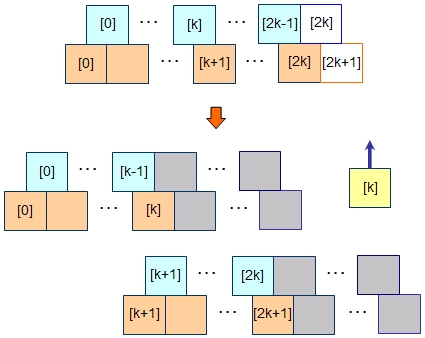
　バケットがいっぱいであればバケットの分割が発生します。K次のB木には2×K個のキーがバケットに入っていて、そこにキーを1つ追加するわけですから、キーをソートしておいた場合には、0から数えてK個目のキーが中央値となります。

　まず、この中央値を親の節点に返します。また、新しいバケットを生成して、そこへK＋1番目から2×K番目までの要素を移します。そして、この新しいバケットへのポインタも一緒に親の節点へ返します。

　呼び出した親の側には新たに先ほどのK番目のキーが渡ってくるので、これをしかるべき位置に挿入し、その右側の子を示すポインタとして新たに生成したバケットへのポインタを格納します。

　こうすると、葉のバケットに対してキーを追加したことからバケットの分割が発生し、それが呼び出した側へと戻ってきて全体の構成がしかるべく調整されます。

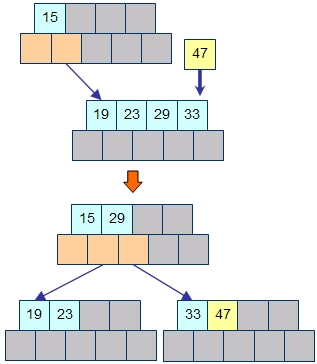
　また、値が戻された際に親の節点のバケットもいっぱいだった場合には、ここでもバケットの分割が発生して、1つ上のレベルの親の節点へと連鎖します。バケットに1つの余裕もなくぱんぱんの場合には、最悪のケースですがルートまで連鎖して、ルートの分割が発生してツリーが一段高くなります。これがB木が高くなるたった1つのケースとなります。

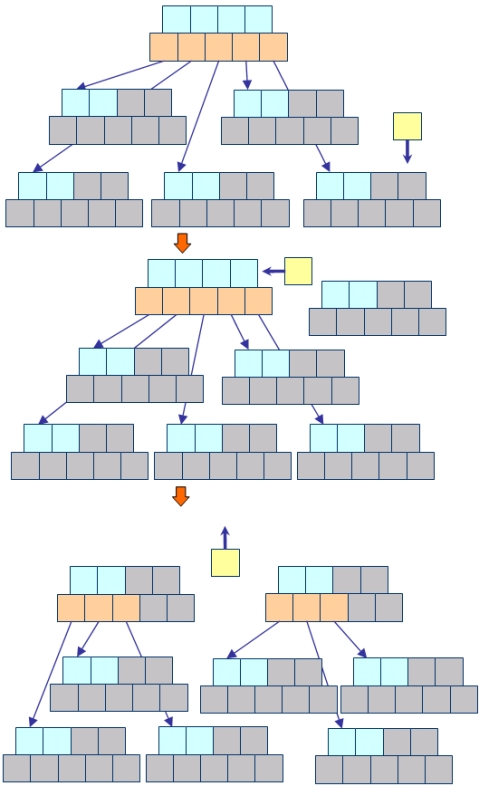
B木への要素の追加（葉でない場合）

　次に、葉でない節点への要素について見ていきます。便宜上、この節点を中間ノードと呼びますがルートについても基本的に同じ操作になります。

　中間ノードにキーを追加する場合、キーの大小をチェックしていって、追加されたキーより大きなキーがあればその左側の子節点へ、大きなキーがなければその右側の子節点へ与えられたキーを追加します。

　中間ノードの場合には、節点に空きがあったとしてもそこに直接新しいキーを追加することはありません。例えば、4つのキーを格納できる2次のB木の場合、3つのキーが格納されている中間ノードの一番大きなキーよりさらに大きなキーが追加されたら、一番大きなキーの右側の子節点へ新しいキーを追加します。

　その結果として右側の子節点でバケットの分割が起こった場合、その中央値が返されてくるのでそれを4つめのキーとして登録し、分割によって新しく生成されたバケットを一番右側の子節点へのリンクとして登録することになります。

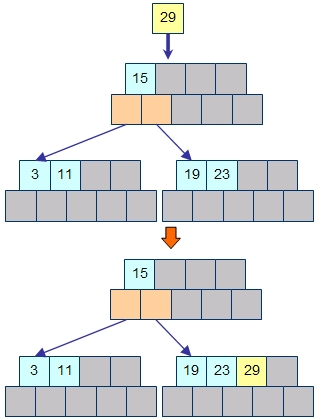
　ルートノードの場合も基本的には中間ノードと同じように与えられた新しいキーを直接登録することはありません。しかし、ルートノードがすでにキーで埋まっている場合に、下位の節点でバケットの分割が起きると、当然、中央値が1つ返ってくるのでルートノード自体も分割しなくてはならなくなります。

　この場合、新しくルートノードを生成し、そこに元のルートノードの中央値を1つだけ登録して、元のルートノードをその左側の子節点として、また新たに生成したバケットを右側の子節点として登録することでバランスを回復します。

B木の実装の工夫

　前回まで解説していたAVL木では、TAVLTreeクラスにTAVLNodeクラスが多数数珠つなぎになるような構造の中で、TAVLTreeクラス側にロジックを集中して書くようにしました。

　B木の実装例でも通常はそうするのですが、今回はTBTreeクラスとTBTreeNodeクラスという2つのクラスのうち、なるべくTBTreeNodeクラス側にロジックを集中するような実装をしてみました。

　こうすることによって、ツリー側の実装で再帰的な処理を書かずに、各オブジェクトを連鎖的に呼んでいるように書けるため、見た目にもすっきりして分かりやすくなるのではないかと思います。

　また、ポインタの編み物を少しでも分かりやすくするために、キーを格納する配列については必要な数＋1を確保するようにして、分割が発生する際にはバケットの最大サイズ＋1までを埋めてから左右に分割するようにしてみました。

　こうすると、確かにメモリと分割時の値の挿入に関する操作時間が無駄になりますが、見た目には分かりやすくなったうえ、プログラムも簡単になります。また、今回のB木のサンプルプログラムではツリーの作成時に次数、つまりバケットの大きさを指定できるようにしてみました。このため、キーを格納する Keys配列と子節点へのリンクを格納する ChildNodes配列はSetLenght()関数で動的にメモリを確保しています。

2/3

Index
RDBMSで使われるB木を学ぼう
	Page1 B木とは何か B木の成長
	Page2 B木への要素の追加（葉の場合） B木への要素の追加（葉でない場合） B木の実装の工夫
	Page3 B木のテストプログラム
	Appendix BTree.pasのソースコード

Delphiアルゴリズムトレーニング

---

Coding Edgeお勧め記事

	いまさらアルゴリズムを学ぶ意味 コーディングに役立つ！ アルゴリズムの基本（1）　コンピュータに「3の倍数と3の付く数字」を判断させるにはどうしたらいいか。発想力を鍛えよう
	Zope 3の魅力に迫る Zope 3とは何ぞや？（1）　Pythonで書かれたWebアプリケーションフレームワーク「Zope 3」。ほかのソフトウェアとは一体何が違っているのか？
	貧弱環境プログラミングのススメ 柴田 淳のコーディング天国　高性能なIT機器に囲まれた環境でコンピュータの動作原理に触れることは可能だろうか。貧弱なPC上にビットマップの直線をどうやって引く？
	Haskellプログラミングの楽しみ方 のんびりHaskell（1）　関数型言語に分類されるHaskell。C言語などの手続き型言語とまったく異なるプログラミングの世界に踏み出してみよう
	ちょっと変わったLisp入門 Gaucheでメタプログラミング（1）　Lispの一種であるScheme。いくつかある処理系の中でも気軽にスクリプトを書けるGaucheでLispの世界を体験してみよう
	more

　　Coding Edgeフォーラムフィード　 2.0／1.0／0.91