レコメンデーションとエディットグラフ:コーディングに役立つ! アルゴリズムの基本(10)(3/4 ページ)
エディットグラフの実装(後半)
引き続きコードを解説します。経路に従って結果表示します。
84 function getDiffString(str1, str2) {
85 var edit_graph = makeEditGraph(str1, str2);
86 var x = 0;
87 var y = 0;
88
89 diff_string = "";
90 while ((x < str1.length) || (y < str2.length)) {
91 switch(edit_graph[x][y].direction) {
92 case EGD_X:
93 diff_string += minus_ch(str1.charAt(x));
94 x++;
95 break;
96 case EGD_Y:
97 diff_string += plus_ch(str2.charAt(y));
98 y++;
99 break;
100 case EGD_XY:
101 diff_string += str1.charAt(x);
102 x++;
103 y++;
104 break;
105 }
106 }
107
108 return diff_string;
109 }
110
111
112 function execDiff() {
113 var text = getStringById('text');
114 var area = getStringById('area');
115 var diff_string = getDiffString(text, area);
116 document.getElementById('diff').innerHTML = diff_string;
117 }
118 </script>
119 <input value="diff" type="button" onClick="execDiff()"></input>
120 <!-- 末尾2 -->
121 <div id="diff"></div>
122
123 </body>
124 </html>
- 90〜106行目
左上からスタートしてedit_graphのdirectionに沿って進んでいきます。
右方向だった場合(EGD_X)、文字が消えているので赤背景横線で文字を表示します。
下方向だった場合(EGD_Y)、文字が増えているので黄色背景で文字を表示します。
斜めだった場合(EGD_XY)、変化がないのでそのまま表示します。
こうして1文字ずつ結果表示用文字列(diff_string)を作っていきます。
より効率的なエディットグラフ
先ほどのアルゴリズムもスマートですが、すべての点について方向とコストを計算しています。より少ない計算回数で解決する方法があります。O(ND)アルゴリズムと呼ばれています。
最短で右下に行くにはできるだけ多く斜めに進めばよいはずです。逆にいえば、縦・横に進む回数を最小にすればよいはずです。そこで縦か横に進んだ回数をDとしてカウントします。
左上からスタートしてDを0から1ずつ進めていきます。
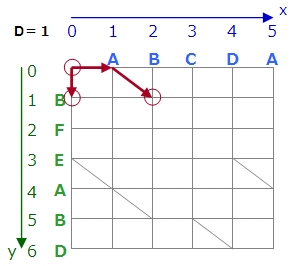
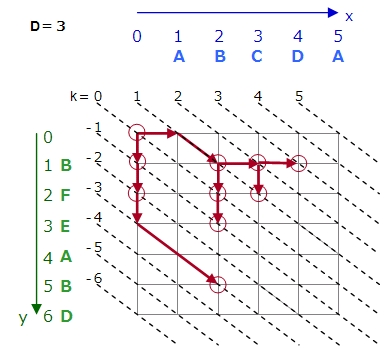
Dが0のときは左上です。
Dが1のときは左上から1つ分だけ進みます。下に1進む場合と、右に1進む場合が考えられます。右に進んだ場合は斜めにも進めます。斜めに進む場合はカウントしませんので進めるだけ進みます。
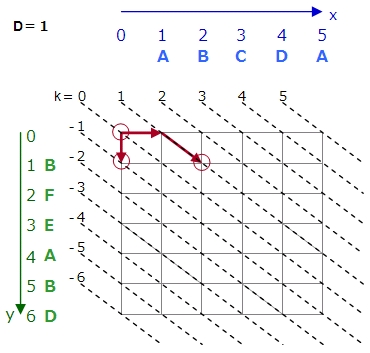
次はD=2の場合を考えます。このとき普通に考えると進んだ点を基準に考えると思いますがそうはしません。グラフの上に斜めの線を引き、その線を基準に考えます。斜めの線にはそれぞれ番号を付けます。左上の点を通る線をk=0の線とします。そこから下の線はk=-1、k=-2……とします。右の線はk=1、k=2……とします。
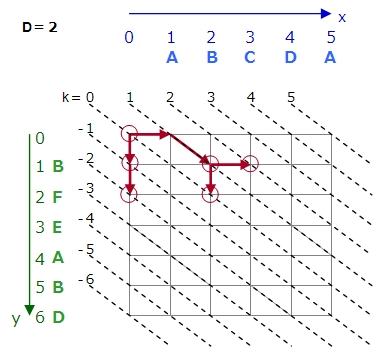
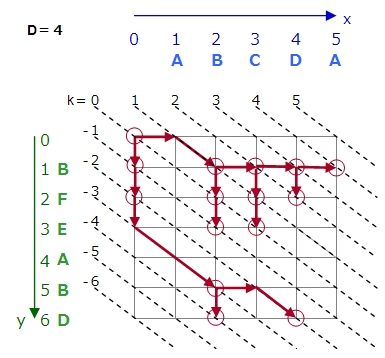
D=2のとき、進んだ点がどの斜線k上にあるかを考えます。
D=2ということは、最大で左上から下に2回進んでいる可能性があるので、k=-2の場合があります。k=-3以下の場合はありません。同様に最大で右に2回行っている可能性があるので、k=2の場合があります。k=3以上の場合はありません。つまりk=-2〜2の範囲を順次考えます。
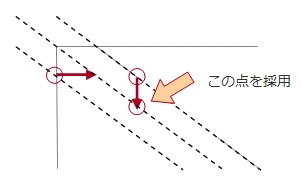
次にそれぞれの斜線上で、どこに点が来るかを考えます。その前後の斜線上の点を、右または下に進めます。より右に来るほうの点を採用します。
さらに斜めに進められる場合は進めます。
なお、斜線はすべて調べる必要はありません。1本おきにチェックすれば大丈夫です。Dが1つ増加するごとに、矢印が下(k-1)または右(k+1)へ1回のみ移動します。そのため、Dが偶数ならば対象となるkも偶数、Dが奇数ならば対象となるkも奇数になり、1本おきのチェックで計算ができます。
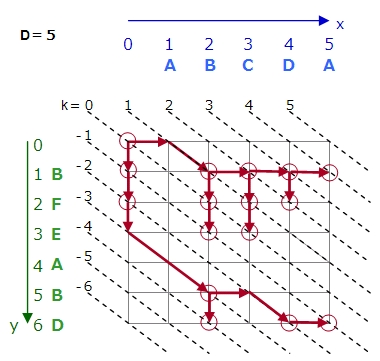
こうしてDを1つずつ進めていき、最初に右下にたどりつくまで繰り返します。
最後に結果を表示するところでは、最初のやり方とは逆に、右下のゴールから左上に向かってたどっていきます。
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ