回帰分析II：重回帰分析の方法、科学的な将来予測：ITエンジニアのためのデータサイエンティスト養成講座（7）（3/3 ページ）

[中林紀彦，＠IT]

未来の電力消費量を予測する

　それではモデル（2）の数式を使って未来の予測をしてみましょう。

　例えば2014年の6月30日（月）から7月4日（金）までの最低気温と最高気温が予測できるとして、“next_year.csv”というファイルに先程のX2の形式でデータが用意されているとします。

date,high,low,const
2014-06-30,28.0,23.0,1
2014-07-01,31.0,23.0,1
2014-07-02,35.0,27.0,1
2014-07-03,33.0,26.0,1
2014-07-04,31.0,20.0,1

　StatsModelsで提供されるpredictというメソッドを使い、電力消費量を予測できます（In [66]）。これは先程のモデル（2）の式に最低気温と最高気温を代入したものと同じです。

［電力消費量］＝［最高気温］×62.9363＋［最低気温］×55.5623＋928.3536

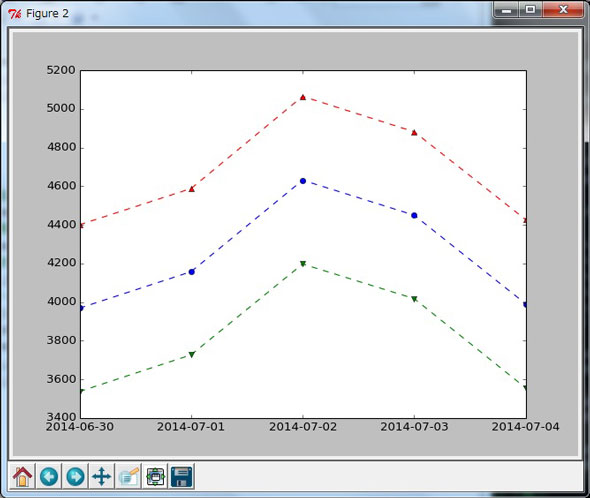
　さらに先ほどのwls_prediction_std関数で予測区間も計算できますので、それぞれをプロットして確認してみましょう（In [69]〜In [74]）。図2がプロットの結果です。

　今回のケースは来年の最低気温と最高気温という非現実的な例をご紹介しましたが、1週間先くらいまでであれば、いろいろな気象予報サービスで提供されているデータがありますので実際の予測にも活用できるはずです。

In [63]: # 最高気温と最低気温の予測を読み込み
In [64]: XN = pd.read_csv('next_year.csv', index_col='date')
In [65]: # 電力消費量を予測
In [66]: pred = results2.predict(XN)
In [67]: # 予測区間をもとめる
In [68]: prstdn, iv_ln, iv_un = wls_prediction_std(results2, XN)
In [69]: # プロット
In [70]: plt.figure()
Out[70]: <matplotlib.figure.Figure at 0x75b0170>
In [71]: plt.xticks(arange(len(XN.index)), XN.index) # x軸の項目名
Out[71]:
([<matplotlib.axis.XTick at 0x75bc570>,
  <matplotlib.axis.XTick at 0x75bcbd0>,
  <matplotlib.axis.XTick at 0x785f9d0>,
  <matplotlib.axis.XTick at 0x785fef0>,
  <matplotlib.axis.XTick at 0x7869450>],
 <a list of 5 Text xticklabel objects>)
In [72]: plt.plot(pred, 'bo--') # 予測値 ： 青色
Out[72]: [<matplotlib.lines.Line2D at 0x7869890>]
In [73]: plt.plot(iv_un, 'r^--') # 予測区間の上限 ： 赤色
Out[73]: [<matplotlib.lines.Line2D at 0x78698b0>]
In [74]: plt.plot(iv_ln, 'gv--') # 予測区間の下限 ： 緑色
Out[74]: [<matplotlib.lines.Line2D at 0x7874090>]

おわりに

　前回と今回の2回にわたって回帰分析について紹介してきました。

　回帰分析の手法を使うと、2つ以上の変数の相関関係を数式で表すことができます。この数式を使って「未来を予測する」ことが可能になり、ビジネス上の意思決定やアクションにつなげることができます。

　ただし繰り返しになりますが、実際の意思決定やアクションを決める場合には、モデルから予測される値以外の考慮も重要な要素になってきますので、数値だけの意思決定にならないように気を付けましょう。

　次回はデータをいくつかのグループに分類するための手法である“クラスタリング（Clustering Analysis）”について詳しく紹介しますのでお楽しみに。