回帰分析II:重回帰分析の方法、科学的な将来予測:ITエンジニアのためのデータサイエンティスト養成講座(7)(2/3 ページ)
電力消費量と最高気温および最低気温の相関関係を重回帰分析する
モデル(1)は、妥当な良いモデルですが、さらに精度を上げるために、モデルを改良していきましょう。改良のプロセスにより、精度を高めていくのは前回と同じです。
夏場でも最低気温が電力消費量の最大値に影響を与えると仮定して、先ほどの仮説を「1日の電力使用量の最大値は最高気温および最低気温と相関関係がある」という仮説に変更し、モデル2を仮定します。
[電力消費量]=[最高気温]×[係数a1]+[最低気温]×[係数a2]+[定数b] ――モデル(2)
説明変数が2つになったので、このモデルは重回帰分析になります。ただし、計算方法は先ほどの単回帰分析と同じです(In [42]〜In [52])。
In [42]: # 最高気温と最低気温を説明変数X2として定義
In [43]: X2 = dfx
In [44]: # 定数項をX2に加える
In [45]: X2 = sm.add_constant(X2, prepend=False)
In [46]: # 電力消費量を目的変数yとして定義
In [47]: y_true = dfy['actual']
In [48]: y = y_true
In [49]: # モデルを定義
In [50]: model2 = sm.OLS(y,X2)
In [51]: # 回帰分析を実行
In [52]: results2 = model2.fit()
In [53]: # 結果のサマリを確認
In [54]: results2.summary()
Out[54]:
<class 'statsmodels.iolib.summary.Summary'>
"""
OLS Regression Results
==============================================================================
Dep. Variable: actual R-squared: 0.830
Model: OLS Adj. R-squared: 0.827
Method: Least Squares F-statistic: 258.7
Date: Sun, 17 Nov 2013 Prob (F-statistic): 1.66e-41
Time: 15:23:45 Log-Likelihood: -739.02
No. Observations: 109 AIC: 1484.
Df Residuals: 106 BIC: 1492.
Df Model: 2
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
high 62.9363 9.652 6.521 0.000 43.800 82.072
low 55.5623 9.651 5.757 0.000 36.427 74.697
const 928.3536 149.729 6.200 0.000 631.501 1225.206
==============================================================================
Omnibus: 0.001 Durbin-Watson: 1.247
Prob(Omnibus): 1.000 Jarque-Bera (JB): 0.067
Skew: 0.003 Prob(JB): 0.967
Kurtosis: 2.878 Cond. No. 266.
==============================================================================
"""
結果を確認すると、係数a1、a2、定数bはそれぞれ、62.9363、55.5623、928.3536 となることが分かりますので、モデル(2)の数式は以下のようになります。
[電力消費量]=[最高気温]×62.9363+[最低気温]×55.5623+928.3536
出力結果を見て分かる通り、決定係数、F検定、t検定の値を見ても、それぞれ問題なく、モデル(2)も良好なモデルであると確認できます。また、決定係数が0.830であり、モデル(1)よりも電力消費量の実測値を良好に表現できているということができます。
“予測区間”からモデルで予測できる範囲を確認
ここまではモデルを作り数式を導く方法やその妥当性や精度について説明してきましたが、ビジネスの現場で“意思決定やアクションにつなげる”ためにはモデルから導き出された数式を使った“未来の予測”が重要となります。そのため「モデルから計算される値がどの範囲にあると予測されるか」が大きな問題の1つとなってきます。
これは統計学の用語で”予測区間”(リンク)と呼ばれていて、StatsModelsで提供されるwls_prediction_std関数を使って計算することができます。
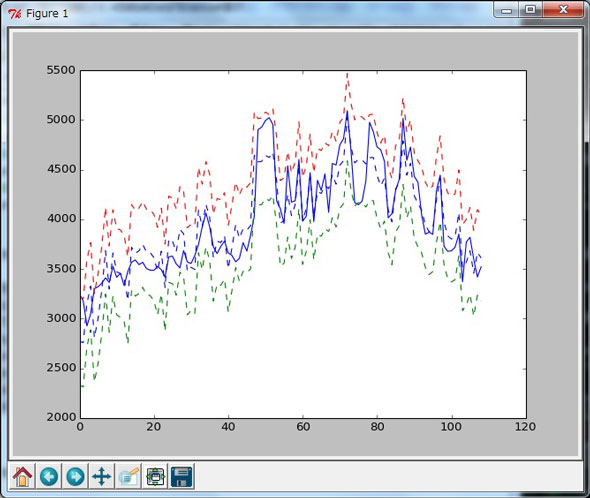
In [56]ではwls_prediction_std関数を使って予測区間の下限(iv_l)と上限(iv_u)を求めています。それぞれの値をグラフにプロットすると(In [58]〜In [62])、図1のようになります。
今回のモデル(2)では5月から9月の実測値は予測区間に含まれる値となっていますので、電力消費量の最大値を予測して意思決定やアクションをする場合には、予測される値は予測区間内にあるという前提で利用します。
特に電力消費量のように最大値の予測を超えるような利用があると大きなインパクトがある場合などは、さらにマージンを検討するなど、モデルから予測される値以外の考慮も重要な要素になってきますので、数値だけの意思決定にならないように気を付けましょう。
次ページでは、ここまで解説した内容を踏まえ、どのように将来を予測していくかを紹介します。
In [55]: # 予測区間の確認 In [56]: prstd, iv_l, iv_u = wls_prediction_std(results2) In [57]: # プロット In [58]: plt.figure() Out[58]: <matplotlib.figure.Figure at 0x733a930> In [59]: plt.plot(y_true, 'b-') # 実測値 : 青色の実線 Out[59]: [<matplotlib.lines.Line2D at 0x7509ed0>] In [60]: plt.plot(results2.fittedvalues, 'b--') # モデルから予測される値 : 青色の点線 Out[60]: [<matplotlib.lines.Line2D at 0x7514890>] In [61]: plt.plot(iv_u, 'r--') # 予測区間の上限 : 赤色の点線 Out[61]: [<matplotlib.lines.Line2D at 0x7514f30>] In [62]: plt.plot(iv_l, 'g--') # 予測区間の下限 : 緑色の点線 Out[62]: [<matplotlib.lines.Line2D at 0x751e650>]
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ