時系列分析II―ARMAモデル（自己回帰移動平均モデル）の評価と将来予測：ITエンジニアのためのデータサイエンティスト養成講座（10）（2/4 ページ）

[中林紀彦，日本アイ・ビー・エム]

モデルの選択

　最適なモデルの選択の評価基準として一般的によく用いられるのが、赤池情報量規準（AIC：An Information Criterion、のちにAkaike's Information Criterion）もしくはベイズ情報基準（BIC：Bayesian Information CriterionもしくはSIC：Schwarz Information Criterion）です。

赤池情報量規準：AIC（Akaike's Information Criterion）

　AICは下記の式1で求めることができる値です。

　式の第1項がモデルへの当てはまりの良さを、第2項がモデルの複雑さに対するペナルティを表します。モデルの「もっともらしくなさ」と「ムダさ」を示しています。

　第2項は、パラメーター数が少ない方がオーバーフィッティング（Overfitting）問題を避けることができるので、パラメーター数を押さえたモデルに優位に働きます。

　対象となる全てのモデルでAICを計算して最小となるモデルを選択すると一般的には良いモデルが選択できるといえます。

式1　AICを求める式（Wikipediaから引用）

BIC（Bayesian Information Criterion）

　BICはAICと同様ですが、標本数が多くなると必ず正しいモデルを選択するという特徴があります。

式2　BICを求める式（Wikipediaから引用）

　しかし、AICもBICも絶対に正しいということはありませんので、一般的にはAICとBICの両方の情報量基準を評価してモデルを選択するというアプローチが多いようです。今回もそれぞれのモデルにおけるAIC、BICを算出し（In [36]〜In [42]）、および表1にまとめてみました。これを見ると、[OUT 39]の結果がAIC、BICともに最小になっていることからARMA(13,0)モデルを選択するのが良いと思われますので、今回はARMA(13,0)を採用したいと思います。

In [36]: # 情報量基準（AIC、BIC）の確認
In [37]: arma_mod1100.aic, arma_mod1100.bic
Out[37]: (1224.8178002098773, 1261.0551928660439)
In [38]: arma_mod1200.aic, arma_mod1200.bic
Out[38]: (1180.0111144107414, 1219.03599880969)
In [39]: arma_mod1300.aic, arma_mod1300.bic
Out[39]: (1173.5601565347606, 1215.3725326764913)
In [40]: arma_mod1101.aic, arma_mod1101.bic
Out[40]: (1204.7565755255855, 1243.7814599245341)
In [41]: arma_mod1201.aic, arma_mod1201.bic
Out[41]: (1176.025440381647, 1217.8378165233778)
In [42]: arma_mod1301.aic, arma_mod1301.bic
Out[42]: (1174.0475587270212, 1218.647426611534)

表1　AIC、BICによるモデル評価を表にまとめたもの

モデルの妥当性

　次に選択したモデル、AR(13)の妥当性を検討してみたいと思います。

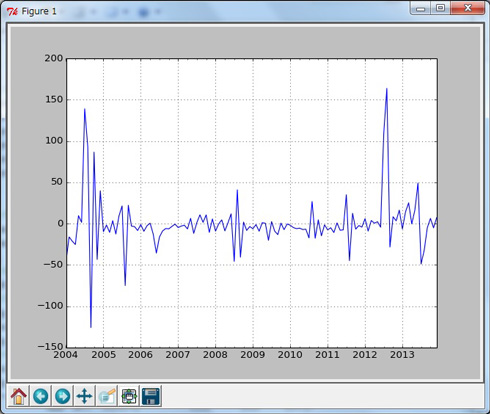
　妥当性の検討には“残差”を用いますので、まずは残差をグラフで表示して確認しておきます。

　残差とは「実測値」と「モデルから算出される値」との差分のことです。残差はresidを使って簡単に算出することができます（In [43]〜In [45]）。

　図3を見ると多少差が大きなところも見受けられますが、おおむね良好な値を示しています。

In [43]: # 残差の算出とグラフ表示
In [44]: resid = arma_mod1300.resid
In [45]: resid.plot()
Out[45]: <matplotlib.axes.AxesSubplot at 0x8348110>

図3　ARMA(13)の残差グラフ