時系列分析II―ARMAモデル（自己回帰移動平均モデル）の評価と将来予測：ITエンジニアのためのデータサイエンティスト養成講座（10）（1/4 ページ）

過去の時系列データを基に、将来予測につながるモデルを検討、実際に将来予測を行って検証してみましょう。

[中林紀彦，日本アイ・ビー・エム]

連載バックナンバー

はじめに

　前回は、時系列分析の代表的なモデルの1つであるARMAモデル（自己回帰移動平均モデル）について、パラメーターを変化させながらサンプルデータを生成させてモデルの特徴を確認してみました。

　今回は、実際のデータを使いARMAモデルのパラメーターを推定し、未来の予測に活用するような実例を紹介したいと思います。

　ARMAモデルの詳細は前回解説していますので、参照してください。

　なお、本連載が前提とする環境の構築方法や基本的な使い方は連載第1〜4回で紹介しています。個別の分析手法と実践的な使い方については第5回以降で解説しています。本稿の解説はこれらの環境を踏まえたものですが、一部、Python実行環境や利用しているライブラリ類はアップデートをしていますので、適宜ご自身の環境に置き替えて読み進めてください。

Google トレンドのキーワードを分析

　今回は「Googleトレンド」のキーワードをサンプルにARMAモデルを使ってトレンドの予測をしてみたいと思います。

　下準備として、あらかじめGoogleトレンドから「夏休み」というキーワードのトレンドを“report.csv”というファイル名でダウンロードしておきましょう。

ウェブ検索の人気度: 夏休み
すべての国; 2004年 - 現在
人気度の動向
週,夏休み
2004-01-04 - 2004-01-10,9
2004-01-11 - 2004-01-17,3
2004-01-18 - 2004-01-24,5
2004-01-25 - 2004-01-31,6
2004-02-01 - 2004-02-07,6
2004-02-08 - 2004-02-14,6
2004-02-15 - 2004-02-21,4
〜 以下省略 〜

　Googleトレンドでキーワード「夏休み」のデータを取得（report.csv）

データの準備

　それではPythonを使って実際に時系列分析を行ってみましょう。

　必要なライブラリを読み込んで（In [1]〜In [5]）サンプルデータを読み込みインデックスを付与（In [7]〜In [8]）し、必要のない列を削除し列名を変更します（In [9]〜In [10]）。

　ダウンロードしたままのreport.csvデータは週次のデータになっていますので、月次データにダウンサンプリングし、グラフに表示して内容を確認します（In [12]〜In [13]）。

In [1]: # 必要なライブラリの読み込み
In [2]: %pylab
Using matplotlib backend: TkAgg
Populating the interactive namespace from numpy and matplotlib
In [3]: import pandas as pd
In [4]: from scipy import stats
In [5]: import statsmodels.api as sm
In [6]: # サンプルデータの読み込みと時系列インデックスの付与
In [7]: df = pd.read_csv('report.csv', skiprows=5, header=None, nrows=550)
In [8]: df.index = pd.date_range('2004-01-04', periods=550, freq='W')
In [9]: del df[0]
In [10]: df = df.rename_axis(mapper={1:'num'}, axis=1)
In [11]: # 週次データから月次データへのダウンサンプリングとグラフ表示
In [12]: dfm = df.resample('M', how=sum)
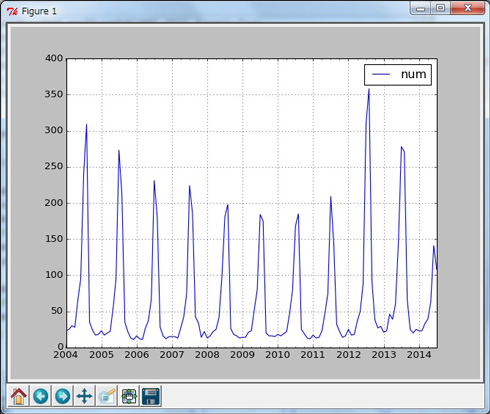
In [13]: dfm.plot()
Out[13]: <matplotlib.axes.AxesSubplot at 0x7a6e210>

　当たり前ですが、季節性のあるキーワードなので、図1のように周期のある時系列データであることが確認できます（図1）。

図1　report.csvのダウンサンプリング結果

モデルの推定

　このデータをARMAモデルに当てはめていくわけですが、後で2014年の数値を予測して実際の値と比較してみたいと思いますので、ここでは2013年までのデータを切り出して使用します（In [17]）。

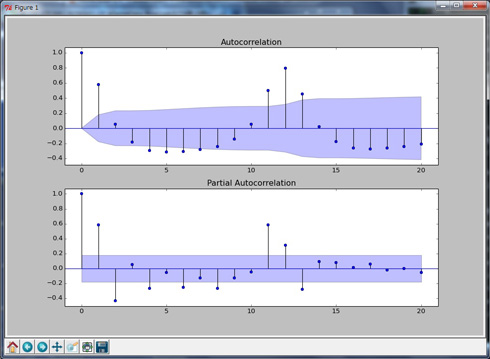
　第9回「時系列分析Ｉ ――ARMAモデルと時系列分析」で紹介したようにARMAモデルの推定には、自己相関（Autocorrelation）プロットと偏自己相関（Partial Autocorrelation）プロットを利用します（In [18]〜In [25]）。

　ARMA(p,q)モデルの場合、偏自己相関プロットからpの値を、自己相関プロットからqの値を類推します。

In [14]: # 前のグラフを閉じる
In [15]: plt.close()
In [16]: # モデル作成に使用するデータの切り出し
In [17]: dfms = dfm[dfm.index <= '2013-12-31']
In [18]: # 自己相関（Autocorrelation）プロット
In [19]: fig = plt.figure(figsize=(12,8))
In [20]: ax1 = fig.add_subplot(211)
In [21]: fig = sm.graphics.tsa.plot_acf(dfms['num'], lags=20, ax=ax1)
In [22]: # 偏自己相関（Partial Autocorrelation）プロット
In [23]: ax2 = fig.add_subplot(212)
In [24]: fig = sm.graphics.tsa.plot_pacf(dfms['num'], lags=20, ax=ax2)
In [25]: fig.show()

　図2の自己相関（Autocorrelation）および偏自己相関（Partial Autocorrelation）プロットの青色の部分は95％（plot_acf、plot_pacfのデフォルト値。パラメーターで変更可能）の「信頼区間」を示しています。下側の偏自己相関プロットを見るとラグ値13以降の値は、信頼区間内にあるので「相関性がない」と判断できます。よって、pは11、12、13のいずれかの値と類推します。また、上側の自己相関プロットから、ラグ値1および11、12は信頼区間よりも大きく外側にあることから、相関性がありそうだと類推できるのですが、今回は「移動平均の影響は短期」という仮定を置き、qは0もしくは1と類推します。

図2　自己相関プロットと偏自己相関プロット

　こうして偏自己相関と自己相関プロットから類推したpとqにより以下の6つのモデルが候補として挙げられます。

ARMA(11,0)、ARMA(12,0)、ARMA(13,0)、ARMA(11,1)、ARMA(12,1)、ARMA(13,1)

自己相関、偏自己相関プロットの結果から類推できるモデル候補

　実際にモデルのパラメーターを推定して（In [28]〜In [35]）最適なモデルを選択してみましょう。

In [26]: # 前のグラフを閉じる
In [27]: plt.close()
In [28]: # ARMA(11,0), ARMA(12,0), ARMA(13,0)モデルの推定
In [29]: arma_mod1100 = sm.tsa.ARMA(dfms, (11,0)).fit()
In [30]: arma_mod1200 = sm.tsa.ARMA(dfms, (12,0)).fit()
In [31]: arma_mod1300 = sm.tsa.ARMA(dfms, (13,0)).fit()
In [32]: # ARMA(11,1), ARMA(12,1), ARMA(13,1)モデルの推定
In [33]: arma_mod1101 = sm.tsa.ARMA(dfms, (11,1)).fit()
In [34]: arma_mod1201 = sm.tsa.ARMA(dfms, (12,1)).fit()
In [35]: arma_mod1301 = sm.tsa.ARMA(dfms, (13,1)).fit()