「27°C×2=54°C」が何の意味もない理由とは――「測定」と「データ」の基礎知識:「AI」エンジニアになるための「基礎数学」再入門(2)(1/2 ページ)
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す連載。今回から具体的に数学を学ぶと予告しましたが、まずは「測定」と「データ」の基礎知識について押さえておきましょう。
私たちは“測定”を毎日行っている
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す本連載『「AI」エンジニアになるための「基礎数学」再入門』。初回は、「AIエンジニア」になるために数学を学び直す意義や心構え、連載で学ぶ範囲についてお話ししました。今回から具体的に数学を学ぶと予告しましたが、まずは「測定」について理解する必要があります。
そもそも統計や機械学習(AI)を用いて問題を分析する際には、問題に関する情報を「データ」として持っていなければいけません。つまり、現象を数字なり文字なりの値に“変換”(測定)してある必要があります。これは、特に難しいことではなく、例えば店で何かを買うときにレジに表示される数字は、支払わなければならない金額の“測定”値です。それから、体重計に乗った際に目にする数字は、その人の体重の“測定”値です。このように、私たちは“測定”を当たり前のように毎日行っていながら生活をしています。
データは、分析しやすければ、数字である必要はありません。例えば、「男性」と「女性」というカテゴリーは、人々を分類するのに広くに用いられていますが、「数」ではありません。同じように、色は「赤」や「青」といったようにさまざまにカテゴリー化されていますが、これも「数」ではありません。ところが、色は時に「カーマイン」「クリムゾン」といったように、より細かくカテゴリー化される場合があります。カテゴリーにおける詳細さは、分類を行う理由と用途に基づいて変化することもあります。
データ分析には、「データを集めて、ためて、活用する」という流れがあります。その中で、“測定”の概念は「集める」のフェーズには当然関係しますが、「活用」のフェーズでも「XXデータはXXな測り方なので、XXという前処理を施してから分析をしよう」といった具合に、意識されることが多々あります。このように、どのフェーズにも一貫して関係する重要かつ基礎的な概念ですから、しっかりと要点を押さえておきましょう。
データの種類
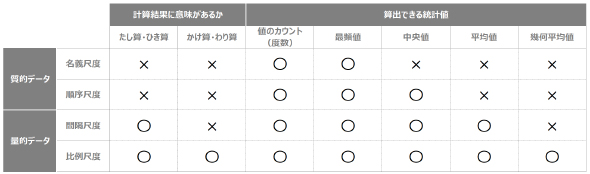
データは、大まかに2種類――計算(加減乗除など)をしても意味がない(質的)データか、意味がある(量的)データか――、細かくは4つの尺度(図1)に分類できます。それぞれに特徴があり、それによって考慮しなければいけない手続きも変わってきます。
質的データ
分類や種別を判別するための値のことを、「質的データ」(カテゴリーデータ)と呼びます。質的データの特徴は「計算の結果に意味がない」という点です。大抵は数字ではなく文字として値が入っています。
クロス集計(表1)のカテゴリーとして、用いる際には問題ありませんが、機械学習(AI)に用いる際は気を付けなければいけません。なぜならば、機械学習は数字の計算を繰り返し行うことが必要になるため、「文字→数字」の変換が必須だからです。このように、普通のデータ――普通は「数字」をイメージされることでしょう――よりも用心することが多いのが質的データなので、その性質と利用方法まで確認しましょう。
| はい | いいえ | 計 | |
|---|---|---|---|
| 男性 | 100 | 50 | 150 |
| 女性 | 200 | 100 | 300 |
・名義尺度
「名義尺度」は、単に物を識別するために割り当てられた値のことを言います。例えば、上記の男性/女性や赤色/青色といった区別など、大小関係のないデータを「名義尺度」と呼びます。
「大小関係がない」とは、どういうことなのでしょうか? 表2を見て確認して見ましょう。
| 性別(1:男性、2:女性) | …… |
|---|---|
| 2 | …… |
| 1 | …… |
| 2 | …… |
| …… | …… |
実務の中で、表2のようなデータは一般的にあります。このように、1や2という数字だけで考えれば大小関係はありますし、それで考えれば計算はできるものの、結果が意味を持たないデータ――「2+1=女性+男性=3」に意味は見いだせません――を名義尺度と呼びます。
また、当然と言えば当然ですが、名義尺度は平均値や中央値(※平均などの統計量については、次回記事で詳しく解説します)を算出することに意味がありません。ただし、最頻値(最も出現頻度の高い値)を求めることには意味があります。
・順序尺度
続いて、名義尺度と似て非なるものに、順序尺度というものがあります。順序尺度とは名前の通り、その値の順序には意味があります。すなわち、低い値より高い値は何らかの特性が強いということです。しかし、名義尺度と同様に計算の結果が意味を持ちません。具体的にどういうデータなのか、表3で確認してみましょう。
| アンケート結果(0:嫌い、1:普通、2:好き) | …… |
|---|---|
| 2 | …… |
| 1 | …… |
| 0 | …… |
| 1 | …… |
| …… | …… |
このデータを例にして見ると、確かに2(好き)は1(普通)よりも、好感度が高いという意味を見いだせます。しかし、こちらも名義尺度と同じように、安易に計算をしてはいけません。なぜならば、順序尺度には「等間隔性」がないからです。
どういうことかと言いますと、例えば表3のデータを用いて、「2-1=1」「1-0=1」という2つの引き算から1という値が2つ得られたとします。このとき、左側の1は「好き」と「普通」の好感度の差を表す1だと解釈できます。一方で、右側の1は「普通」と「嫌い」の好感度の差を表す1だと解釈できます。さて、この2つの1は同じものだと言い切ることはできるでしょうか?
この場合、言い切らない方が無難でしょう。このアンケートの0(嫌い)は飛び切り好感度が低い状態を表していたり、2(好き)は限りなく普通に近かかったりするかもしれません。つまり、嫌いと普通の間には大きな距離があって、普通と好きは紙一重であることもなくはないわけです。このような理由から、一見して計算できてしまいそうな順序尺度ではありますが、扱いに気を付けなければいけません。
量的データ
量的データは、質的データとは一転して、「数字として意味があり、計算できる」という特徴があります。つまり、値としては当然ながら数字で、各数字間の間隔も一定――例えば、10円と11円の差と、100円と101円の差の1円はどちらも同じ大きさ(価値)――です。
以下の表4で例示するデータの列は全て量的データです。この中には、量的データに属する間隔尺度と比例尺度(図1)という2つの尺度のデータが存在しています。それぞれ、どのような特徴なのか、どこに気を付けなければいけないのかを確認しましょう。
| 気温(°C) | 売上(円) | …… |
|---|---|---|
| 27 | 315,234 | …… |
| 25 | 248,723 | …… |
| …… | …… | …… |
・間隔尺度
間隔尺度は、数字として意味があり、等間隔性もあるものの、「0という値が何もない状態を示してい“ない”」という特徴があります。そして、間隔尺度は足し算と引き算に限り計算することができますが、掛け算や割り算はできないので、注意が必要です。
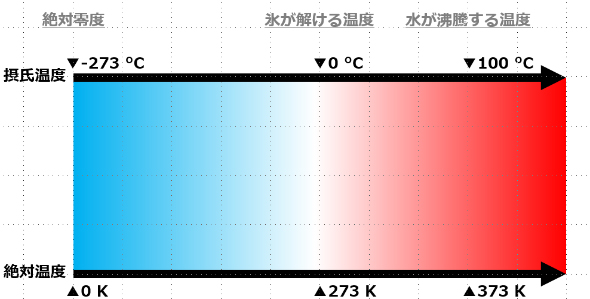
これについては、私たちにとってなじみのある温度(図2)を例に考えてみましょう。
図2から分かるように、私たちが普段目にする温度(セ氏温度)は、氷が解ける温度に0というキリの良い基準を置く仕様になっています。よって、セ氏温度の0°Cは絶対温度で確認してみると熱がある状態になるわけです。
このように、0が何もない状態ではないセ氏温度をはじめとした間隔尺度は、掛け算や割り算ができません。例えば、セ氏温度の27°Cに2を掛けると、54°Cという計算結果になりますが、絶対温度で考えてみると、300K→327Kとなっており、2を掛けたにもかかわらず値が2倍になっていないことが分かります。こういった理由から、間隔尺度は掛け算および割り算をした結果に意味を持ちませんので、注意が必要です。
・比例尺度
一方の比例尺度は、0という値が何もない状態を示す尺度です。これに分類されるデータは世の中に多く存在しています。以下がその例です。
- 絶対温度(図2)
- 売上や利益などの金額
- 行動回数(アクセス回数、ログイン回数、購入回数など)
これらのデータは、0という値が何もない状態を示していることで、足し算と引き算に加えて、掛け算と割り算も有効です。図2の絶対温度を例に考えてみると、300Kに2をかけた結果は600Kとなります。明らかに2をかけた結果が元の値の2倍であることが確認できるので、この結果を何かしらの解釈や分析に用いても問題ありません。
このように、比例尺度は計算のバリエーションが最も豊富なので、取得できる情報量も最も豊富であると言えます。
まとめ
ここまでは、データの種類2つと尺度4つについて、それぞれの特徴を確認してきました。最後に、各区分の特徴について図3でおさらいしておきましょう。
図で確認してみると、扱いの自由度と取得できる情報量が比例尺度、間隔尺度、順序尺度、名義尺度の順になっていることが一目瞭然です。
関連記事
 数学ができると「数学ができないエンジニアはダメだ」の効果が計れる
数学ができると「数学ができないエンジニアはダメだ」の効果が計れる
数学ができるとエンジニアとして活躍できるのか、むしろ数学ができないとエンジニア失格なのか?――「エンジニアに数学の知識は必要か?」を、数学オタクが論理的に解説します。 Pythonの文法、基礎の基礎
Pythonの文法、基礎の基礎
今回は、Pythonの制御構造と、リスト/タプル/辞書/集合という4つのデータ型について超速で見ていく。 Pythonで機械学習/Deep Learningを始めるなら知っておきたいライブラリ/ツール7選
Pythonで機械学習/Deep Learningを始めるなら知っておきたいライブラリ/ツール7選
最近流行の機械学習/Deep Learningを試してみたいという人のために、Pythonを使った機械学習について主要なライブラリ/ツールの使い方を中心に解説する連載。初回は、筆者が実業務で有用としているライブラリ/ツールを7つ紹介します。
Copyright © ITmedia, Inc. All Rights Reserved.

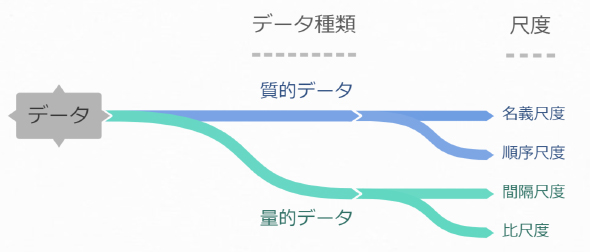 図1 データの種類の概形
図1 データの種類の概形