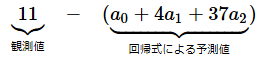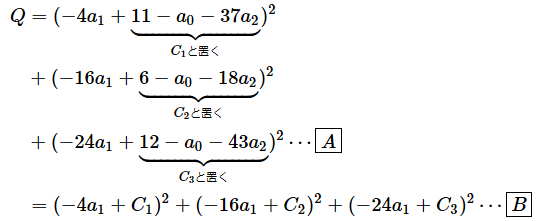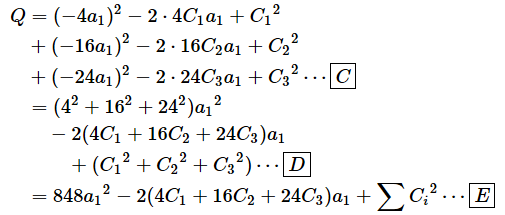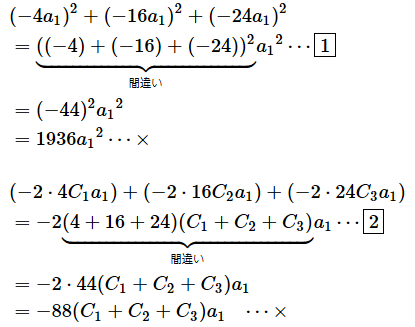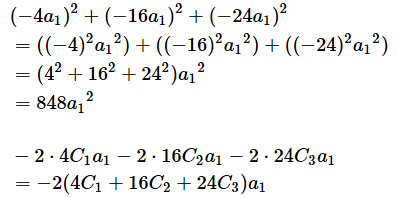［AI・機械学習の数学］偏微分を応用して、重回帰分析の基本を理解する：AI・機械学習の数学入門（1/2 ページ）

これまでに見てきた、説明変数が1つだけの回帰分析と偏微分の基本知識を踏まえて、複数の説明変数がある重回帰分析を行うための基本的な方法を理解しよう。

[羽山博，著]

連載目次

　前々回は「説明変数が1つだけの回帰分析」を、前回は偏微分の考え方と計算の方法について学びました。それらの内容を踏まえて、今回は偏微分の応用編として「説明変数が複数ある重回帰分析」を行う方法を見ていきます。

目標： 偏微分を利用して重回帰分析を行う

　重回帰分析の回帰式の例は以下のようなものでした。いくつかの値を基に、このような回帰式の定数項と係数を求めようというのがここでの目標です。

　回帰式の求め方は前々回の例と同様で、観測値（実際に得られたデータ）と理論値（回帰式で求めた値）との差の二乗和が最小になるように定数項や係数を決めるという方法です。

解説：偏微分を利用して重回帰分析を行う

　まずは、具体的な例で考えてみましょう。図1のような不動産データがあったとします。このデータを基に回帰式の定数項と係数を求めてみたいと思います。実はこの例であればExcelでもできるので、ついでにExcelで回帰式を求めた結果も示してあります。

図1　不動産データと重回帰分析の例

　［A］列から［D］列のデータが不動産データです。このデータを基に回帰式を求めた結果が［F］列から［D］列になります。ちょっと注意しないといけないのは、係数の順序が元のデータと異なるということです。回帰式は、以下のようになります。

　築年数が大きくなるとやや家賃が下がり、面積が大きくなると家賃が上がるということが分かりますね。定数項は面積も築年数も0の物件の家賃ということになるので、違和感があるかもしれませんが、不動産業務のための固定費と考えてもいいでしょう（前々回の「説明変数が1つだけの回帰分析」では、そういう場合は0としました）。

　家賃をy、築年数をx₁、面積をx₂とすると、以下のように表せます。1.9292は定数項ですね。

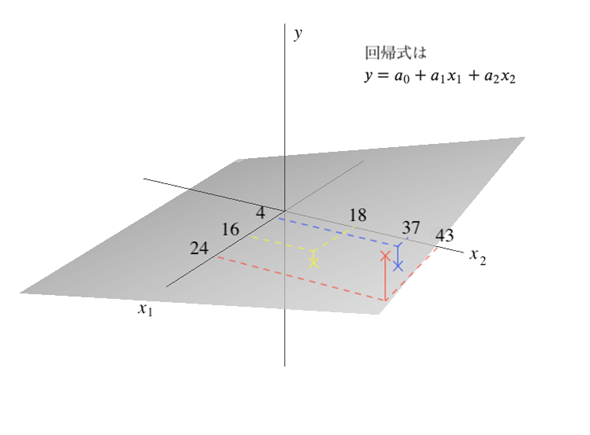
　説明変数が2つあるので、図にするとちょっと見づらいですが、図2のようなイメージです。回帰式は直線ではなく平面を表します。誤差がプラスになるのかマイナスになるのかはこの時点では分からないので、とりあえずイメージだけつかんでおいてもらうといいでしょう*1。

*1　平均や分散などを求めるときには、実際の測定値と推定値（理論値）との差を「誤差」と呼びますが、回帰分析などでは、実際の測定値と予測値（理論値）の差のことを「残差」と呼ぶのが一般的です。以降、測定値と回帰式で求めた値の差を「残差」と呼ぶことにします。例えば、そのような差の二乗和は、誤差二乗和ではなく「残差二乗和」（あるいは「残差平方和」）と呼びます。ちなみに、統計学の回帰分析とは異なり、機械学習のニューラルネットワークでは、正解値（学習用に正解としてラベル付けされた値）と推定値（理論値）との差を「誤差」と呼び、その差の二乗和を2で割ったものを「二乗和誤差」と呼ぶのが一般的なので、統計学の用語と機械学習の用語で混同しないよう注意しましょう。

図2　回帰式で表される平面の例

　この時点では、まだ定数項や係数は分からない（これから求める）ので、回帰式は以下のようになります。

残差二乗和を求める

　私たちがやりたいことは、築年数と面積の各点の最も近くを通る回帰式（平面の式）を求めるということです。そこで、各データと回帰式で求めた値の差（残差）をそれぞれ求めてみましょう。ここからの説明については動画も用意してあります。ちょっと難しいな、と感じたらぜひ視聴してみてください。

動画1　残差平方和の算出

　1件目のデータは、x₁（築年数）が4、x₂（面積）が37、y（家賃）が11なので、残差は、

となります。同様に、2件目のデータと3件目のデータの残差も以下のようになります。

　回帰式を求めるためには最小二乗法を利用します。前々回も説明しましたが、再度、説明すると、最小二乗法というのは、これらの残差の二乗の総和（残差二乗和）が最小になるように、定数項（a₀）や係数（a₁、a₂）の値を決めるということでしたね。

　では、上記の残差を全て二乗して足してみましょう。どのような式になるでしょうか。確認しながら見ていくために穴埋めにしておきましょう。オレンジ色の部分をクリックまたはタップすると答えが表示できます。なお、いちいち残差二乗和と呼ぶのが面倒なので、残差二乗和をQと表すことにします（特にQという文字に意味はありません）。

　　Q ＝ (11 − (a₀ ＋ 　4　a₁ ＋ 　37　a₂))　²　
　　　　＋ (6 − (a₀ ＋ 16a₁ ＋ 　18　a₂))　²　
　　　　＋ (12 − (a₀ ＋ 　24　a₁ ＋ 43a₂))　²　

　何だかものすごく複雑な式になっているように見えますが、このQ式を最小にするa₀、a₁、a₂を求めるということなので、まずはa₀で偏微分するとよさそうです。次にa₁で偏微分、最後にa₂で偏微分するというわけですね。しかし、ここでは、あえてa₁での偏微分を先にやることにします。別にa₀から順にやってもいいのですが、a₁での偏微分の方が、式の特徴がよく分かるという、ただそれだけの理由です。

　a₁で偏微分するということは、他の変数は定数として扱えるというわけですから、a₁で整理し、他の変数や定数を全て定数にしてみましょう。

［A］ ⋯ a0について整理した（項の順序を変えただけ）
［B］ ⋯ a0以外の部分をC₁、C₂、C₃と置いた

　例えば、C₁＝ 11 − a₀ ＋ 37a₂と置くといった具合です。これらは定数として扱うといっても、同じ値ではないので全て同じCにしてはいけません。そこで、C₁、C₂、C₃と置いたわけです。

　さらに［B］式を展開していきましょう。二乗の展開公式を使ってかっこを展開し、a₁の降べきの順に並べます*2。

［C］ ⋯ 二乗の展開公式を使ってかっこを展開した
［D］ ⋯ a1の降べきの順に並べた。(−a₁)²＝a₁²なのでマイナスを取った
［E］ ⋯ C₁＋C₂＋C₃をΣC_iのように表した。

*2　［C］式から［D］式への変形では、次のような計算間違いをしやすいので注意してください。実は、全て文字を使ったりΣなどの記号を使ったりすると間違えにくいのですが、具体的な数字を使って計算する場合には、筆者もうっかりと、しでかしてしまうことがあります。文字や記号を使う意味はそういうところにもあるわけですね。

［1］式では二乗してから足す必要があるのに、足してから二乗しています。
［2］式では各項に掛けてから足す必要があるのに、足してから各項に掛けています。C₁、C₂、C₃が異なるものであることに注意しましょう（同じものであれば単純にくくり出せます）。

　正しい計算は以下の通りです。

次のページは……

　では、いよいよ、次のページでQをa₁で偏微分してみましょう。