[AI・機械学習の数学]偏微分の基本(意味と計算方法)を理解する:AI・機械学習の数学入門
「偏微分」って何? いかにも難しそうな名前だが、微分を理解していれば意外に簡単。前回までの知識を踏まえて、今回は偏微分の意味と計算方法を理解しよう。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
微分は関数が最小値を取るときのxの値を求めるために使えます。前回はその具体的な利用例として、最小二乗法による回帰分析を行う方法を紹介しました。しかし、取り扱った回帰式はy=axという単純なものだけでした。そこで「偏微分」を利用し、複数の説明変数があるときにも最小二乗法が使えるようにします。つまり、重回帰分析の方法を見ていこうというわけです。
そのために今回は、偏微分の考え方と計算の方法について簡単な例で見ておくことから始めます。続けて次回、偏微分を利用して重回帰分析を行う方法を紹介します。
目標: 偏微分の意味と計算方法を理解する
複数の変数があるような関数(多変数関数)を微分するときに、1つの変数にだけ注目し、それ以外は定数として扱うというのが偏微分です。簡単な例を示しておきます。
のとき、
- xで偏微分すると以下のようになります。
- yで偏微分すると以下のようになります。
偏微分は高校の数学では学びませんが、微分の延長線上にある話なのでさほど難しくはありません。「∂」という変わった記号を使うので抵抗を感じる人もいますが、話を聞けば「なーんだ、そんな簡単なものなのか」と思うはずです。では、「∂」の読み方と書き方から始めましょう。
解説:偏微分の意味と計算方法を理解する
偏微分のために使う「∂」という記号は、実は「d」を丸く書いたものです。「ラウンドディー」「デル」などと読みますが、文脈から偏微分であることが明らかな場合は、単に「ディー」と読むこともあります。書き方は図1の通りです。
小学生じゃあるまいし、筆順なんてどっちでもいいといえばそうなのですが、文字を見て覚えるだけでなく、一度手を動かして書いてみると、それだけでぐっと身近に感じられます。なお、たいていの日本語入力システムでは「でる」と入力して変換すれば「∂」が候補に表示されるはずです。
ところで、多変数関数というのはどのようなものなのでしょうか。これまでは、
の[A]のような説明変数(独立変数)が1つだけの1変数関数しか扱ってきませんでした。[A]の場合、式の右辺を見ると、
- xが変数
- aとbは係数
- cは定数項
であることが分かります。
多変数関数とは、
の[B]や[C]のような関数です。つまり、複数の説明変数がある関数だというわけです。[B]では、
- xとyが変数
- a,b,cは係数
- dは定数項
ですね。[C]では、
- x1, x2, ⋯ xnが変数
- a1, a2, ⋯ anは係数
- a0は定数項
です*1。
*1 [B]のzや[C]のyも「変数」ですが、これらは「目的変数」(従属変数)と呼ばれるものでしたね。目的変数(左辺)は説明変数の値を決めれば自動的に値が決まるので、関数における変数の「個数」には数えません。以下、説明変数のことを単に「変数」と呼びます。
変数が3つ以上になると図で表すことは難しいのですが、変数が2つの場合は図2のような立体的なグラフになります。ただし、変数の次数や係数などにより、形はさまざまです。
偏微分の意味は「目標」のところで触れた通り、1つの変数にだけ注目し、それ以外は定数として扱うということです。図3のように、目的変数や関数名を上に書き、どの変数に注目するかを下に書きます。
読み方は「ラウンドディー・ゼット、ラウンドディー・エックス」のようになります(ちなみに、分数と同じ形をしていて、分数のように扱うこともできるので「ラウンドディー・エックス分のラウンドディー・ゼット」と読む人もいます)。これは、微分を以下のように表したときと同じですね。
もう少し例を示しておきましょう。
[A] ⋯
xとyの2変数関数fをxで偏微分する
[B] ⋯
関数fをxiで偏微分する
機械学習やディープラーニングでは、変数が多くなることが多いので、[B]のような書き方がよく使われます。また、以下のように「どの変数で微分するか」を小さく書いて表すこともあります。例えば、
のとき、f(x,y)をxで偏微分することを、
と表します。
というわけで、ここまでは「書き方」だけを見てきましたが、いよいよ、偏微分の計算方法を見ていくことにしましょう。例えば、
をxで偏微分してみます。以下の図4を見ながら、計算方法を確認してください。
xで偏微分するなら、まず、xの降べきの順、つまり次数の高い方から順に式を整理しておきます。次に、x以外の変数は「定数」と見なして微分します。上の例なら、y2+7y+5は定数と見なしました。つまり、3x2+4x+定数をxで微分する、ということになります。今までの微分の知識で計算できますね*2。
*2 「偏微分可能であるかどうか」ということも数学的には重要ですが、機械学習やディープラーニングでは、偏微分可能な関数をモデルとして扱うのが普通なので、ここでは触れないこととします。
念のため、偏微分の図形的な意味合いも確認しておきましょう。例えば、z=x2−3y2をxで偏微分するということは、yの値を固定してxで微分するということなので、z=x2−3y2で表されるグラフをy=y0(y0は何らかの決まった値)で切った断面のグラフを微分していると考えられます。
図5には分かりやすい例として、グラフを回転させy=0での断面が見えるようにしたものを示してあります。ちょうど馬の鞍(くら)のような形のものを、馬の頭からお尻の方向に切った感じのグラフになります。グラフを回転させて見やすくしたアニメーションも用意してあるので、参考にしてください。
このとき、この断面にあるグラフの式はz=x2になっていますね。偏微分とは、このような断面にあるグラフ(二次関数)で表されている式を微分するということです。厳密な証明は省きますが、yの値が異なっても微分すれば結果は同じです。例えば、y=2なら、z=x2−3y2はz=x2−12になりますが、微分すればやはりzx=2xです。
逆にxの値を固定してみましょう。図6はx=0での断面が見えるようにしたものです。こちらは、馬の鞍を輪切りにしたような感じのグラフです。
このとき、この断面にあるグラフの式はz=−3y2です。やはりxの値がいくらであっても、微分するとzy=−6yになります*3。
*3 全ての変数で同時に微分することを「全微分」と呼び、接平面の式を求める場合などに利用できます。が、ここでは詳細については触れません(いずれ機会があれば紹介したいと思います)。
偏微分という名前がいかにも難しそうですし、「∂」というへんてこな記号を使いますが、全然難しくなかったですね。ただ、計算ミスをする可能性もあるので、以下の練習問題で穴埋め問題を解きながら偏微分の計算方法を確認しておきましょう。オレンジ色の部分をクリックまたはタップすると答えが表示されます。(3)はこれまでのおさらいもかねた応用問題です。ちょっと手ごわいので、後回しにしても構いません。なお、練習問題の解答については動画を用意してあります。偏微分の計算方法に慣れるためにぜひ参照してみてください。
練習問題
動画2 偏微分に関する練習問題の解き方
(1)以下の関数をyで偏微分する手順を穴埋めで確認してみましょう
Copyright© Digital Advantage Corp. All Rights Reserved.

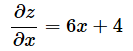
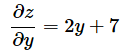
 図1 ∂の筆順
図1 ∂の筆順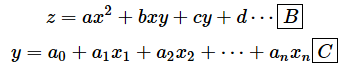

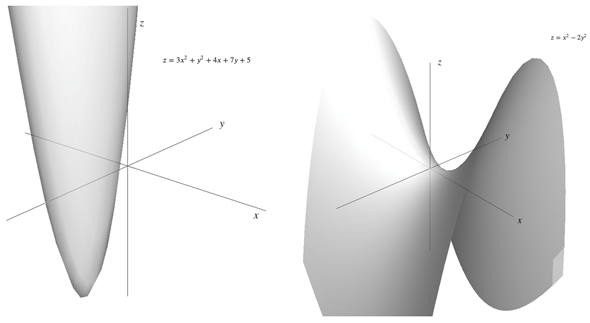
 図3 偏微分の書き方
図3 偏微分の書き方