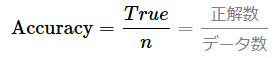第11回 機械学習の評価関数(二値分類/多クラス分類用)を理解しよう:TensorFlow 2+Keras(tf.keras)入門
分類問題で使える主要な評価関数をまとめ、使い分け指針を示す。具体的には二値分類用の「LogLoss」「AUC」「PR-AUC」を、さらに多クラス分類用の「正解率」「LogLoss」を説明する。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
前回は二値分類問題で使える基本的な評価関数を紹介した。
今回はそれを踏まえて、二値分類問題で使える応用的な評価関数と、多クラス分類用の評価関数をまとめる。具体的には下記の5個の評価関数を説明する。
評価関数については今回で最後となるので、ぜひ頑張って今回の分まで読み終えて、機械学習/ディープラーニングにおける代表的な評価関数を一通り押さえてほしい。本稿の最後では、TensorFlow/Keras(tf.keras)のcompile()&fit()メソッドを使った場合に「評価」を実行するための基本的な方法も紹介する。
二値分類用[応用編](Binary classification)
今回のLogLossとAUCは前々回と前回ほど評価関数の数式がシンプルではない。少し回り道になってしまうが、数式の意味をより深く理解するために、順序立ててグラフなどを示しながら説明していくのでお付き合いいただけるとうれしい。
LogLoss(Binary Logarithmic Loss)
前回は二値分類用の正解率を解説した。正解率の場合、モデルからの出力結果は(基本的に)陽性(Positive、正例、例えば犬)を意味する1、もしくは陰性(Negative、負例、例えば猫)を意味する0になる。例えば二値分類のモデルで、出力層の最後にあるシグモイド関数などの出力結果が0.7だった場合は、デフォルトでは0.5が閾値(しきい値)なので(基本的に)1(陽性)としてカウントし、0.3だった場合は(基本的に)0(陰性)としてカウントする。そうやってカウントしたものを、混同行列に当てはめることで正解率などが計算できる(※詳しくは前回を参照)。二値分類(例えば犬/猫の分類)をより正確に実現したい場合には、この正解率を活用するとよい。
しかし、陽性か陰性かという分類の正確さ(Accuracy)よりも、陽性もしくは陰性である確率の高さ(Probability)を評価スコアとして取得したい場合がある。例えば犬か猫かの分類ではきっちりとどちらかに分類してほしいが、病気の有無の分類ではそれよりも「病気である場合に、どれくらいの確率の高さで病気と分類されるか」の方が大切だろう。こういった場合には、正解率の代わりに、LogLoss(Binary Logarithmic Loss、二値分類用の対数損失)を使う方が適切である。
図1は、LogLossと正解率の違いをまとめたものだ。前述の通り、正解率(図1の右)はしきい値が(デフォルトでは)0.5になっているので、モデルからの出力結果が0.9でも0.5でも、予測値は陽性を意味する1と見なすが、この2つの出力結果にはかなり大きな差がある。0.5の判定は、あと少しで陰性を意味する0になってしまう微妙な値だ。このような微妙な値を出して、陽性か陰性を分類するモデルをあなたは信頼できるだろうか。もう少し厳密な確率値の高低で判定してほしいと思うはずだ。
一方のLogLoss(図1の左)にはしきい値がなく、モデルから出力された値(0.0〜1.0の、いわば100%確率値)をそのまま予測値として用いる。最終的な評価スコア(LogLoss/正解率)の算出は、全データに対する予測値と正解値を比較してその結果値の平均を取るわけだが、正解率が「1(陽性)か」「0(陰性)か」を分類する正確さが計算されるのに対し、LogLossでは、「1(陽性)」もしくは「0(陰性)」という正解にどれくらい近いか、逆にいうと正解からどれくらい乖離(かいり)しているかが算出される。
最終的な評価スコアとしてのLogLossは0.0(=近い)〜∞(=遠い)の範囲の値になり、数値が小さいほど「陽性の正解もしくは陰性の正解に近い」ことを意味するのでよりよい(※一方の正解率は「100%正確である」ことが一番なので、数値が大きいほどよりよい。つまり評価数値の大小関係が正解率とLogLossで真逆なので注意してほしい)。例えば先ほどのように予測値が0.5で正解値が1である場合、LogLoss値は0.693となり、あまり良くない数値となる。正解との乖離が大きくなるほどペナルティーも大きくなるというわけだ。
実はLogLossは、第3回や第8回でも登場した交差エントロピー誤差(Cross entropy error、「交差エントロピー損失:Cross entropy loss」や、単に「交差エントロピー:Cross entropy」とも呼ばれる)と同じものである。これまでの連載では説明を割愛していたが、LogLossの意味理解にもつながるので、あらためてここで詳しく説明しておこう。第3回では、回帰問題でよく使う損失関数が平均二乗誤差(MSE:Mean Squared Error)で、分類問題でよく使う損失関数が交差エントロピー誤差と説明した。その両者にどのような違いがあるかをまとめたのが図2である。
図2に示す2つのグラフを見比べてほしい。両グラフとも、横軸に予測値(p:0.0〜1.0の、いわば100%確率値)を、縦軸に評価スコア(それぞれの損失関数の出力値)を取っている。描画されている線の色が正解値(y:1=青色、0=オレンジ色)を意味する。なお、グラフの下にはグラフに対応する数値表も付けておいた。
回帰問題に使う平均二乗誤差(図2の右)の値(=青色の線/オレンジ色の線における縦軸の値、つまり評価スコア)は、0.0〜1.0の範囲で緩やかに変化している。それに対し、分類問題に使う交差エントロピー誤差(図2の左)の値は0.0〜∞(無限大)の範囲で急激に変化している。0.0から離れれば離れるほど非常に悪い数値となっていくわけである。例えば予測値が1.0で正解値が1である場合(赤色の丸で示した部分では)、両者の近さはゼロなので、LogLoss値(評価スコア)は0.0となる。一方、例えば予測値が0.0で正解値が1である場合(紫色の丸で示した部分では)、両者は最も遠いので、LogLoss値は∞となる(※正解値の場合は1.0なので大きな違いである)。
つまり分類問題はこのように指数関数的に変化する方がくっきりと分かれて違いを付けやすいということである。「指数関数」と書いたが、その親戚である自然対数(Natural logarithm: ネイピア数eを底とする対数)を使うと、微分などが行いやすくなって数学的に便利だ。ただし図3の左に示すように、自然対数では入力が0.0〜1.0の部分における出力は-∞〜0.0というマイナス領域となっており、そのままでは使えない。そこで自然対数にマイナスを掛けてプラスに転じさせて使う。具体的には−自然対数(p)という式になる。図3の右に示すグラフがそれで、このグラフが図2の交差エントロピー誤差の青色の線(y=1: 正解が「1:陽性」である場合)と一致しているのが分かるだろう。
前掲の図2の交差エントロピー誤差にはオレンジ色の線(y=0)もある。この出力を行うには、0.0〜1.0という予測値(p)を反転させる、つまり1−pをすればよい。具体的には−自然対数(1−p)という式になる。この式は正解値が陰性(y=0: 正解が「0」であるデータ)のときだけ有効にして、正解値が陽性(y=1: 正解が「1」であるデータ)のときには無効にしたいので、−自然対数(1−p)に(1−y)(=陽性のときは0、陰性のときは1)を掛けることで無効/有効を制御する。先ほど青色の線を示す−自然対数(p)の前にも同様に(y)(=陽性のときは1、陰性のときは0)を掛けることで有効/無効を制御する。この2つの式を足し合わせた下記の式が、個々のデータに対するLogLoss(=交差エントロピー誤差)の計算式そのものである(※式の左半分が青色の線、右半分がオレンジ色の線に該当する)。
最終的なデータ全体のLogLoss値(評価関数の場合。損失関数の場合は交差エントロピー誤差)を算出するには、上記で計算した個々のデータに対するLogLoss値の平均値、つまり全部足し合わせてデータ数(n)で割る計算をすればよい。その式は次の通りだ。マイナス(−)は総和(Σ)の前にくくり出していることに注意してほしい。
以上、遠回りになったが、LogLossの計算式と意味を押さえた。ちなみに上記の式は、情報理論における「交差エントロピー」(Cross Entropy)と呼ばれる尺度で得られる式と同じである。
ちなみにTensorFlow/KerasでのLogLoss/交差エントロピー誤差の計算には、
を使えばよい。ただし、二値分類の損失関数には'binary_crossentropy'文字列/tf.keras.losses.BinaryCrossentropyクラスを指定することが多いが、その場合、その損失(loss)値がそのままLogLossであるため、さらにメトリクスとしてtf.keras.metrics.BinaryCrossentropyクラスを指定する必要はない。
このようなLogLossだが、正解率よりも汎用(はんよう)的に使えるので、特にビジネス領域では広く活用されている。先ほどは病気の有無の二値分類を例として出したが、他には例えばWebサイトのバナー広告が「クリックされる/されない」の二値分類も、やはり確率値をそのまま使うLogLossの方が正解率よりも適しているだろう。このように、正解率よりもLogLossの方が適した場面は実ビジネスで多い。
万能に見えるLogLossだが欠点もある。LogLossは個々のデータが正解からどれくらい近いかを算出して平均するので、データセットが違うと、当然ながらLogLossの結果も変わってくる。つまり、異なるデータセットを使って機械学習モデルをLogLossにより比較することはできない。比較したいのであれば、同一のテストデータを用いる必要がある。重要な点なので忘れないように注意してほしい。このようなモデル間の比較を行いたい場合は、次に説明するAUCの方が適切である。
AUC(Area Under the ROC Curve)
前節のLogLossの最後に述べたように、機械学習モデルの性能を比較するためなど、モデルの精度(=性能:performance)をより汎用的に計測したい場合には、AUC(Area Under Curve)という評価指標を用いるのが適切である。
また、正解率よりも優れている利点としては、AUCはしきい値の影響を受けないことが挙げられる。正解率は、デフォルトで0.5をしきい値として、予測値は0.5以上なら1、0.5未満なら0という形で評価値が決まる。このしきい値は変えることもできるが、その場合、評価値も変わってしまうという問題がある。こうなるとやはりモデルの性能比較が行えないので、しきい値の影響を受けずにより汎用的なモデル性能が計測できるAUCの方が正解率よりも適切である。
例えば貸金業で貸し倒れリスクを予測する、つまり「貸し倒れる/貸し倒れない」という二値分類を行うモデルであれば、「厳しく判定したい」「緩く判定したい」といった形で利用目的に応じてしきい値を変更することが考えられるだろう。この場合、しきい値の影響を考慮せずに、汎用的なモデルの精度の良さを計測したい。こういった場面では、正解率でもLogLossでもなく、AUCを使った方がよい。
AUCには主に、
- 通常の、ROC曲線(後述)を使ったAUC(本節で解説)
- PR曲線を使ったAUC(次節で解説)
の2種類がある。
単にAUCと書かれている場合、通常はROC曲線の下にある領域(Area Under the ROC Curve、これを略して「AUC」)を意味する。ROC曲線(Receiver Operating Characteristic curve:受信者操作特性曲線)とは、
- 縦軸(y軸)に真陽性率(True Positive Rate:TPR)(詳細後述)
- 横軸(x軸)に偽陽性率(False Positive Rate:FPR)(詳細後述)
を取った曲線で、例えば図4のようなグラフとなる。
このROC曲線(図4の青色の線)の下にある領域(図4の水色の領域)の面積がAUCの値となる。横軸も縦軸も0.0〜1.0の範囲なので、その面積は0.0×0.0=0.0〜1.0×1.0=1.0、つまり最小値が0.0で、最大値は1.0となる。AUCは1.0に近いほどよい。AUCが1.0になるのは、図4でオレンジ色の線で示した「理想的な曲線(ideal curve)」の場合である(図4の薄黄色+水色の領域の面積が1.0)。ランダムに推測(random guess)するモデルだと、基本的にAUCは0.5となる。参考までにAUC値の基準を挙げると次のようになる。
- 0.9〜1.0: 非常によい(excellent)
- 0.8〜0.9: よい(good)
- 0.7〜0.8: まあまあ(fair)
- 0.6〜0.7: よくない(poor)
- 0.5〜0.6: 失敗(fail)
では、このROC曲線をどうやって描くかだが、まずは真陽性率(True Positive Rate)と偽陽性率(False Positive Rate)の計算式を押さえよう。計算式にあるTP/TN/FP/FNは前回説明したが、復習として図5に混同行列と計算式の関係を図示した。
この計算式を見て気付いたかもしれないが、真陽性率は感度(Sensitivity)/再現率(Recall)と全く同じ式である。偽陽性率は「1から特異度(Specificity)を引いた式」と同じ意味である。
感度や特異度では分類判定のしきい値を指定したが、AUCの真陽性率&偽陽性率では0.0〜1.0の範囲でしきい値(threshold value=カットオフポイント:cutoff points)を細かく指定していく。tf.keras(TensorFlow/Keras)のtf.keras.metrics.AUCクラスではデフォルトでnum_thresholds=200となっており、0.0〜1.0の範囲で200個の(例えば1.0、0.095、0.09、0.085……のように)しきい値を指定して、真陽性率と偽陽性率を同時に求める。ちなみにライブラリ「scikit-learn」のsklearn.metrics.roc_curve()関数では最適なしきい値を自動的に指定する仕様になっており、基本的にKerasと同じAUC値にはならないので注意してほしい。
まずは、例えばしきい値1.0の真陽性率(y)と偽陽性率(x)を計算し、(x,y)座標に点をプロットする。同様にしきい値を0.095、0.09、0.085……とずらしながら点をプロットして(※大きい方から小さい方にずらしたが、もちろん小さい方から大きい方にずらしてもよい)、最終的にそれらの点を直線でつないだものがROC曲線である(図6)。しきい値が大きい間(例えば0.095)は、ほとんどの予測値が陰性となるため、陽性予測の正解(TP:True Positive)と陽性予測の不正解(FP:False Postive)は少ないが、しきい値を小さくするたびに陽性予測の正解(TP)と陽性予測の不正解(FP)は増えていく。しきい値が完全に小さくなると(例えば0.0)、全ての予測値は陽性となるため、陽性予測の正解(TP)と陽性予測の不正解(FP)はともに最大(全て)となる。このような流れで、徐々に右肩上がりの曲線になるわけである。
なお図6のROC関数は、ガタガタとした曲線になっているが、これが本来の姿で、データ数を意図的に絞って描画したためである。データ数が多くなると、前掲の図4に示したようにあたかも滑らかの曲線のように見える。
AUCはROC曲線の下にある領域の面積を求めるが、通常、曲線の下の面積は数学の積分で求める。しかしAUCでは、台形法(trapezoidal rule:台形公式)という手法で定積分を近似計算することが一般的だ。台形法とは、図6にプロットした点から真下に向かって線を引いて、その線で囲まれた左の領域の面積を(小学校で学ぶ)台形の面積を求める公式(={上辺+下辺}×高さ÷2)を使って計算し、それらを足し合わせる方法だ。真下に引いた線が台形の下辺になり、その前に引いた線が上辺となる。各点を計算するたびに台形の面積を逐次計算していけば難なくAUCの値が算出できるはずだ。具体的な計算方法やコード内容の説明は割愛するが、この説明が分からなくても、実際の計算はライブラリ任せになるので問題はない。
AUCはこれまでのように1つの式では表現できないので、このような文章での説明となった。以上でAUCの計算式と意味を押さえた。
TensorFlow/KerasでのAUCの計算には、
を使えばよい。
このようなAUCだが、やはり欠点がある。AUCの真陽性率は正解値が陽性のものだけを対象にした値で、偽陽性率は正解値が陰性のものだけを対象にした値である。よって、正解値が陽性であるデータの数と、正解値が陰性であるデータの数が極端に不均衡(imbalanced data)な場合、その影響をもろに受けてしまう可能性がある。例えば正解値が陽性のデータ数が少なすぎる場合、真陽性率が偽陽性率よりも個々のデータに敏感に反応するようになり、図4のようなきれいなグラフにならない可能性が高まる。よってROC曲線を使ったAUCを評価指標として用いる場合には、教師ラベルの陽性と陰性はできるだけ同じくらいの数にそろえた方がよい。それができない場合は、次に説明するPR曲線を使ったAUCを使うことを検討するとよい。
PR-AUC(Area Under the Precision-Recall Curve、AUC-PR)/AP(Average Precision)
本節では、前節のAUCの解説を踏まえて、そこからの違いや差分を中心に説明していく。
前節のAUCの最後に述べたように、不均衡なデータ(imbalanced data)の場合は、ROC曲線ではなくPR曲線(後述)という別の切り口の曲線を使ったAUC(Area Under Curve)を評価指標として用いるとよい。不均衡なデータの例としては、例えば「メールがスパムかどうか」という二値分類などが考えられる。スパムメール(陽性)の数が通常のメール(陰性)よりも極端に少ない、つまり不均衡なデータである場合は、その評価指標としてROC曲線のAUCは向いていない可能性がある。このような場合に、PR曲線のAUCを使うとよい。
PR曲線のAUCとは、PR曲線の下にある領域(Area Under the Precision-Recall Curve、これを略して「PR-AUC」もしくは「AUC-PR」、別名「AP:Average Precision」)を意味する。PR曲線(Precision-Recall curve:適合率-再現率の曲線)とは、
- 縦軸(y軸)に適合率(Precision)(詳細後述)
- 横軸(x軸)に再現率(Recall)(詳細後述)
を取った曲線で、例えば図7のようなグラフとなる。
ROC曲線がPR曲線に変わってグラフが右肩上がりから右肩下がりになっただけで、AUC値の範囲や意味は基本的に同じである。ROC曲線では、ランダムに推測(random guess)すると、基本的にAUCは0.5となった。しかしPR曲線では、ランダムに予測しても、AUCが0.5になるとは限らず、陽性と陰性のデータ数の割合によって数値が変わる。よってPR-AUCは、ROC曲線のAUCと比べて「モデルの汎用的な精度の測定や比較という用途にはあまり向いていない」ともいえる。正解率と比べて「しきい値の影響を受けない」というメリットはROC曲線のAUCと同じである。
このPR曲線をどうやって描くかだが、まずは適合率(Precision)と再現率(Recall)の計算式を押さえよう。いずれの計算式も前回説明済みだが、復習として図8に混同行列と計算式の関係を図示した。
お気づきの通り、再現率は先ほどの真陽性率と全く同じ式である。ただしROC関数では縦軸(y軸)に用いたが、PR関数では横軸(x軸)に用いる点が異なる。
まず、例えばしきい値0.0の適合率(y)と再現率(x)を計算し、(x,y)座標に点をプロットする。同様にしきい値を0.005、0.01、0.015……と(先ほどのROC曲線の説明とは逆順に)ずらしながら点をプロットして、最終的にそれらの点を直線でつないだものがPR曲線である(図9)。しきい値が小さい間(例えば0.005)は、ほとんどの予測値が陽性となるため、陽性予測の正解(TP:True Positive)は多いが、しきい値を大きくするたびに陽性予測の正解(TP)は減っていく。しきい値が完全に大きくなると(例えば1.0)、全ての予測値は陰性となるため、陽性予測の正解(TP)は最小となる。このような流れで、徐々に右肩下がりの曲線になるわけである。
なお図9のPR関数も(先ほどのROC関数と同様に)、ガタガタとした曲線になっているが、これが本来の姿で、データ数を意図的に絞って描画したためである。データ数が多くなると、前掲の図7に示したようにあたかも滑らかの曲線のように見える。
ちなみに前回の「図5 適合率と再現率のトレードオフ」でも示したように、そもそも適合率と再現率はトレードオフ関係にあり、再現率(x軸)の数値が大きくなるにつれて、適合率(y軸)は小さくなる。これが図9のグラフにも表れている。
PR曲線の下にある領域の面積を求める方法は、ROC曲線のAUCと同じである。
PR-AUCも1つの式では表現できないので、このような文章での説明となった。以上でPR-AUCの計算式と意味を押さえた。
TensorFlow/KerasでのPR-AUCの計算には、ROC関数のAUCと同様に、
を使えばよい。AUCクラスのコンストラクター(__init__()関数)の引数curveに'PR'を指定することで、PR-AUCモードとなる。
多クラス分類用(Multi-class classification)
正解率(Multi-class Accuracy)
多クラス分類用の正解率(Multi-class Accuracy)は、二値分類用の正解率(Binary Accuracy)を多クラスに拡張したものである。よって、ここではポイントを絞って簡単に説明する。
二値分類では、1つの数値を共有して端(0.0)から端(1.0)を双方向に使い分けることで、
- 陽性(Positive、正例、例えば犬): 0.0(不正解)〜1.0(正解)
- 陰性(Negative、負例、例えば猫): 1.0(不正解)〜0.0(正解)
という2つのクラスを定義していた。ここでは多クラス分類の簡単な例として、クラス数を1つ増やして、
- クラス1「犬(Dog)」: 0.0(不正解)〜1.0(正解)
- クラス2「猫(Cat)」: 0.0(不正解)〜1.0(正解)
- クラス3「狐(Fox)」: 0.0(不正解)〜1.0(正解)
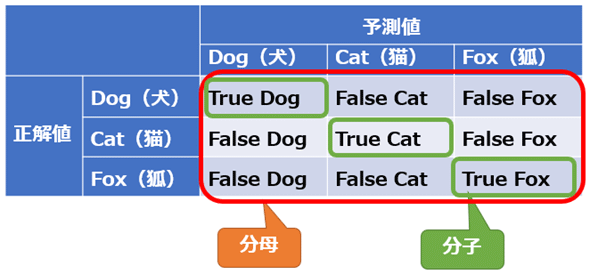
という3つのクラスを定義してみることにしよう。これを二値分類の混同行列のように3行3列のクロス表にすると図10のようになる。
二値分類の場合と考え方は同じで、機械学習モデルによる予測における正解数をデータ数で割った値が正解率である。0.0(=0%)〜1.0(=100%)の範囲の値になり、1.0に近づくほどよりよい。
なお、二値分類では正解率の計算式を混同行列のTP/TN/FP/FNを使っても表現したが、多クラス分類では陽性(P)/陰性(N)ではなく、3つ以上のクラスなのでTPなどという用語では表現できないことに注意してほしい。
TensorFlow/Kerasで多クラス分類用の正解率を計算するには、正解ラベルが数値エンコーディング(※第8回で解説済み)されたスパースラベル(=クラスインデックス)の場合は、
を、正解ラベルがone-hotエンコーディングされている場合は、
を使えばよい。もしくは(compile()メソッドの引数metricsで)、
- 'accuracy'
- 'acc'
という文字列を使えばよい。ちなみに筆者が試した限りでは'sparse_categorical_accuracy'という文字列は使用できなかった。
LogLoss(Multi-class Logarthimic Loss)
多クラス分類用のLogLoss(Multi-class Logarthimic Loss)は、二値分類用のLogLossを多クラスに拡張したものである。よって、ここではポイントを絞って簡単に説明する。
二値分類の場合と考え方は同じで、機械学習モデルによる予測が正解にどれくらい近いか、逆にいうと正解からどれくらい乖離しているかを表す値がLogLossである。0.0〜∞(無限大)の範囲の値になり、0.0に近づくほどよりよい。
先ほどの正解率と同じ説明の繰り返しになってしまうが、二値分類では、1つの数値を共有して端(0.0)から端(1.0)を双方向に使い分けることで、
- 陽性(Positive、正例、例えば犬): 0.0(不正解)〜1.0(正解)
- 陰性(Negative、負例、例えば猫): 1.0(不正解)〜0.0(正解)
という2つのクラスを表現していた。これにより各データのLogLoss(交差エントロピー誤差)値は、正解値をy、予測値をpと置くと、「陽性が正解」用の−y自然対数(p)と、「陰性が正解」用の−(1−y)自然対数(1−p)という2つの式を組み合わせた計算で取得することができた。
一方、多クラス分類では、1つの数値を共有するわけではなく、クラス数分の数値を用いる。例えば、
- クラス1「犬(Dog)」: 0.0(不正解)〜1.0(正解)
- クラス2「猫(Cat)」: 0.0(不正解)〜1.0(正解)
- クラス3「狐(Fox)」: 0.0(不正解)〜1.0(正解)
という3つのクラスを定義した場合、クラス1が正解用の−y1 自然対数(p1)と、クラス2が正解用の−y2 自然対数(p2)と、クラス3が正解用の−y3 自然対数(p3)という全く同じ式を組み合わせることになる。総和記号を使ってまとめると次の数式が定義できる。マイナス(−)は共通するので総和(Σ)の前にくくり出していることに注意してほしい。mはクラス数を表すので、先ほどの例だとm=3となる。
最終的なLogLoss値を算出するには、上記で計算した個々のデータに対するLogLoss値の平均値、つまり全部足し合わせてデータ数(n)で割る計算をすればよい。その式は次の通りだ。
TensorFlow/Kerasで多クラス分類用のLogLoss/交差エントロピー誤差を計算するには、正解ラベルが数値エンコーディングされたスパースラベル(=クラスインデックス)の場合は、
を、正解ラベルがone-hotエンコーディングされている場合は、
を使えばよい。ただし、多クラス分類の損失関数には'sparse_categorical_crossentropy'文字列/tf.keras.losses.SparseCategoricalCrossentropyクラスもしくは'categorical_crossentropy'文字列/tf.keras.losses.CategoricalCrossentropyクラスを指定することが多いが、その場合、その損失(loss)値がそのままLogLossであるため、さらにメトリクスとしてtf.keras.metrics.SparseCategoricalCrossentropyクラスなどを指定する必要はない。
compile()&fit()メソッド使用時に「評価」を実行する方法
本連載の中で評価を実行する方法をまだ説明していない。第9回〜第11回に紹介したクラスや関数を使えば算出できるが、compile()&fit()メソッドを使ってモデルをトレーニングした場合にはより手軽に評価値を取得できるので、評価関数の関連事項として本稿の最後に紹介させてほしい。ちなみに、初中級者向けの書き方であるcompile()&fit()メソッドではなく、エキスパート向け書き方であるtf.GradientTapeクラスを使ってトレーニングした場合(=カスタムの学習方法の場合、第5回を参照)は、各評価関数のクラスや関数を使って算出すればよい。
先にコードを示すとリスト1のようになる。太字部分が評価を実行するためのコードである。
import tensorflow as tf
# ……基本的なコードなので省略……
# モデル(NeuralNetworkクラス)のインスタンス化
model = NeuralNetwork()
# 定数(学習方法設計時に必要となる数値)
LOSS = 'binary_crossentropy' # 損失関数:二値分類用の交差エントロピー
# 評価関数の定義:二値分類用の正解率、LogLoss、AUC、PR-AUC
METRICS = ['binary_accuracy'
,tf.keras.metrics.BinaryCrossentropy()
,tf.keras.metrics.AUC(num_thresholds=200, curve='ROC', name='AUC')
,tf.keras.metrics.AUC(num_thresholds=200, curve='PR', name='PR-AUC')]
OPTIMIZER = tf.keras.optimizers.Adam # 最適化:Adam
LEARNING_RATE = 0.001 # 学習率: 0.001(学習率の調整)
# 学習方法を定義する
model.compile(optimizer=OPTIMIZER(learning_rate=LEARNING_RATE),
loss=LOSS,
metrics=METRICS) # 評価指標の指定
# 定数(ミニバッチ学習時に必要となるもの)
BATCH_SIZE = 96 # バッチサイズ: 96
EPOCHS = 100 # エポック数: 100
# 学習(トレーニング)する
hist = model.fit(x=X_train, # 訓練用データ
y=y_train, # 訓練用ラベル
validation_split=0.2, # 精度検証用の割合:20%
batch_size=BATCH_SIZE, # バッチサイズ
epochs=EPOCHS, # エポック数
verbose=1) # 実行状況表示
# 評価する
loss, accuracy, logloss, auc, pr_auc = model.evaluate(X_test, y_test, verbose=1)
# 63/63 [==============================] - 0s 3ms/step - loss: 0.5821 - binary_accuracy: 0.8730 - binary_crossentropy: 0.5821 - AUC: 0.9302 - PR-AUC: 0.9270
print("二値分類用の正解率:", accuracy)
print("二値分類用のLogLoss:", logloss)
print("↑損失関数の交差エントロピーと同じ:", loss)
print("AUC:", auc)
print("PR-AUC:", pr_auc)
# 出力例:
# 二値分類用の正解率: 0.8730000257492065
# 二値分類用のLogLoss: 0.5821197628974915
# ↑損失関数の交差エントロピーと同じ: 0.5821197628974915
# AUC: 0.9301785230636597
# PR-AUC: 0.9270078539848328
細かな説明は不要だと思うが、念のためポイントのみ解説しておこう。
まず、compile()メソッドのmetrics引数に評価関数を指定する。評価関数は、第9回〜第11回に紹介したクラスや関数、文字列などを指定すればよい。
次に、学習(トレーニング)が終わったらevaluate()メソッドを呼び出して評価関数を実行する。第1引数にテストデータ、第2引数にそのデータの正解ラベルを指定する。verbose=1引数は、処理実行中の状況を表示するためのオプションである。
evaluate()メソッドの戻り値では、損失関数の出力値とcompile()メソッドで指定した評価関数の出力値がリスト形式でまとめて返される。あとはこれを出力するなどして活用するだけである。
以上で、第9回〜第11回の全3回にわたり解説した評価関数は完結した。ここまで読んでいただいたことに感謝したい。
本連載で紹介した評価関数はあくまで代表的なものだけであり、他にも例えば多クラス分類用の評価指標であるF値(mean-F1/macro-F1/micro-F1)やQuadratic Weighted Kappaなど目的に応じてさまざまなものがある。世の中にある全ての評価関数を知ることは大変すぎるので、まずは本稿で紹介したものを理解して活用できれば問題ないだろう。もし知らない評価関数を使う必要性が発生したら、その都度、その評価関数を学ぶというスタンスをお勧めする。
評価関数を理解することは地味で面倒くさいことではあるが、活性化関数や損失関数と負けず劣らずに、むしろそれより重要で、必ず押さえるべき技術要素である(と筆者は考えている)。なぜなら、評価関数をよく理解していないと、機械学習モデルに対する正確な評価はできないと考えられるからだ。
しかしながら、評価関数を初心者でも理解できるように分かりやすく説明している資料は少ない(と筆者は感じている)。数式をまとめただけの情報はネット検索で多数見つかるが、その計算の中身や意味、用途が押さえられるようなまとまった情報は少ない。そこで第9回〜第11回の記事は、そういった点を意識して執筆したつもりである。読者諸氏の理解に少しでも役立っているとうれしい。なかなか一読では理解できないものもあると思うので、必要に応じて振り返る辞書のような使い方をしていただけるとさらにうれしい。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

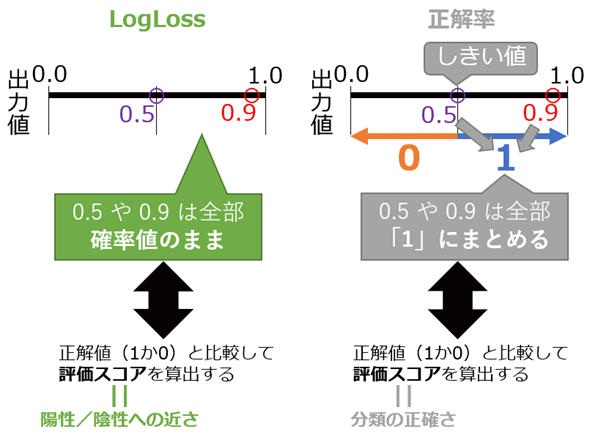
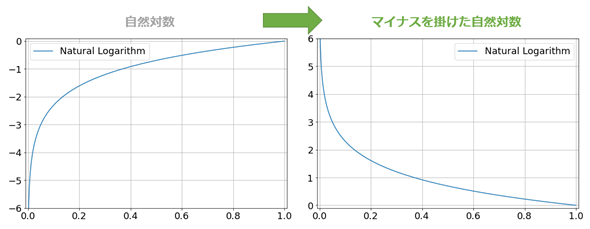

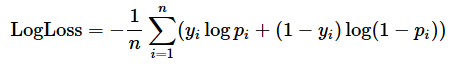
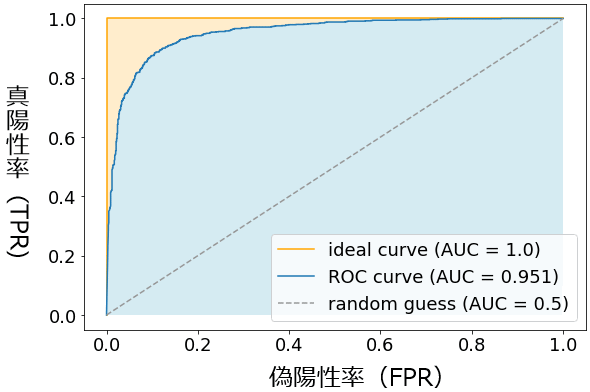 図4 AUCのグラフ例
図4 AUCのグラフ例
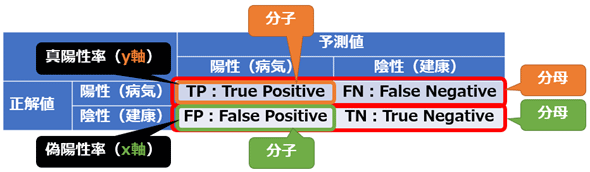
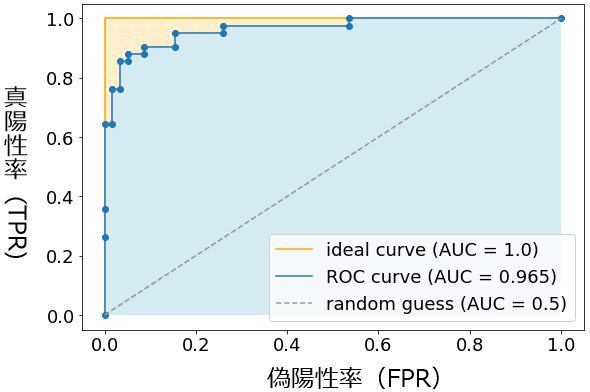 図6 ROC曲線のグラフ例
図6 ROC曲線のグラフ例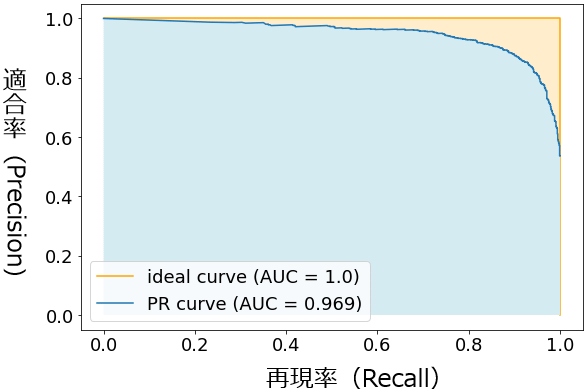 図7 PR-AUCのグラフ例
図7 PR-AUCのグラフ例
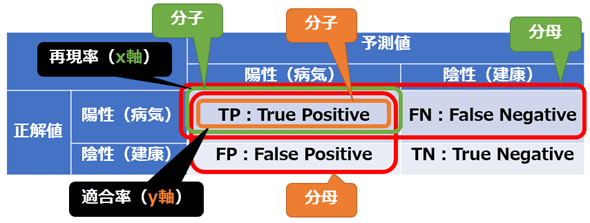
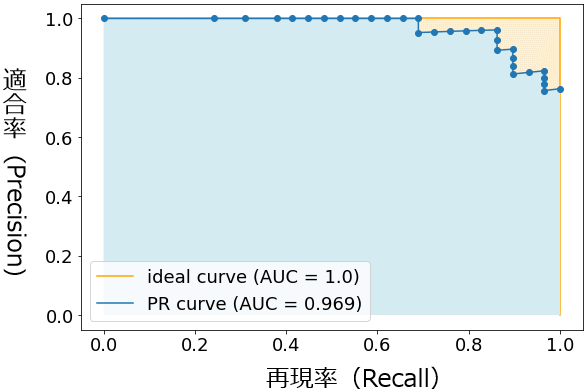 図9 PR曲線のグラフ例
図9 PR曲線のグラフ例