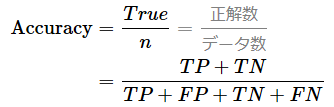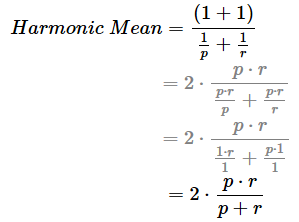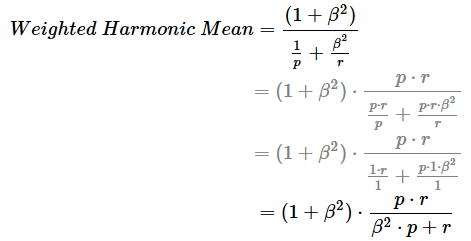第10回 機械学習の評価関数（二値分類用）の基礎を押さえよう：TensorFlow 2＋Keras（tf.keras）入門

二値分類問題で使える基礎的な評価関数をまとめ、使い分け指針を示す。具体的には正解率、適合率、再現率／感度、特異度、F値／F1スコア、重み付きF値／Fβスコアを説明する。

[一色政彦，デジタルアドバンテージ]

連載目次

　前々回は分類問題の解き方を解説した。その性能評価時における精度指標（Metrics）として正解率（Accuracy）を用いた。これは、最も基礎的で一般的な評価関数（Evaluation function）である。実践では、より多様な評価関数を使い分けることになるだろう。

　そこで今回は、二値分類問題で使える基本的な評価関数をまとめる（※前回は回帰問題の評価指標をまとめており、今回と次回はその続編である）。具体的には下記の6個の評価関数を説明する。

• 二値分類用［基本編］（Binary classification）
  • 正解率（Binary Accuracy）
  • 適合率（Precision）
  • 再現率（Recall）／感度（Sensitivity）
  • 特異度（Specificity）
  • F値（F-measure、F-score）／F1スコア（F1-score）
  • 重み付きF値（Weighted F-measure）／Fβスコア（Fβ-score）

　今回は二値分類用［基礎編］を説明するが、今回を踏まえて次回は、二値分類用［応用編］や多クラス分類用の評価関数について説明する。

• 次回前半「二値分類用［応用編］（Binary classification）」：
  • LogLoss（Binary Logarithmic Loss）
  • AUC（Area Under the ROC curve、ROC曲線のAUC）
  • PR-AUC（Area Under the Precision-Recall curve、AUC-PR）／AP（Average Precision）

• 次回後半「多クラス分類用（Multi-class classification）」：
  • 正解率（Multi-class Accuracy）
  • LogLoss（Multi-class Logarthimic Loss）

　では、早速1つずつ説明していこう。今回はこれまでの連載の中でも比較的難しめであるので、理解できない部分があれば時間をかけて何度も読むなどして頑張ってほしい。

二値分類用［基礎編］（Binary classification）

混同行列（Confusion Matrix）について

　二値分類の評価関数を理解するには、まずは混同行列（Confusion Matrix）を知っておく必要があるので、最初に説明させてほしい。簡単そうで間違いやすいところなので、冗長になるが例を使って丁寧に説明する。

　二値分類の問題に対する学習済みモデルの予測結果を評価して、正解率（何％正解か）を算出することを考えてみよう。二値分類の一方の値が例えば「YES（1.0）」で、もう一方が「NO（0.0）」であるとする（例えばタイタニック号乗客者の生存状況で生存がYES、死亡がNOなど）。予測値がYESのとき、正解値がYESなら正解（True）であり、正解値がNOなら不正解（False）である。また、予測値がNOのとき、正解値がNOなら正解（True）であり、正解値がYESなら不正解（False）である。二値分類ではこのように「二値分類の予測」×「正解と不正解」で4種類の組み合わせが考えられる。

　この4種類は性能を正確に評価するために明確に区別したい、というニーズがある。これに対応する定義が混同行列である。

• 予測値がYESで正解値がYESであれば、予測がYES（Positive：陽性）で正解（True：真）なので、これをTrue Positive（TP：真陽性）と呼ぶ
• 予測値がNOで正解値がNOであれば、予測がNO（Negative：陰性）で正解（True：真）なので、これをTrue Negative（TN：真陰性）と呼ぶ

　このように正解（True）時の予測値パターン（Positive／Negative）が2種類あるわけだ。同様に、不正解（False）時の予測値パターン（Positive／Negative）も2種類ある。

• 予測値がYESで正解値がNOであれば、予測がYES（Positive：陽性）で不正解（False：偽）なので、これをFalse Positive（FP：偽陽性）と呼ぶ
• 予測値がNOで正解値がYESであれば、予測がNO（Negative：陰性）で不正解（False：偽）なので、これをFalse Negative（FN：偽陰性）と呼ぶ

　もちろん二値分類はYES／NOだけではない。例えば犬／猫の二値分類なども考えられる。この場合、例えば犬が「YES（1.0）」、猫が「NO（0.0）」のように考えて混同行列を作ればよい。実際に「二値分類の予測」×「正解と不正解」で4種類の組み合わせを書き出すと下記の箇条書きのようになる（※ただしここでは、YESの予測は「陽性予測」、NOの予測は「陰性予測」と表現した。詳細後述）。

• 犬と予測して正解が犬ならTP（真陽性＝正解＆陽性予測）で
• 猫と予測して正解が猫ならTN（真陰性＝正解＆陰性予測）であり
• 犬と予測して正解が猫ならFP（偽陽性＝不正解＆陽性予測）で
• 猫と予測して正解が犬ならFN（偽陰性＝不正解＆陰性予測）である

　なお、先ほどまでは「YES／NO」と表現したが、一般的に「陽性（Positive）／陰性（Negative）」と表現するものと同じで、基本的に陽性（Positive）は「状態あり」、陰性（Negative）は「状態なし」を意味する。例えば病気への感染状態の有無（YES／NO）は「陽性／陰性」で表現することが一般的である。

　機械学習では、「陽性／陰性」ではなく、「正例（＝正に分類される事例）／負例（＝負に分類される事例）」と表現されることが多いので、「正例／負例」という呼び方は必ず知っておいてほしい。また「Positive／Negative」の文字通りに「肯定的／否定的」と表現されることもある。

　本稿では「陽性／陰性」という呼び方を採用することにした（※その理由は、「正例」と「正解」という漢字の見た目が紛らわしいので、パッと見の分かりやすさを優先したためである）。

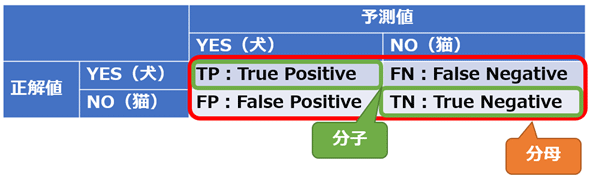
　以上の混同行列の定義を表にまとめたのが図1である。なお、日本語よりも英語の方が直感的に分かりやすいので、英語表記とした。以下の説明ではTP／TN／FP／FNという略語を用いることとする。

図1　混同行列の定義

　この図は非常に有名で、後述の説明のベースともなっているので確実に理解し覚えてほしい。混同行列は、特にこの4種のデータが不均衡（imbalanced data）な場合に役立つ。

　TensorFlow／Kerasで混同行列の値は、

• tf.keras.metrics.TruePositivesクラス（'tp'）
• tf.keras.metrics.TrueNegativesクラス（'tn'）
• tf.keras.metrics.FalsePositivesクラス（'fp'）
• tf.keras.metrics.FalseNegativesクラス（'fn'）

で計算できる。

正解率（Binary Accuracy）

　説明するまでもないが、機械学習モデルによる予測における正解数をデータ数で割った値が正解率である。0.0（＝0％）〜1.0（＝100％）の範囲の値になり、1.0に近づくほどよりよい。

　正解率を混同行列（図2）で説明すると、上記の式の通り、正解率はTP＋TN（陽性予測と陰性予測での正解を足した数）をTP＋FP＋TN＋FN（4種類全部の数）で割った数である。あえて難しく説明している形になっているが、これは後述の適合率や再現率との違いを視認しやすくするためである。

図2　混同行列による正解率の説明

　正解率は、最も典型的で基礎的な評価関数であり、一般人向けにも分かりやすいのでよく用いられる。実際に本連載の第8回でも使用した。二値分類だけでなく、次回解説する多クラス分類でも用いられる。

　ただし正解率の使用には注意が必要である。というのも、確かに正解の二値が均等に分けられている場合は問題がない。しかし正解の二値が不均衡である場合、例えば「猫」が正解のデータが99個あり「犬」が1個しかないという極端な状況の場合、常に「猫」と答えれば99％正解することになる。このような予測を行う学習済みモデルは、正解率は高いものの、価値がないといえる。「犬」を予測したい場合には全く使えないモデルである。この問題に対する（正解率ではなく）適合率や再現率（いずれも後述）は0％を示すので「おかしい」と気付きやすい。

　TensorFlow／Kerasでの正解率の計算には、

• tf.keras.metrics.BinaryAccuracyクラス
• tf.keras.metrics.binary_accuracy()関数

もしくは（compile()メソッドの引数metricsで）、

• 'binary_accuracy'
• 'accuracy'
• 'acc'

という文字列を使えばよい。二値分類で'accuracy'や'acc'を使った場合、自動的にBinaryAccuracyクラスが選択される。

　ちなみに、1.0−正解率は誤答率（Error rate）と呼ばれる。

適合率（Precision）

　機械学習モデルによる予測で陽性（Positive、正例）だった予測全体のうち、正解だった割合が適合率（Precision）である。つまり、機械学習モデルによる予測が陽性だった場合にどれくらい正解に「適合」できるか、ということだ。もちろん100％適合できるのが最良である。

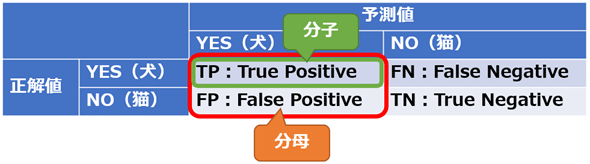
　具体的には上記の式の通り、TP（＝正解＆陽性予測の数）をTP＋FP（＝正解＆陽性予測＋不正解＆陽性予測の数）で割った数値である（図3）。よって、0.0（＝0％）〜1.0（＝100％）の範囲の値になり、1.0に近づくほどよりよい。

図3　混同行列による適合率の説明

　適合率は、精度評価でFP（偽陽性＝不正解＆陽性予測）をできるだけ低くしたい一方で、FN（偽陰性＝不正解＆陰性予測）があまり重要ではなく無視してもよい場合に有用である。

　と言われても分からない人も多いと思うので、例を挙げて説明しておこう。例えばあなたが果物屋さんで「個々のお客さんに対し、りんごの購入が必要かどうか」という二値分類を予測する機械学習モデルを作成したとする。

　このケースでは、「購入が必要」という陽性予測は、より正確で（＝FP：偽陽性ができるだけ低く）なければならないだろう。もし間違ってしまうと、リンゴを買ってもらう機会を損失してしまうからだ。

　一方で、「購入が不要」という陰性予測では、不正解であること（＝FN：偽陰性）はそれほど重要ではない。なぜなら、実際にはリンゴの購入が不要である人に間違ってリンゴの購入をお勧めしてしまったとしても、いずれにしろ買ってはもらえず、結果的にはお店のメリットにはならないからだ。つまり果物屋さんにとっては、売れない予測についてはハズレようと実利面からは無視しても構わず、売れる予測の精度を強化する方がより重要ということである。

　このケースでは、正解率や再現率よりも適合率を採用する方が精度指標として優れていると考えられる。まとめると適合率は、陽性予測においては、できるだけ不正解「FP」は出したくない場合に使えばよい。

　TensorFlow／Kerasでの適合率の計算には、

• tf.keras.metrics.Precisionクラス

を使えばよい。

再現率（Recall）／感度（Sensitivity）

　実際の「真の値（正解値）」が陽性（Positive、例：YES）のデータ全体のうち、機械学習モデルによる予測が正解だった割合が再現率（Recall）もしくは感度（Sensitivity）である。つまり、正解値が陽性である場合において機械学習モデルによる予測がどれくらいその正解を「再現」できるか、ということだ。当然、100％再現できるのが最良である。

　具体的には上記の式の通り、TP（＝正解＆陽性予測の数）をTP＋FN（＝正解＆陽性予測＋不正解＆陰性予測の数）で割った数値である。よって0.0（＝0％）〜1.0（＝100％）の範囲の値になり、1.0に近づくほどよりよい。

　分母の意味が少し分かりづらいが、「陰性予測をして不正解」ということは、つまり「正解値は陽性（Positive、例：YES）」ということである。つまりこの分母TP＋FNは、「実際の正解値が陽性のデータ全体」ということを意味する（図4）。

図4　混同行列による再現率の説明

　再現率は、精度評価でFN（偽陰性＝不正解＆陰性予測、つまり正解は陽性）をできるだけ低くしたい一方で、FP（偽陽性＝不正解＆陽性予測、つまり正解は陰性）があまり重要ではなく無視してもよい場合に有用である。このように再現率は、適合率とは注目しているポイントが異なることに注意してほしい。

　これも何を言っているかが分かりづらいと思うので、例を挙げて説明しておこう。例えばあなたがお医者さんで「健康診断における個々の患者さんに対し、精密検査が必要かどうか」という二値分類を予測する機械学習モデルを作成したとする。

　このケースでは、「精密検査が不要」という陰性予測は、より正確で（＝FN：偽陰性ができるだけ低く）なければならないだろう。もし間違ってしまうと、病気の発見を見逃してしまうことになるからだ。

　一方で、「精密検査が必要」という陽性予測では、不正解であること（＝FP：偽陽性）はそれほど重要ではない。なぜなら、実際には病気ではない人に間違って「精密検査が必要」と診断してしまったとしても、その精密検査では問題が出ずに「健康」と診断されるからだ。つまりお医者さんにとっては、実際に健康な人（正解＝陰性）への予測結果が外れようと安全面からは無視して構わず、実際に病気の人（正解＝陽性）への予測の精度を強化する方がより重要ということである。

　このケースでは、正解率や適合率よりも再現率を採用する方が精度指標として優れていると考えられる。まとめると再現率は、実際の正解値が陽性のデータに対しては、その予測時にできるだけ不正解は出したくない場合（＝陰性予測においては、できるだけ不正解「FN」は出したくない場合）に使えばよい。

　TensorFlow／Kerasでの再現率／感度の計算には、

• tf.keras.metrics.Recallクラス

を使えばよい。

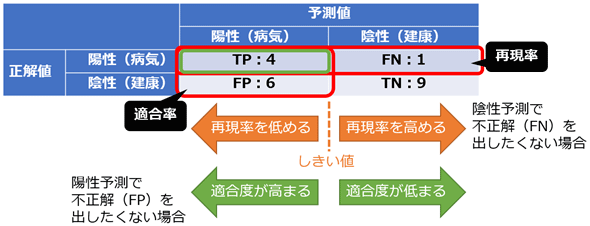
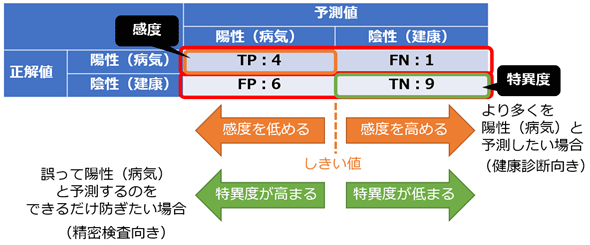
　なお、適合率と再現率には重要な法則がある。通常、両者にはトレードオフの関係がある（図5）。例えば再現率を高くするために、より多くの予測値（範囲は0.0〜1.0とする）が陽性（1.0）になるよう、分類判定のしきい値を中央の0.5から0.3に変更したとする。これにより確かに再現率は高まるが、適合率においては、分母である「陽性予測全体の数」が増えることになる。それと同等に分子であるである「陽性予測＆正解の数」が増えない限り、つまり通常は適合率が小さくなるのである。逆に再現率を低くすると、適合率は高まる可能性が高い。このトレードオフ関係を利用して、再現率のしきい値（例えば0.3以上など）を指定してベストな適合率を計算するためのPrecisionAtRecallクラスが、TensorFlow／Kerasには用意されている。

図5　適合率と再現率のトレードオフ

特異度（Specificity）

　先ほどの感度（＝再現率と同じもの）は、正解値が「陽性」である場合の正解率を測る精度指標だった。その別パターンで、正解値が「陰性」である場合の正解率を測る精度指標もある。それが特異度（Specificity）である。特異度は、感度（Sensitivity）に対立する概念として使われるので、これについても説明しておこう。両者の違いを例で説明すると、以下のようになる。

• 感度： 例えば「何らかの病気であると正しく判別される割合」など
• 特異度： 例えば「何の病気でもないと正しく判別される割合」など

　例えば健康診断であれば、検査の感度（誤検出も含めた検出率）が高いほど好ましい。感度が高い状況では、病気である可能性のある人をできるだけ広く検出する。「少しでも問題がありそうであれば、精密検査を受けてもらう」という方が病気を見落とさない確率が高まるというメリットがある。

　一方、例えばその精密検査であれば、今度は特異度が高いほど好ましい。特異度が高い状況では、病気ではない人が「病気だ」と判定されることはめったにない、つまり「特異」なことである。もし、健康な人を誤って病気だと判定してしまう方が、医者としてリスクが大きいと思われるのでこの方がよいのである。

　感度と特異度は基本的にトレードオフの関係にあり、通常、感度を高めると特異度が低くなり、特異度を高めると今度は感度が低くなる（図6）。

図6　感度と特異度のトレードオフ

　実例と意味から説明したが、先ほどと同様に定義と数式も紹介しておこう。

　実際の「真の値（正解値）」が陰性（Negative、例：NO）のデータ全体のうち、機械学習モデルによる予測が正解だった割合が特異度（Specificity）である。

　具体的には上記の式の通り、TN（＝正解＆陰性予測の数）をFP＋TN（＝不正解＆陽性予測＋正解＆陰性予測の数）で割った数値である。よって0.0（＝0％）〜1.0（＝100％）の範囲の値になり、1.0に近づくほどよりよい。

　これも分母の意味が少し分かりづらいが、「陽性予測をして不正解」ということは、つまり「正解値は陰性（Negative、例：NO）」ということである。つまりこの分母FP＋TNは、「実際の正解値が陰性のデータ全体」ということになる（図7）。

図7　混同行列による特異度の説明

　TensorFlow／Kerasでの特異度の計算には、単純に特異度を計測するSpecificityクラスは用意されていない。しかし、感度のしきい値を指定したうえで、その指定値以上の結果から特異度が最大である値を返す、

• tf.keras.metrics.SpecificityAtSensitivityクラス

が用意されている。逆に、特異度のしきい値を指定したうえで、その指定値以上の結果から感度が最大である値を返す、

• tf.keras.metrics.SensitivityAtSpecificityクラス

も用意されている。

F値（F-measure、F-score）／F1スコア（F1-score）

　「感度と特異度のトレードオフ」の話を挟んだが、再度、1つ前の「適合率と再現率のトレードオフ」（前掲の図5を参照）に話を戻す。適合率と再現率のトレードオフ関係に着目し、調和平均（詳細後述）を算出した値がF値（F-measure）もしくはFスコア（F-score）である。

　なお調和平均（Harmonic Mean）とは、平均を計算する手法の一つで、“率”の平均を算出するのに適している（※ちなみに通常の算術平均は、“量”の平均を算出するのに適している）。F値の場合は、適合“率”と再現“率”の平均を算出しているというわけだ。例えばpとrという2つの“率”の調和平均を算出する式は以下のようになる。

　この数式は、例えば小学校では2つの時速という“率”の平均を算出するのに使われている。例題を挙げると、p＝時速4kmとr＝時速6kmの調和平均値は、2×（4×6）／（4＋6）＝2×（24）／（10）＝4.8となり、時速4.8kmが答えである。

　調和平均の計算式におけるpをPrecision（適合率）、rをRecall（再現率）と置くと、下記の計算式になる（※途中の計算式は煩雑なので一部省略した。気になる人は紙に書いて計算してみてほしい）。

　具体的には上記の式の通り、2×適合率×再現率を適合率＋再現率で割った数値である。この調和平均の計算値は、F₁スコア（F₁ score）と呼ばれる。F値は0.0（＝0％）〜1.0（＝100％）の範囲の値になり、1.0に近づくほどよりよい。1.0に近い、つまり適合率と再現率の両方が同時にできるだけ高いのが、「最も効率よくバランスのとれた機械学習モデル」と言えるのである。

　と言われても、なかなかイメージが湧かない人も多いと思うので、例を挙げて説明しておこう。あなたがお医者さんで「受診者の病気を発見したい」とする。そこで「病気かどうか」という二値分類を予測する機械学習モデルを作成したとする。

　例えば健康診断では病気である人を見逃したくないため、再現率が重要である（＝前述の解説を再掲すると、「陰性予測においては、できるだけ不正解『FN』は出したくない」ということだ）。

　例えば精密検査では病気でない人を誤診したくないため、適合率が重要である（＝前述の解説を再掲すると、「陽性予測においては、できるだけ不正解『FP』は出したくない」ということだ）。

　今回は健康診断でも精密検査でもなく、これらの両者のバランスが最もよくなるように（＝調和平均値が1.0に近くなるように）診断したいという場合に、評価関数としてF₁スコアを用いればよいというわけだ。

　TensorFlow／Kerasでは、F値を計算するクラスや機能は提供されていないため、適合率と再現率から算出するコードを独自に実装する必要がある。その実装方法については、次の項目でまとめて紹介する。

　さて、ここまでF₁スコアという最もベーシックなF値を説明してきたが、より柔軟なF値を計算するためのバージョンもある。そこで次に、それについて説明する。

重み付きF値（Weighted F-measure）／Fβスコア（Fβ-score）

　上記のF値／F₁スコアの解説では、調和平均という計算方法を活用した。これは適合率と再現率をどちらも同じように扱いたい場合に有用ではあるが、どちらかをより重視したいというニーズもあるだろう。そこで、先ほどの調和平均の計算式のr（つまり再現率）の方に「重み（weight）」を意味するβ²を掛けてみることにしよう（※なお、pつまり適合率の方には暗黙的に1²の重みを掛けているものと見なしてほしい）。この内容で、重み付き調和平均（Weighted Harmonic Mean）を算出する式は以下のようになる。

　F値と同様の例題を挙げておこう。重みの意味は後述するが、ここでは2.0を指定してみる（＝rを2倍重視するといったイメージになる）。この場合、p＝時速4kmとr＝時速6kmでの重み付き調和平均値は、（1＋2²）×（4×6）／（2²×4＋6）＝（5）×（24）／（22）＝約5.45となり、時速5.45kmが答えである。

　重み付き調和平均の計算式におけるpをPrecision（適合率）、rをRecall（再現率）と置くと、下記の計算式になる（※途中の計算式は煩雑なので一部省略した。気になる人は紙に書いて計算してみてほしい）。

　具体的には上記の式の通り、(1＋重み²) × 適合率 × 再現率を重み² × 適合率＋再現率で割った数値である。この重み付き調和平均の計算値は、重み付きF値（Weighted F-measure）もしくはF_βスコア（F_β score）と呼ばれる。重み付きF値は先ほどと同様に、0.0（＝0％）〜1.0（＝100％）の範囲の値になり、1.0に近づくほどよりよい。

• β＝0.0： 適合率しか見ない
• 0.0＜β＜1.0： 適合率を指定した比率でより重視する
• β＝1.0： 適合率と再現率を同等に扱う（＝F₁スコアと同じ結果）
• 1.0＜β＜∞： 再現率を指定した倍数でより重視する

　β値を実際にどのような値にするかは試行錯誤が必要になるが、イメージしやすい目安として、例えば再現率が2倍ほど重要な場合には、まずはβに2.0などを指定してみるとよいだろう（F₂ score）。また目安として、適合率を50％ほど（再現率よりも）重視したい場合には、まずはβに0.5（＝1.0−0.5）などを指定してみるとよいだろう（F_0.5 score）。

　前述の通り、TensorFlow／Kerasでは、F値を計算するクラスや機能は提供されていない（※こちらの記事「KerasでF1マクロを計算する方法は？ - スタックオーバーフロー」によると、理由があって機能が削られたようである）。適合率や再現率を取得する機能はあるので、それらを使って計算式を組み立てれば、F₁スコアやF_βスコアは計算できるはずだ。リスト1は筆者によるその実装例である（といっても、先ほどの数式をそのままPythonコードで表現しただけである）。

###########################################
# 関数定義（下記の2行のみ）

# ※F1スコアはbetaの指定は不要。Fβスコアのときだけbetaを指定する
def f_measure(precision, recall, beta=1.0):
  return (1 + beta**2) * (precision * recall) / (beta**2 * precision + recall)

###########################################
# 上記関数の使用例
import numpy as np
import tensorflow as tf

# サンプルデータの作成
y_true = np.array([0, 1, 1, 0, 1, 1, 1, 0, 0, 0])
y_pred = np.array([0, 1, 0, 0, 0, 1, 1, 1, 0, 0])
# TP＝3、TN＝4、FP＝1、FN＝2、合計＝10

# 適合率
p_metric = tf.keras.metrics.Precision()
p_metric.update_state(y_true, y_pred)
precision = p_metric.result().numpy()
print(precision) # 0.75＝TP／（TP＋FP）＝3／（3＋1）

# 再現率
r_metric = tf.keras.metrics.Recall()
r_metric.update_state(y_true, y_pred)
recall = r_metric.result().numpy()
print(recall) # 0.6＝TP／（TP＋FN）＝3／（3＋2）

# 重み（Fβスコアの場合）。F1スコアの場合は1.0にするか指定しない
beta = 2.0

# F値（Fβスコア）の計算結果（上記関数の呼び出し）
score = f_measure(precision, recall, beta)
score # 0.625
      # ＝（1＋beta**2）×（Precision×Recall）／（beta**2×Precision＋Recall）
      # ＝（1＋4）×（0.75×0.6）／（4×0.75＋0.6）
      # ＝（5）×（0.45）／（3.6）

リスト1　F1／Fβを計算するためのカスタム関数の実装例

---

　以上、今回は二値分類用［基礎編］の評価関数を説明した。次回は、今回を踏まえて、二値分類用［応用編］や多クラス分類用の評価関数について解説する。

「TensorFlow 2＋Keras（tf.keras）入門」