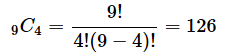［数学×Python］再帰呼び出しをマスターしよう：数学×Pythonプログラミング入門（4/4 ページ）

» 2022年03月17日 05時00分公開

練習問題

　それでは、練習問題に取り組み、ここまで見てきた再帰のプログラミングを確実に身に付けましょう。練習問題についても、考え方を中心に動画で説明しています。再帰は考え方さえ理解できれば簡単です。コードを見ても訳が分からないという方はぜひ動画を視聴して、考え方を押さえておいてください。

動画4　再帰呼び出し（数学の漸化式）の練習問題

（1）経路の数を求める

　最初の問題はまた魔王と勇者に登場してもらいます。なんとか魔王を倒した勇者ですが、それでもまだ世界に平和は訪れません。まだ、ダンジョン（迷宮）の中にラスボスがいるようです。図5のようなダンジョンがあるとき、後戻り（上に移動したり、左に移動したり）はしないものとして、ラスボスにたどり着くまでの道は何通りあるでしょうか。再帰を使って、その数を求める関数を作成してみてください（図中の数字や記号は後のヒントで説明します）。

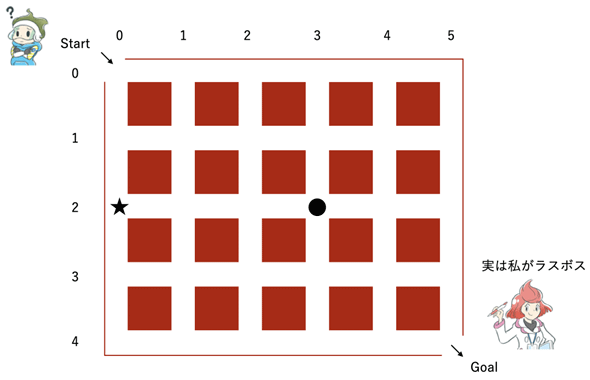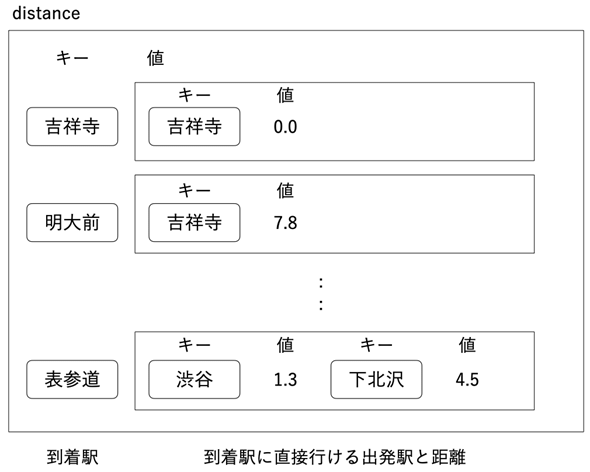
図5　スタートからゴールまで何通りの行き方があるか
数字は通路の番号。この場合、5行6列となる。交差点は行番号と列番号で表されるので、★の位置は[2][0]に当たり、●の位置は[2][3]に当たることが分かる。

　関数名はcountroute_mとしましょう。ダンジョンの行と列の数がいくらであってもいいように、countroute_m(行数, 列数)で呼び出せるようにしてください。計算量が増えないようにするためにメモ化は必須です。

（ヒント）
　★の位置には上からしか来られないので、そこに行く方法は1通りです。一方、●に行くには上から来るか、左から来るかです。答えは126通りです。5行6列の場合、インデックスは行が4まで、列が5までであることに注意してください。

（2）最短経路の距離を求める（やや難）

　出発点から目的地へ行くためには、普通は幾つもの経路が考えられます。例えば、鉄道を使って東京の吉祥寺から表参道まで行くには、図6のような経路があります。数字は距離（km）です。

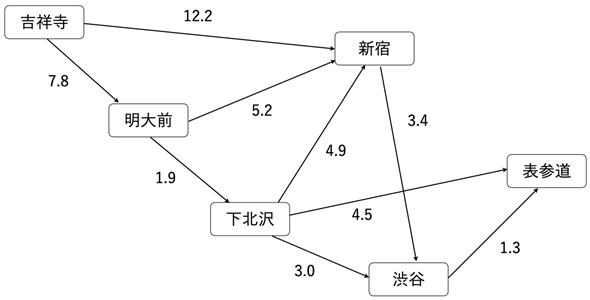図6　吉祥寺から表参道までの経路の例
経路はこれ以外にもあるが簡単なものにした。列車種別による時間の違いや乗り換え時間、乗り換え回数、運賃なども含めて考えれば、路線案内のプログラムが作成できるが、ここでは、距離のみに注目する。

　吉祥寺から表参道までの最短距離を再帰的に求める関数searchを作成し、実行してみてください。経路を求める必要はありません（最短距離だけで構いません）。

　経路のデータはリスト11の辞書型データdistanceとして定義されているものとし、終点と経路のデータを指定すれば最短距離が求められるようにします。辞書型データの中に辞書型データがあるのでやや複雑ですが、辞書型データの扱いに慣れていない方は後の（ヒント2）の図解とコード例を参考にしてください。

distance = {'吉祥寺' : {'吉祥寺': 0},
            '明大前' : {'吉祥寺': 7.8},
            '下北沢' : {'明大前': 1.9},
            '新宿' : {'吉祥寺': 12.2, '明大前': 5.2, '下北沢': 4.9},
            '渋谷' : {'新宿': 3.4, '下北沢': 3.0},
            '表参道' : {'渋谷': 1.3, '下北沢': 4.5}}

search('表参道', distance) # 実行例
# 出力例：14.0

リスト11　吉祥寺から表参道までの最短距離を求める
経路のデータdistanceは、到着駅をキーとする辞書になっている。辞書distanceの中の個々の要素は、到着駅から直接行ける出発駅をキーとし、そこからの距離を記録した辞書となっている。例えば、distanceの最後の行は「表参道へは、渋谷から1.3km、下北沢から4.5km」という意味になる*5。関数searchに到着駅と経路のデータを指定すると、吉祥寺からの最短距離が求められるようにする。

*5　最短経路を求める問題では、これとは逆に、出発駅をキーとし、それに対する値として「出発駅から直接行ける到着駅と距離」を記録する方法が一般的です。しかし、ここでは、これまでに説明した再帰のアルゴリズムができるだけ素直に適用できるようなデータ構造としました（到着駅からたどっていくか、出発駅からたどっていくかだけの違いです）。

　これは「緩和」を利用する問題です。考え方は目標3で見たものと全く同じなのですが、辞書を使ってデータを記録してあることと、直前の値の数が一定ではないというところがちょっと扱いにくいかもしれません。そこで、リスト12のコードの穴埋めで答えていただくことにしましょう。なお、このままだと計算量が大きくなってしまいますが、メモ化は行わなくて構いません。メモ化を行った例は解答例のところで紹介します。

def search(goal, data): # 到着駅から直接行ける場所までの最短距離を得る
if goal == ア: # 始点なら0.0を返す
    return 0.0
else:
    prevdata = data.get(goal) # 到着駅と出発駅の距離の一覧(辞書型)
    # 複数の候補の中から、最短距離を求める
    w = [] # 最短距離の候補を記録する作業用のリスト
    for start in prevdata.keys(): # 直前の出発駅全てについて
      # 直前の出発駅までの最短距離を再帰的に求める(出発駅を到着駅として呼び出す)
      w.append(イ + prevdata.get(start)) # 最短距離の候補を記録
    return min(w) # 候補の中の最短のものを返す

リスト12　吉祥寺から到着駅までの最短距離を求める関数search
関数searchでは、リストwに最短距離の候補を記録しておき、その中の最小値を返す。直前の出発駅がいくつあるかは決まっていないので、for文を使って全ての出発駅について、直前の出発駅までの最短距離（イ）と、到着駅から直前の出発駅までの距離（prevdata.get(start)）を求め、その和を作業用のリストwに追加していく。最後にwの最小値を返す。例えば、goalが'表参道'なら、wには「渋谷までの最短距離＋渋谷から表参道の距離」と「下北沢までの最短距離＋下北沢から表参道の距離」を記録し、最小値を求める。渋谷までの最短距離や下北沢の最短距離は（イ）で再帰的に求める。

（ヒント1）考え方は以下の通りです。

到着駅が吉祥寺であれば0.0を返す
到着駅に直接行ける出発駅を求める（個数は決まっていない）
「出発駅までの最短距離」+「出発駅から到着駅までの距離」の最小値を求める

　直前の出発駅までの最短距離がすでに求められているものとすれば、それに到着駅までの距離を加えたものの最小値が、到着駅までの最短距離になります。例えば、

表参道までの最短距離は「渋谷までの最短距離」+「渋谷から表参道までの距離」と「下北沢までの最短距離」+「下北沢から表参道までの距離」の小さい方
さらに、渋谷までの最短距離は「新宿までの最短距離」+「新宿から渋谷までの距離」と「下北沢までの最短距離」+「下北沢から渋谷までの距離」の小さい方

　「出発駅までの最短距離」は再帰的に求めていけますね。

（ヒント2）
　リスト11の辞書型データdistanceの構造は図7の通りです。

図7　経路を表す辞書型データの構造

　辞書distanceでは、キーは「到着駅」、それに対する値は「到着駅に直接行ける出発駅と距離」の辞書型データとなっている。

　例えば、以下のように、distanceのgetメソッドにキーとして'表参道'を指定すると、表参道に直接行ける出発駅と距離の辞書型データが取得できます。

prevdata = distance.get('表参道')
print(prevdata)
# 出力例：{'渋谷': 1.3, '下北沢': 4.5}

　prevdataも辞書型になっているので、以下のようにすれば、渋谷からの距離である1.3が得られます

prevdata.get('渋谷')
# 出力例：1.3

　さらに、表参道から直接行ける出発駅の全ての距離を求めるには、keysメソッドで取得したキーの一覧を使い、値を取得します。

prevdata = distance.get("表参道") # 出発駅と距離
for start in prevdata.keys(): # prevdataの全てのキーについて
print(prevdata.get(start))

# 出力例：
# 1.3 # 渋谷から表参道までの距離
# 4.5 # 下北沢から表参道までの距離

練習問題の解答例

　以下、解答とプログラムの作成例です。もちろん、異なるやり方もあるので、これらが唯一の答えというわけではありません。

（1）経路の数を求める

　ヒントから分かるように、0行目や0列目を進む方法は1通りです。従って、0行目と0列目には全て1を入れておきます（二次元のリスト全体に1を入れておけばよい）。それ以外は上から来るか、左から来るかなので「上から来る場合の数＋下から来る場合の数」で求められます。漸化式を数式として表さなくても、リスト13のようなコードが書けますね。実は、このコードはパスカルの三角形を求めるコードと全く同じです。

def countroute_m(n, m): # 行数と列数を指定
def countroute(row, col): # インデックスを指定
    if row==0 or col==0: # 0行目や0列目を進む方法は1通り
      return 1
    elif memo[row][col] != 1: # 上記以外でメモが記録されている
      return memo[row][col]
    else: # 上から来るか、左から来るか
      memo[row][col] = countroute(row, col-1) + countroute(row-1, col)
      return memo[row][col]

memo = [[1 for _ in range(m)] for _ in range(n)] # 記録前は全て1
return countroute(n-1, m-1) # インデックスの最大値を指定して呼び出す

countroute_m(5, 6)
# 出力例：126

リスト13　n行m列の経路を通る方法が何通りあるかを求める
関数countroute_mには行数と列数を指定するが、関数countrouteでは行と列のインデックスを指定する必要があることに注意。n行m列の通路があれば、ゴールは[n-1][m-1]の位置になる。

　高校数学では、縦の4つの通路と横の5つの通路（全部で9個）を必ず通るので、それらを並べ替える組み合わせ数を以下のようにして求めれば答えが得られます。

　個人的な話をすると、私はこういう順列・組合せの問題がものすごく苦手でした。が、プログラミングで再帰を学んでからは「なんだ、コンピュータにやらせれば悩まなくて済むじゃん」と気がラクになっただけでなく、問題がずいぶんとクリアに見えるようになった気がします。

（2）最短経路の距離を求める

　到着駅から吉祥寺までを逆にたどっていけばいいので、アは'吉祥寺'となります。イでは、直前の出発駅にたどり着くための最短距離を求めたいので、関数searchの引数goalにstartを指定して再帰的に呼び出せばいいですね。それまで出発駅だったものを、到着駅に指定してそこまでの最短距離を求めるというわけです。

（答え）オレンジ色の部分をクリックすると答えが表示されます。

ア. 　'吉祥寺'　
イ. 　search(start, data)

　念のため、コード全体を全て示しておきます（リスト14）。

def search(goal, data): # 到着駅から直接行ける場所までの最短距離を得る
if goal == '吉祥寺': # 始点なら0.0を返す
    return 0.0
else:
    prevdata = data.get(goal) # 直前の出発駅からの距離の一覧(辞書型)
    # 複数の候補の中から、最短距離を求める
    w = [] # 最短距離の候補を記録する作業用のリスト
    for start in prevdata.keys(): # 直前の出発駅全てについて
      # 直前の出発駅までの最短距離を再帰的に求める（出発駅を到着駅として呼び出す）
      w.append(search(start, data) + prevdata.get(start)) # 最短距離の候補を記録
    return min(w) # 候補の中の最短のものを返す

リスト14　吉祥寺から到着駅までの最短距離を求める関数search（完成形）
目標3の「ダメージのある階段」の例では、2つのうちのどちらか小さい方を選んだが、この問題では「緩和」の計算をするための最小値の候補の個数が決まっていないので、いくつかの候補の中の最小値を選ぶ。

　リスト14をメモ化した例も紹介しておきましょう。リスト15の例では、メモも辞書型のデータとします。関数の定義から実行までのコード全体を掲載しておきます。

def search_m(goal, data):
def search(goal, data): # goalから直接行ける場所までの最短距離を得る
    if goal == '吉祥寺': # 始点なら0を返す
      return 0.0
    else:
      prevdata = data.get(goal) # goalの直前の駅と距離の一覧（辞書型）
      w = [] # 最短距離の候補を記録する作業用のリスト
      for start in prevdata.keys(): # 直前の駅全てについて
        # 直前の駅までの最短距離を再帰的に求める
        if memo.get(start) is not None: # メモから得る
          m = memo.get(start)
        else:
          m = search(start, data)
          memo[start] = m
        w.append(m + prevdata.get(start)) # 最短距離の候補を記録
      return min(w) # 候補の中の最短のものを返す

memo = {}
return search(goal, data)

# 実行する
distance = {'吉祥寺' : {'吉祥寺': 0.0},
            '明大前' : {'吉祥寺': 7.8},
            '下北沢' : {'明大前': 1.9},
            '新宿' : {'吉祥寺': 12.2, '明大前': 5.2, '下北沢': 4.9},
            '渋谷' : {'新宿': 3.4, '下北沢': 3.0},
            '表参道' : {'渋谷': 1.3, '下北沢': 4.5}}

search_m('表参道', distance)

リスト15　関数searchをメモ化した例
memoは、最初は空の辞書{}にしておく。getメソッドを使って、memo.get(キー)と書けば、キーが存在しない場合には既定値（指定されていない場合はNone）が返されるので*6、それによりメモにその駅までの最短距離の記録が存在しているかどうかを調べている。辞書memoにデータを追加するには、memo[キー] = 値と書けばよい。

*6　memo[キー]だけでも、キーに対する値が得られますが、その書き方では、キーが存在しないとエラーになります。

　最後に補足ですが、メモから値を得るコードはちょっと冗長な感じがしますね。以下に抜き出してみますが、getメソッドを2回呼び出しています。

if memo.get(start) is not None: # メモから得る
m = memo.get(start)

　Python 3.8からは、:=演算子（セイウチの顔を横にした形に似ているのでセイウチ演算子とも呼ばれます）を使って、以下のように書くことができます。

if tmp := memo.get(start) is not None: # メモから得る
m = tmp

　このように書けば、getメソッドの呼び出しは1回だけで済みます。ただし、現時点（2022年2月28日時点）ではGoogle Colabの標準的な環境がPython 3.7なので、残念ながら:=演算子は使えません。

　プログラミングによる問題解決には、漸化式が大いに役立ちます。今回は、漸化式の立て方を通して、再帰のプログラミングに取り組みました。また、再帰の基本的な理解だけでなく、動的計画法にも少し踏み込んでみました。この先には、実用に役立つさまざまなアルゴリズムがあります。今回の内容を十分身に付ければ、そういった問題にも取り組みやすくなると思います。

　さて、次回はまた「計算」に重点を置き、機械学習・ニューラルネットワークなどの基礎となる線形代数（ベクトルや行列）について見ていくこととします。