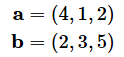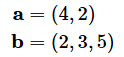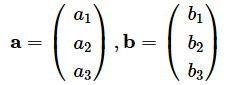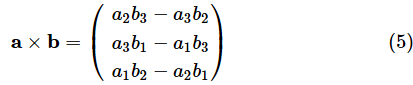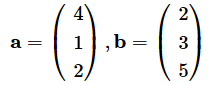Pythonで線形代数！ 〜ベクトル編〜：数学×Pythonプログラミング入門（4/5 ページ）

[羽山博，著]

目標4： ベクトルの外積と直積

　ベクトルの外積については、高校の数学では大きく扱われていないので、なじみのない方も多いかもしれません。しかし、NumPyで提供されているcross関数を使えば、理屈を知らなくてもベクトルの外積を求めることができます。そこで、

のときに、これらのベクトルの外積を求めてみてください。もちろん、外積がどのようなもので、どのような計算で求められるのかを知らないと意味がありませんが、まずは計算できることを優先し、定義や計算方法については後で見ることにします。なお、cross関数で求められる外積はクロス積とも呼ばれます。

　また、NumPyには、直積（ちょくせき）を求めるためのouterと呼ばれる関数も用意されています。実は、outer関数で求められる直積のことを外積と呼ぶ場合もあるので、紛らわしいのですが、ここではcross関数で求められるものを外積、outer関数で求められるものを直積と呼びます。outer関数で求められる直積は全ての要素を掛け合わせた組み合わせになります。こちらについても理屈抜きで、

の直積を求め、どのような結果が得られるか確認してみてください。行列については今回のテーマではないので、詳しくは触れませんが、ベクトル同士の直積は行列になります。

4 ベクトルの外積と直積を求める

　外積を求める例から見ていきましょう。コードと実行例はリスト14の通りです。cross関数を呼び出すだけなので簡単ですね。

import numpy as np

a = np.array([4, 1, 2])
b = np.array([2, 3, 5])

print(np.cross(a, b))
# 出力例：
# [ -1 -16  10]

リスト14　ベクトルの外積を求める
ベクトルの内積はスカラーだが、ベクトルの外積はベクトルになる。外積の定義や計算方法については、後で説明する。

　結果を見ただけでは、外積がどのような計算によって求められたのかちょっと分かりませんね。そこで、外積の定義から見ていきます。3次元空間におけるベクトルの外積は以下のように定義されます。

としたとき、aとbの外積a×bは、

となります*4。

*4　ここでは、ベクトルの要素を見やすくするために、要素を縦に並べて書きました。このような表し方のベクトルを列ベクトルと呼びます。一方、a＝(a₁,b₂,b₃)のように、要素を横に並べた場合は行ベクトルと呼びます。

　（5）式の計算は複雑に見えますが、単なる四則演算です。リスト11の例で確認してみます。一つ一つ丁寧に計算していきましょう。確認のために穴埋めにしておきます。オレンジ色の部分をクリックまたはタップすると答えが表示されます。

なので、これらの値を（5）式に当てはめると、

（答え： ［ア］＝　5　、［イ］＝　2　、［ウ］＝　2　、［エ］＝　4　、［オ］＝　4　、［カ］＝　2　）

となり、リスト14の実行結果と合っていることが分かります。次回お話する行列式を使うともう少しスッキリと表せるのですが、取りあえず、地道に計算して少し慣れておきましょう。

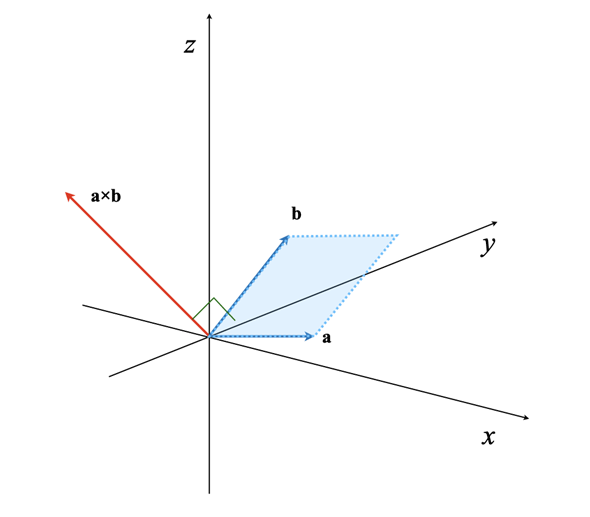
　ところで、計算方法は分かったものの、外積が何を意味するかはちょっと謎ですね。図4を見ていただくと、図形的な意味が分かるかと思います。

図4　外積の図形的な意味
a×bは、aとbに対して垂直なベクトルになる。また、a×bの長さはaとbで作られる平行四辺形の面積に等しくなる。

　aとbの外積a×bは、aとbに対して垂直なベクトルです。つまり、aとbで作られる平面に対して垂直となります。また、a×bの長さはaとbで作られる平行四辺形の面積に等しくなります。従って、|a×b|＝|a| |b| sinθで求められます（θはaとbのなす角度です）。

　a×bの向きは、aからbに向かってネジ（右ネジ）を回したときに、ネジが進む方向と一致します。b×aの場合は、a×bと逆の方向になります。ということで、

であることも分かります。

　次に、直積を求めるouter関数の利用例を見ておきます。

import numpy as np

a = np.array([4, 2])
b = np.array([2, 3, 5])

print(np.outer(a, b))
# 出力例：
# [[ 8 12 20]
#  [ 4 6 10]]

リスト15　ベクトルの直積を求める
ベクトルの直積は行列になる。この例であれば、aの4をbの[2, 3, 5]に掛けたものが1行目になり、aの2をbの[2, 3, 5]に掛けたもののが2行目になっていることが分かる。

　直積の計算方法を図で表すと図5のようになります。見やすくするために、a, bを列ベクトルとして表します。

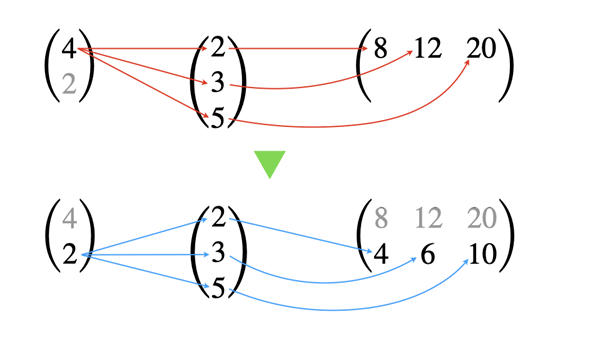図5　直積の計算方法
直積は全ての要素を全ての要素に掛けて求める。結果は行列になる。aの1つ目の要素をbの各要素に掛けたものが行列の1行目になり、aの2つ目の要素をbの各要素に掛けたものが行列の2行目になる。ベクトルの要素数が異なっても同様に計算していけばよい。

　一般に、m次元ベクトルとn次元ベクトルの直積は、m行n列の行列になります。また、m行n列の行列とp行q列の行列の直積は、mp行nq列の行列になります。リスト12では、2次元ベクトルと3次元ベクトルの直積を求めているので、結果は2行3列の行列になっています。

　以上、ベクトルの取り扱いについての基本をざっと見てきました。次回のテーマである行列に取り組む上での前提ともなっているので、特に、和／差／要素ごとの積、内積の計算方法と利用する関数について、きちんと理解しておきましょう。