Pythonで線形代数！ 〜ベクトル編〜：数学×Pythonプログラミング入門（1/5 ページ）

AI／機械学習で使われるデータを表現するためにはベクトルや行列などの線形代数を理解することが必要不可欠。今回はベクトルを中心に、その考え方や各種計算のプログラミング方法を初歩から見ていく。

[羽山博，著]

連載目次

　前回は、漸化式の立て方と再帰呼び出しのプログラミングに取り組み、「現実の問題をどのようにして定式化するか」といった「考え方」についても学びました。

　今回と次回は線形代数のプログラミングを見ていきます。前回と打って変わって、どちらかというと「計算をいかに効率よくこなすか」というお話が中心になります。そのために、NumPyの機能や関数を利用し、さまざまな計算を行う方法を紹介します。

　この連載では既にNumPyの高度な機能も利用していますが、あらためて初歩から確実に身に付けていくことを目標とします。今回は主にベクトルを取り上げ、行列の取り扱いについては次回のテーマとします。

　今回の練習問題としては、ある点から直線や平面までの距離を求めるプログラムと、視神経のニューロンの働きをシミュレートするプログラムに取り組みます。

　なお、高校の数学ではベクトルを

のように矢印を付けて表しますが、ここでは

のように太字で表すことにします。

連載：

『数学×Pythonプログラミング入門 ― 中学・高校数学で学ぶ』

この連載では、中学や高校で学んだ数学を題材にして、Pythonによるプログラミングを学びます。といっても、数学の教科書に載っている定理や公式だけに限らず、興味深い数式の例やAI／機械学習の基本となる例を取り上げながら、数学的な考え方を背景としてプログラミングを学ぶお話にしていこうと思います。

羽山博

筆者紹介： IT系ライター、大学教員（非常勤）。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く99回で一旦中断。さらにリターンライダーを目指し、大型二輪免許を取得するもバイクの購入資金が全くない。

目標1： ベクトルの和・差・スカラー倍

　ウォーミングアップをかねて、ベクトルの基本的な計算から始めましょう。a＝(2,3)とb＝(4,1)があるとき、以下の計算を行うコードを書いてみてください。

• a＋b　…… ベクトルの和　
• a−b　…… ベクトルの差
• a×2　…… ベクトルのスカラー（定数）倍

　また、各要素のべき乗を求めてみてください。例えば、a＝(2,3)の各要素を2乗した(4,9)を求めるコードを書いてみてください*1。

*1　数学では、a＝(2,3)の2や3に当たるそれぞれの値のことを「成分」と呼びますが、ここでは「要素」と呼ぶことにします。

　ベクトルは、PythonのリストやNumPyの配列（ndarray）を使って表せますが、決まり切った計算を行うには繰り返し処理を使ってリストの要素を1つずつ計算するより、NumPyの便利な関数やブロードキャスト機能を使った方が断然簡単です。基本の基本なのでサクッと行きましょう。

　ただし、ベクトルについてあやふやなところがある方は、ここで簡単におさらいしておきましょう。ベクトルとは、大きさと方向を持った量で、図1の矢印のようなイメージで捉えることができます。また、ベクトルは基準の位置を決めたときのある点の位置を表すためにも使われます。そのような使い方のベクトルを位置ベクトルと呼びます。基準の位置が原点(0,0)である場合は、位置ベクトルを「座標を表すもの」と考えてもらっても問題はありません。さらには、ものごとの性質などを表すために、単に数値や式をいくつか並べたものと考えても構いません。

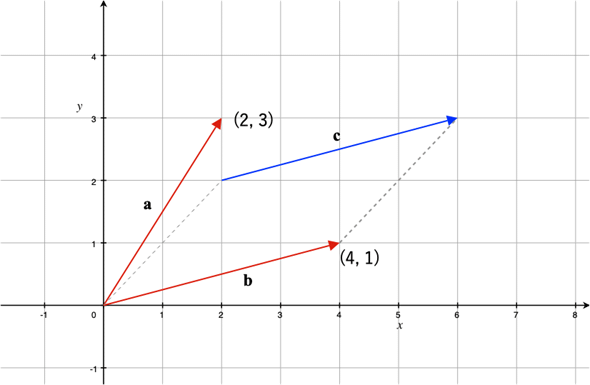図1　ベクトルとは
ベクトルとは、a,b,cのように向きと長さを持った量のこと。bとcは向きと長さが等しいベクトルなので、b＝cと見なせる。また、aやbのように、基準点を決めたときの(2,3)や(4,1)などの位置を表すベクトルを位置ベクトルと呼ぶ。ここでは、基準点は原点(0, 0)となっている。

　ベクトルに対して、a×2の「2」のような単一の値はスカラーまたは定数と呼ばれます。

1. ベクトルの和／差／スカラー倍のコードを書く

　ベクトルをNumPyの配列（ndarray）として表すには、numpyモジュールのarray関数を使います。まず、a＝(2,3)とb＝(4,1)を作成しましょう（リスト1）。以下、コードの説明で特に明示する必要のない場合には、

• Numpyの配列のことを単に配列と呼び
• Numpyの配列を使って表されたベクトルのことを単にベクトルと呼ぶ

ことにします。

import numpy as np

a = np.array([2, 3])
b = np.array([4, 1])

print(a)
print(b)
# 出力例：
# [2 3]
# [4 1]

リスト1　ベクトルをNumPyのndarrayとして表す
numpyモジュールのarray関数に1次元のリストを指定すると、ベクトルが作成できる。作成したベクトルの値をprint関数を使って表示すると［］の中に各要素をスペースで区切って並べた形式で出力（表示）される。一方、print(b)の代わりに、単にbと書いて式の値をそのまま返すとarray([4, 1])と表示される。

　array関数では、引数のリストの要素が全て整数であれば、通常、64ビット整数のベクトルが作成されます。ただし、小数点付きの要素が含まれていれば、64ビット浮動小数点数の配列となります。明示的にデータ型を指定したいときには、array関数のdtype引数にデータ型を指定します。これ以降のコードでは、特に明記していない場合、import numpy as npが書かれているものとして話を進めます。

（例）

• np.array([255, 256, 257], dtype=np.uint8) …… 8ビット符号なし整数のベクトル(255, 0, 1)
• np.array([255, 256, 257], dtype=np.float32) …… 32ビット浮動小数点数のベクトル(255.0, 256.0, 257.0)

　8ビット符号なし整数の場合、256は二進数で9桁の100000000と表されるので、先頭の1が落ちてしまいます。上の例で、256が0に、257が1になるのはそのためです。8ビット符号なし整数は、値の範囲が0〜255なので、グレースケール（0が黒で255が白）や、RGB値（赤／青／緑の値をそれぞれ0〜255で表す）のカラーコードを表す場合によく使われます。

　なお、全ての要素が0のベクトルは零（ゼロ）ベクトルと呼ばれ、太字の0で表されます。np.zeros(n)とすると、要素数（次元数)がn個の零ベクトルが作成できます。ただし、zeros関数では、データ型を指定しないと浮動小数点数とみなされるので、全ての要素が0.0となります。また、np.ones(n)なら、全ての要素が1.0で、要素数（次元数)がn個のベクトルが作成できます。

　話が少し脇にそれてしまいました。ベクトルが作成できたので、和／差／スカラー倍を求めましょう。ベクトルの和は+演算子で、差は-演算子で求められます。スカラー倍するには*演算子を使います（リスト2）。

　これ以降は数値の計算だけで答えが求められるので図解は含めませんが、念のため、高校の数学で学んだベクトルの和／差／スカラー倍の図形的なイメージを動画で紹介しています。ちょっと忘れてしまったかな、という方はぜひご視聴ください。

動画1　ベクトルの計算

print(a + b)  # リスト1で作成したa=(2, 3)とb=(4, 1)
print(a - b)
print(a * 2)
# 出力例：
# [6 4]  # aとbの対応する要素の和
# [-2  2]  # aとbの対応する要素の差
# [4 6]  # aの各要素を2倍

リスト2　ベクトルの和／差／スカラー倍を求める
+演算子や-演算子を使うと、対応する要素ごとの和や差を求めたベクトルが返される。*演算子を使ってスカラー倍すると、各要素をスカラー倍したベクトルが返される。

　*演算子を使ってベクトルをスカラー倍すると、ベクトルの各要素がスカラー倍されます。このように、1つの値と配列のそれぞれの要素との演算を行う機能をブロードキャスト機能と呼びます*2。

*2　実際には、ブロードキャスト機能は、1つの値と配列の演算だけでなく、行数と列数の異なる配列同士の演算の場合にも適用されます。そのような例については次回紹介します。

　ベクトルの各要素に対する割り算を行う場合には「1/除数」を掛けてもいいですが、割り算のための/演算子がそのまま使えます（リスト3）。整数商を求める//演算子、剰余を求める％演算子も使えます。

print(a / 2)  # リスト1で作成したa=(2, 3)
print(a // 2)
print(a % 2)
# 出力例：
# [1.  1.5]
# [1 1]
# [0 1]

リスト3　ベクトルの各要素をスカラーで割る
/演算子を使ってベクトルをスカラーで割ると、各要素の値をスカラーで割ったベクトルが返される。また、//演算子を使うと、各要素の値の整数商を要素としたベクトルが返される。

　それぞれの要素のべき乗を求める場合には、べき乗の演算子**がそのまま使えます（リスト4）。

print(a ** 2)  # リスト1で作成したa
# 出力例：
# [4 9]  # aの各要素を2乗

リスト4　ベクトルの各要素のべき乗を求める
**演算子を使ってベクトルのべき乗を求めると、各要素の値のべき乗を要素とするベクトルが返される。

　ちょっとした補足ですが、要素数が2個以上の異なるベクトルの和や差を求めようとしてもエラーになります。

import numpy as np

c = np.array([2, 3])
d = np.array([4, 1, 2])

print(c + d)
# 出力例：
# ---------------------------------------------------------------------------
# ValueError                                Traceback (most recent call last)
# <ipython-input-98-fb905072e5a3> in <module>()
#       2 c = np.array([2, 3])
#       3 d = np.array([4, 1, 2])
# ----> 4 print(c + d)
#
# ValueError: operands could not be broadcast together with shapes (2,) (3,)

リスト5　要素数の異なるベクトルの和／差を求めるとエラーになる
数学でもこのような計算はできないが、NumPyの配列でも要素数が異なるベクトルの和や差は求められない。ただし、要素数が1個の場合はスカラーと同様に計算される（例えば、cの要素が[2]のみである場合は、print(c + d)の結果は[6 3 4]となる）。

コラム　配列の次元とベクトルの次元

　ベクトルは1次元の配列で表すことができ、次回取り組む「行列」は2次元の配列で表すことができます（さらに、3次元以上の配列で表されるデータをテンソルと呼ぶこともあります）。

　ところで、配列を使いこなしている人でも、あまり意識していないかもしれませんが、配列の「次元」とベクトルの「次元」とは異なるものです。例えば、[2, 3]や[4, 1, 2]などの配列は1次元配列です。要素数はそれぞれ2つと3つですね。

　また、[[2, 3], [4, 1]]や[[2, 3, 5], [4, 1, 2]]といった配列は2次元配列です。[[2, 3, 5], [4, 1, 2]]であれば、3つの要素がある[2, 3, 5]と[4, 1, 2]という2つの配列を配列にしたものと考えられます。つまり配列が何重になっているかということが配列の次元です（図2）。

図2　1次元配列（上）と2次元配列（下）
配列の次元とは、配列が何重になっているかということ。［］の入れ子が何重になっているかと考えればよい。

　一方、ベクトルの次元は、1次元の配列の要素数で表されます。例えば、[2, 3]という配列で表されるベクトルは、2次元ベクトル（2次元空間の点）です。また、[4, 1, 2]なら、3次元ベクトル（3次元空間の点）を表します（図3）。

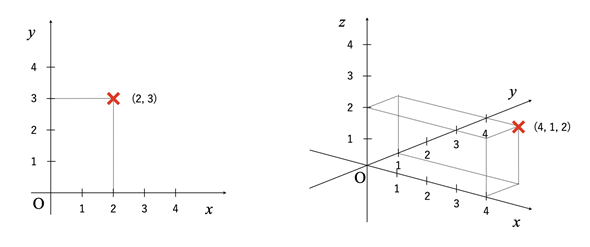図3　2次元ベクトル（左）と3次元ベクトル（右）
2次元ベクトルは1次元配列の2個の要素で表され、3次元ベクトルは1次元配列の3個の要素で表されることが分かる。2次元の図（左側）ではy軸が垂直方向に描かれているが、3次元の図（右側）ではz軸が垂直方向に描かれていることに注意。なお、右手の親指をx軸の向きに合わせ、人さし指をy軸の向きに合わせ、中指を親指と人さし指の両方に対して直角に立てるとz軸の向きと一致する。このような向きで座標を表す方法を「右手系の座標」と呼ぶことがある。

　つまり、n次元ベクトル（n次元空間の点の座標）は、n個の要素を持つ1次元配列で表されるということです。同じ「次元」という用語が使われますが、ベクトルや空間の次元と、配列の次元とは異なるものであることに注意してください。

コラム　リストに対して+、-、*、/、**の演算を行うと？

　Pythonのリストでも+や*という演算子が使えますが、NumPyの配列の場合とは意味が異なります。+演算子（リスト + リスト）はリストの連結という意味になり（リスト6）、*演算子（整数 * リスト、リスト * 整数）はリストの要素の繰り返しという意味になります（リスト7）。ただし、リストでは-、/、**という演算子は使えません。

lista = [2, 3]
listb = [4, 1]

print(lista + listb)
print(lista - listb)
# 出力例：
# [2, 3, 4, 1]
# ---------------------------------------------------------------------------
# TypeError                                 Traceback (most recent call last)
# <ipython-input-19-f5c2d1cda909> in <module>()
#       1 print(lista + listb)
# ----> 2 print(lista - listb)
#
# TypeError: unsupported operand type(s) for -: 'list' and 'list'

リスト6　リストでは+演算子は使えるが-演算子は使えない
リストの場合+演算子はリストの連結という意味になる。-演算子は使えないのでエラーとなる。

print(lista * 2)
print(lista ** 2)
# 出力例：
# [2, 3, 2, 3]
# ---------------------------------------------------------------------------
# TypeError                                 Traceback (most recent call last)
# <ipython-input-24-9c5f30115925> in <module>()
#       1 print(lista * 2)
# ----> 2 print(lista ** 2)
#
# TypeError: unsupported operand type(s) for ** or pow(): 'list' and 'int'

リスト7　リストでは*演算子は使えるが/演算子や**演算子は使えない
*演算子はリストの内容を何回か繰り返したものを返す。**演算子は使えないのでエラーとなる。上の例には示していないが/演算子も使えない。