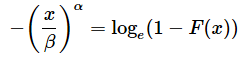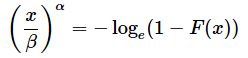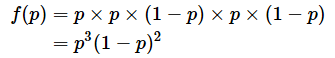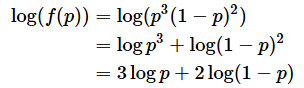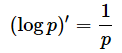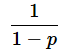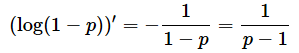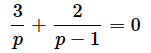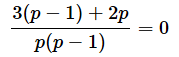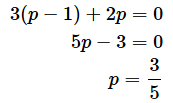［データ分析］ワイブル分布 〜 15年以内にエアコンが故障する確率は？：やさしい確率分布

データ分析の初歩から学んでいく連載（確率分布編）の第13回。ワイブル分布は機械の寿命や故障率の分析に使われる分布です。今回も具体例を基に、ワイブル分布の利用例や、確率密度関数と累積分布関数の形を見ていきます。母数（パラメーター）として指定するαやβの適切な値の決め方も解説します。

[羽山博，著]

連載目次

連載：

『社会人1年生から学ぶ、やさしい確率分布』

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』連載（記述統計と回帰分析編）の続編で、確率分布に焦点を当てています。
　この確率分布編では、推測統計の基礎となるさまざまな確率分布の特徴や応用例を説明します。身近に使える表計算ソフト（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムや統計ソフト「R」などでの作成例にも触れることにします。
　数学などの前提知識は特に問いません。中学・高校の教科書レベルの数式が登場するかもしれませんが、必要に応じて説明を付け加えるのでご心配なく。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。趣味の献血は心拍数が基準を超えてしまい99回で中断。心肺機能を高めるために水泳を始めるも、一向に上達せず。また、リターンライダーとして何十年ぶりかに大型バイクにまたがるも、やはり体力不足を痛感。足腰を鍛えるために最近は四股を踏む日々。超安全運転なので、原付やチャリに抜かされることもしばしば（すり抜けキケン、制限速度守ってね！）。

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の確率分布編、第13回（最終回）です。前回は、成功率の分布を求めたり、A/Bテストによる優劣を判定したりするのに使われるベータ分布を取り上げました。今回は機械などの寿命や故障率の分析に使われるワイブル分布の特徴や意味を基本から解き明かし、確率密度関数／累積分布関数の求め方、利用例などを見ていきます。

15年以内にエアコンが故障する確率を求める 〜 ワイブル分布の利用

　2024年の夏は記録的な猛暑でした。そんな中で、エアコンの故障という悲劇が筆者に襲いかかりました。冷房のボタンを押しても、暖房になってしまうのです！　調べてみると四方弁（しほうべん）と呼ばれる、冷房と暖房を切り替える弁が固着して動かなくなるのが原因のようでした。かなり古い機種だったので、修理ではなく買い換えを選択しましたが、今度は、新しいエアコンが猛暑のせいで上手く排熱できず、すぐに止まってしまうという事態に……。

　そんなわけで、私事からのお話でしたが、今回はエアコンの寿命について考えてみたいと思います（図1）。事例として取り上げるのはエアコンの寿命ですが、さまざまな機器や生命体の寿命などについても同様に応用できるお話です。

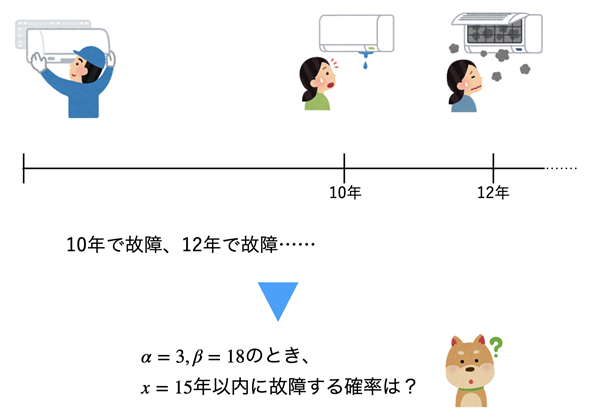図1　エアコンなどの機器が一定時間以内に故障する確率を求めたい！
故障するまでの年数のデータが何件かあるとき、ワイブル分布の母数α,βを求めて、x＝15年以内に故障する確率を求めたい。ただし、α,βの求め方については後述することとして、以下の例では、α＝3,β＝18で計算してみよう。

　すでに述べたように、機械の寿命などの分析にはワイブル分布が利用されます。ワイブル分布の母数は、分布の形を決める形状パラメーターαと分布の広がりを表すのに使われる尺度パラメーターβで、確率変数は時間を表すxとなります。

　ここでは、α＝3,β＝18であるものとして、x＝15年以内に故障する確率を計算するところから始めます。α,βが変わるとグラフの形がどう変わるのか、また、α,βをどうやって決めたのかが気になるところですが、それについては後述します。理屈は後回しにして、ExcelのWEIBULL.DIST関数を使って計算する方法を見ておきましょう。

　ここでは、Excelのヘルプに合わせて、形状パラメーターをα、尺度パラメーターをβという文字で表しています。ただし、文献によっては、形状パラメーターとしてmやβ、尺度パラメーターとしてαやη（イータ）などの文字が使われることがあります。α,βの意味が逆になっている場合もあるので、ご注意ください。

　WEIBULL.DIST関数の形式を見てから操作に進みます（図2）。

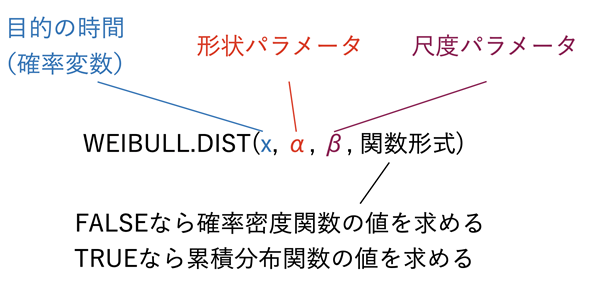図2　WEIBULL.DIST関数に指定する引数
WEIBULL.DIST関数には、確率変数x（目的の時間）と、形状パラメーターα、尺度パラメーターβを指定する。関数形式についてはこれまで見てきた関数と同様、FALSEを指定すれば確率密度関数の値が、TRUEを指定すれば累積分布関数の値が求められる。

　ワイブル分布の確率変数xには時間を指定します。累積分布関数では、指定した時間までに故障などの事象が起こる確率が求められます。ここでは故障を例としましたが、故障に限らず、目的の事象が起こるまでの時間が確率変数xとなるわけです。台（確率変数xが取り得る値の範囲）はloc〜∞です（locは指定した開始位置）。

　ExcelのWEIBULL.DIST関数では、locの値が0に固定されているので、x<0の場合はエラーになります。WEIBULL.DIST関数で台の開始位置を変えたい場合は、xからlocの値を引いてWEIBULL.DIST関数を適用します。

　では、ワイブル分布の母数をα＝3, β＝18として、累積確率を求めてみましょう。

　サンプルファイルをこちらからダウンロードし、［ワイブル分布の利用］ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］−［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。具体的な操作方法については、図中の説明を参照してください。

図3　WEIBULL.DIST関数の利用例
WEIBULL.DIST関数にはxの値、αの値、βの値を順に指定する。ここでは、15年以内に故障する確率を求めたいので、累積分布関数の値を求める。従って、最後の引数にはTRUEを指定する。

　図3のように、セルD4に「=WEIBULL.DIST(B4,B3,D3,TRUE)」と入力すると、セルD4の値は0.439（＝43.9％）となりました。15年以内に故障する確率は43.9％であるということが分かりました。

　続いて、ワイブル分布の確率密度関数と累積分布関数を可視化してみます。特に、累積分布関数を可視化すれば、何年か以内に故障する確率がよく分かります。が、その前に、ワイブル分布の確率密度関数と累積分布関数の定義だけを掲載しておきます。例によって、定義を覚える必要は全くありません。さらっとスルーして、ワイブル分布の可視化に進んでいただいて結構です。

ワイブル分布の確率密度関数と累積分布関数

　以下に示した式がワイブル分布の確率密度関数と累積分布関数の定義です。繰り返しになりますが、これらの式を覚える必要は全くありません。ExcelのWEIBULL.DIST関数を使えば、簡単に答えが求められます。

◆ ワイブル分布の確率密度関数

◆ ワイブル分布の累積分布関数

　ただし、eは自然対数の底（＝2.718...）です。

ワイブル分布ってどんな感じの分布（1） 〜 確率密度関数を可視化してみよう

　WEIBULL.DIST関数の引数として母数α,βに幾つかの値を指定し、xの値を変化させていったグラフを描けば、ワイブル分布の確率密度関数や累積分布関数を可視化できます。今回は、βについては図1の例で使った18という値を指定し、αの値を変えて可視化したいと思います。尺度パラメーターであるβを変えても分布の高さや幅が変わるだけですが、形状パラメーターであるαを変えるとグラフの形が変わるので、違いがよく分かると思います。

　なお、x＝0の場合、WEIBULL.DIST関数の値が0となり、グラフがきれいにつながらないことがあるので、x＝1〜50のグラフとします（図4）。

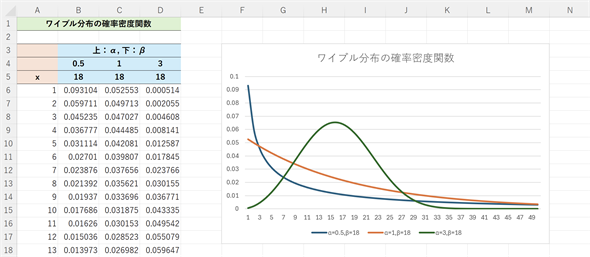図4　ワイブル分布の確率密度関数の例
αは0.5、1、3とし、βは18とする。x＝1〜50までの確率密度関数の値を1刻みで求めてグラフを描いてみた。xと表記されているA列の値が確率変数（横軸の値）。B〜D列の6行目以降はそれぞれのα,βでのxに対する確率密度関数の値。

　確率密度関数の値を求めるための手順は以下の通りです。可視化については単に折れ線グラフを描くだけなので、関数の入力にのみ焦点を当てることにします。グラフ作成の手順についてはサンプルファイル内に掲載しておきます。［ワイブル分布］ワークシートを開いて、図の後の手順で試してみてください。

◆ Excelでの操作方法

• セルB6に=WEIBULL.DIST(A6:A55,B4:D4,B5:D5,FALSE)と入力する
  • 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルB6〜D55）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す

◆ Googleスプレッドシートでの操作方法

• セルB6に=ARRAYFORMULA(WEIBULL.DIST(A6:A55,B4:D4,B5:D5,FALSE))と入力する

● グラフの作成方法

• サンプルファイル内に掲載しておきます（タイトルや軸の書式などの細かい設定は省略）

　図4のグラフを見ると、形状パラメーターαが1より小さいとき（例：α＝0.5）は、最初の部分（例えばx＝3まで）の値が大きく、徐々に落ち着いていくことが分かります。この場合は、初期不良のモデル化に使われます。形状パラメーターαが1のときは、λ＝1/βの指数分布となります。この場合は、一定の割合で（偶発的に）故障が起こるようなモデルとなります。形状パラメーターαが1より大きいとき（例：α＝3）は、徐々に故障が増えていく経年劣化のモデルとなります。このことは、図4のグラフよりも、故障率を可視化した図の方が分かりやすいので、後ほど掲載する図9であらためて見ることとします。

ワイブル分布ってどんな感じの分布（2） 〜 累積分布関数を可視化してみよう

　続いて、累積分布関数です。x,α,βの値は図4と同様とします（図5）。［ワイブル分布累積］ワークシートを開いて、図の後の手順で試してみてください。

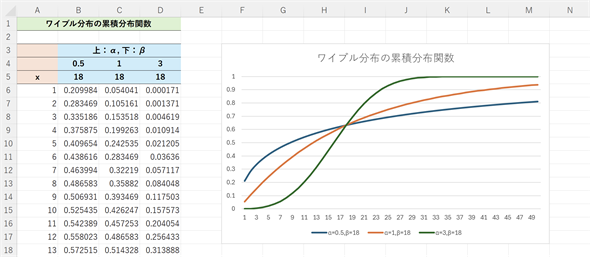図5　ワイブル分布の累積分布関数の例
図4と同様、αは0.5、1、3とし、βは18とする。x＝1〜50までの累積分布関数の値を1刻みで求めてグラフを描いてみた。xと表記されているA列の値が確率変数（横軸の値）。B〜D列の6行目以降はそれぞれのα,βでのxに対する累積分布関数の値。

　操作の手順は図4とほぼ同じです。違いは、WEIBULL.DIST関数の［関数形式］に累積分布関数を表すTRUEを指定することだけです。図4の場合と同様、グラフ作成の手順についてはサンプルファイル内に掲載しておきます。

◆ Excelでの操作方法

• セルB6に=WEIBULL.DIST(A6:A55,B4:D4,B5:D5,TRUE)と入力する
  • 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルB6〜D55）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す

◆ Googleスプレッドシートでの操作方法

• セルB6に=ARRAYFORMULA(WEIBULL.DIST(A6:A55,B4:D4,B5:D5,TRUE))と入力する

● グラフの作成方法

• サンプルファイル内に掲載しておきます（タイトルや軸の書式などの細かい設定は省略）

　図5のグラフから、α＝3,β＝18の場合は、x＝30あたりで累積確率がほぼ1に近づくことが分かります。つまり、最初の図1で見たエアコンは、長く使えたとしても30年程度でほぼ寿命が来るものと考えてよさそうです。寿命を求めるには、次の項で見るワイブル分布の逆関数が便利です。

故障する確率が95％となる時間を求める 〜 ワイブル分布の逆関数

　ワイブル分布の累積分布関数は、ある時間までに故障する確率を求めるのに使えます。ということは、その逆関数を利用すれば、故障する累積確率が何％かになる時間を求めることができます。例えば、故障する確率が95％以上になる時間が求められます。

　しかし、Excelにはワイブル分布の逆関数を求めるための関数がありません。そこで、累積分布関数の値を求める（2）式をxについて解いた式を使います。（2）式は以下の通りでした。

　これをxについて解くと、以下のようになります（解き方については、後のコラムで解説します）。対数logは底がeの自然対数です。

　では、（3）式を使って、故障する累積確率F(x)の値が95％以上になる時間を求めてみましょう。自然対数はLN関数で求められるので、図6のようになります。［ワイブル分布の逆関数］ワークシートを開いて試してみてください。

図6　ワイブル分布の累積分布関数に対する逆関数を利用する
累積確率F(x)の値はセルB4の95％、αに当たるのがセルB3の値、βに当たるのがセルD3の値。

　セルD4に（3）式の計算を行う数式（＝「=D3*(-LN(1-B4))^(1/B3)」）を入力すると、25.95という値が得られます。これは、ほぼ26年を過ぎると故障率が95％以上になることを意味します。

コラム　ワイブル分布の逆関数を自作する

　ExcelのLAMBDA関数と名前機能を使うと、関数が自作できます。そこで、ワイブル分布の累積分布関数に対する逆関数の値を求めるWEIBULL.INV関数を自作してみましょう。操作方法は図7に示した通りです。［ワイブル分布の逆関数］ワークシートを開いて試してみてください。なお、LAMBDA関数はMicrosoft 365のExcelやデスクトップ版のExcel 2021以降でサポートされており、Excel 2019以前のバージョンでは利用できません。

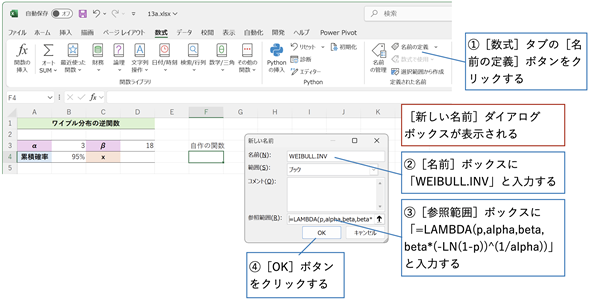図7　ワイブル分布の累積分布関数に対する逆関数を自作する
LAMBDA関数を使って自作の関数を作成し、分かりやすい名前を付けておけばよい。ここでは、［範囲］を「ブック」としているが、特定のワークシートだけで使う関数であれば、［範囲］の一覧からワークシート名を選択すればよい。なお、［ワイブル分布の逆関数（完成例）］ワークシートではWEIBULL.INV関数をワークシート内だけで使えるものとして定義してある。

　LAMBDA関数は、この連載の記述統計編第16回でも取り上げました。上の例に則して簡単に解説しておきます（図8）。

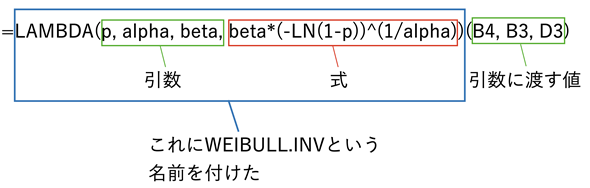図8　LAMBDA関数の使い方
LAMBDA関数の定義には「引数」と「式」を指定する。引数には分かりやすい名前を付けておけばよい。指定した引数を使って「式」の計算を行うという意味になる。実際に計算するときには、定義の後に()に囲んで指定した値が順に、引数に渡される。この例であれば、セルB4の参照がpに、セルB3の参照がalphaに、セルD3の参照がbetaに渡される。図7では名前機能を使って、LAMBDA関数の定義にWEIBULL.INVという名前を付けているので、=WEIBULL.INV(B4,B3,D3)と入力すれば「式」の計算ができる。

　LAMBDA関数を使えば、式の中で使われる引数（変数）と、式を記述するだけで、新しい関数が作成できます。さらに、名前機能を使って分かりやすい名前を付けておけば、自作関数の出来上がりです。自作の関数が作成できたら、空いているセルに=WEIBULL.INV(B4,B3,D3)と入力してみてください。図6と同じ25.94818...という結果が得られます。

　なお、Googleスプレッドシートでは、名前付き関数の機能を使って同じことができます。ただし、名前付き関数では関数名に「.」が使えないので、サンプルファイルでは「WEIBULL_INV」という名前にしてあります。名前付き関数の作り方はサンプルファイル内に記しておきます。

コラム　ワイブル分布の逆関数を求める

　図6で使ったワイブル分布の累積分布関数に対する逆関数の式は、以下のようにして求めます。単に数式を変形しているだけなので、数式が苦手な方はスルーしてもらっても構いません。

　累積分布関数F(x)は以下の通りでした。

　（2）式のF(x)を右辺に、

を左辺に移項します。

　両辺の自然対数を求めると以下のようになります。

　対数の公式log_ee^a ＝ aを適用すると、左辺の指数部分が取り出せます。

　両辺に−1を掛けて、

　両辺を1/α乗すると、以下のようになります。

　両辺にβを掛ければ、（3）式となります。

故障率を求めてバスタブ曲線を確認する

　すでに述べたように、ワイブル分布は形状パラメーターαの値を変えることによって、以下のようなモデルの記述に使われます。

• α < 1　……　初期不良のモデル
• α ＝ 1　……　偶発的な故障のモデル（指数分布）
• α > 1　……　経年劣化のモデル

　故障率を可視化してこのことを確認してみましょう。故障率は以下の式で求められます。

　ここでは、バスタブ曲線と呼ばれるグラフのイメージが分かるように、αとβにやや極端な値を指定した例を見てみます（図9）。［故障率］ワークシートを開いて試してみてください。操作方法は図9の後に記しておきます。

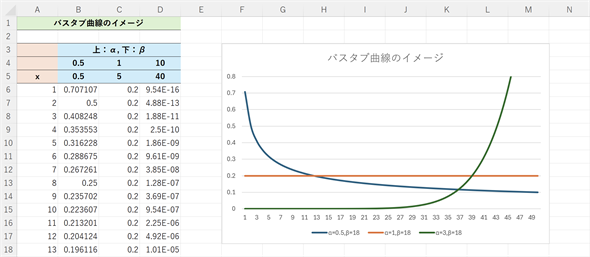図9　バスタブ曲線のイメージ
α<1の場合、グラフの左側に見られるような初期不良の故障率が可視化できる。、α＝1の場合、グラフの中央付近で見られるような一定の故障率（偶発的な故障の率）となる。alpha>1の場合、グラフの右端で見られるように、時間とともに故障率が増えていく。これは経年劣化を表しているものと考えられる。全体ではバスタブ（浴槽）のような形になっていることが分かる。

◆ Excelでの操作方法

• セルB6に=B4:D4/B5:D5*(A6:A55/B5:D5)^(B4:D4-1)と入力する
  • 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルB6〜D55）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す

◆ Googleスプレッドシートでの操作方法

• セルB6に=ARRAYFORMULA(B4:D4/B5:D5*(A6:A55/B5:D5)^(B4:D4-1))と入力する

● グラフの作成方法

• サンプルファイル内に掲載しておきます（タイトルや軸の書式などの細かい設定は省略）

　セルB6に入力する=B4:D4/B5:D5*(A6:A55/B5:D5)^(B4:D4-1)という式はスピル機能にかなり慣れていないと分かりにくいかもしれません。取りあえず、（4）式に従って、セルB6に数式を素直に入力するなら=B4/B5*(A6/B5)^(B4-1)となります。αがセルB4に、βがセルB5に、xがセルA6に当たるので、（4）式そのままですね。ただし、この式ではセルB6の値しか求められません。そこで、全ての値を一度に求めるために、αとしてB4:D5を、βとしてB5:D5を、xとしてA6:A55を指定したわけです。

　図9に示されたバスタブのような形のグラフでは、故障率が時間とともにどのように変化するかが示されています。α<1の場合は「初期不良」を表し、グラフの左側で故障率が高くなることが分かります。一方、α＝1の場合は故障率が一定となり、「偶発的な故障」が起こる率を示しています。α>1の場合は「経年劣化」が進み、時間の経過とともに故障率が増加する様子が右側に表れています。

形状パラメーターαと尺度パラメーターβの推定

　ここまでは、ワイブル分布を利用して故障の確率や故障率を求めてきました。計算の方法は分かったと思いますが、αやβをどうやって決めるのか、という問題が残っています。これらの母数を推定する方法は、推測統計編の話題になるのですが、簡単に紹介しておきます。

　母数を推定するためには、測定されたサンプルの値を使います。その方法には、最尤（さいゆう）推定法や最小二乗法（回帰分析）による推定法などがあります。

　最尤推定法とは、サンプルを基に、母数として「最も尤もらしい」（もっとも、もっともらしい）値を推定する方法です。簡単に言うと、各試行の確率の積を母数の関数（尤度関数、「ゆうどかんすう」と読む）とし、その関数を最大にする母数の推定値を求めるというものです。ただし、積（掛け算）の形だと、微分などの計算が面倒なので、和（足し算）にするために対数を取った対数尤度関数を求め、対数尤度関数を最大にする母数の推定値を求めるのが普通です。後のコラムで簡単な例を紹介します。

　Excelではいずれの方法もかなりの手間がかかるので、ここでは、Pythonのプログラムを使って、最尤推定法による母数の推定を行ってみましょう。

　サンプルプログラムはこちらから参照できます。リンクをクリックすれば、ブラウザが起動し、Google Colaboratoryの画面が表示されます（Googleアカウントでのログインが必要です）。最初のコードセルをクリックし、［Shift］+［Enter］キーを押してコードを実行してみてください。コードの詳細については解説しませんが、コード内のコメントとリスト1の説明を見れば何をやっているかが大体分かると思います。

from scipy.stats import weibull_min

# 故障した年数
data = [5, 10, 13, 13, 16, 17, 18, 21, 23, 26]

# 母数の推定
shape, loc, scale = weibull_min.fit(data, floc=0)
print(shape, scale)

# 出力例
3.0420091560120834 18.139000902259845

リスト1　最尤法によりワイブル分布の母数を推定する
scipy.statsモジュールのweibull_minは、故障時間や寿命などの分析に使われるクラス。fit関数にデータを指定すれば、形状パラメーターα、分布の開始位置、尺度パラメーターβの推定値が求められる。floc=0は分布の開始位置を0に固定するという意味。ここでは、形状パラメーターと尺度パラメーターのみを表示した。

　結果は形状パラメーターの推定値が3.04、尺度パラメーターの推定値が18.14となっています。最初に示した事例でα＝3、β＝18としたのは、このようなデータから推定された母数を想定したものだったから、というわけです。

　なお、上記のサンプルプログラムのノートブックファイルには、最小二乗法により母数の推定を行った例も含めてあります。ただし、サンプル数が少ない場合は最尤推定法との違いが大きくなるので、1000個のサンプルデータとしてあります。Google Colaboratoryの2つ目のコードセルをクリックし、［Shift］+［Enter］キーを押して実行すると、回帰分析による推定と最尤推定法の結果を比較できます（ほぼ同じ値になります）。

　参考として、Excelでの最尤推定法による母数の推定と最小二乗法による母数の推定を行った例も、Excelのサンプルファイルに含めてあります。ただし、最尤推定法の場合は、対数尤度関数を最大化する母数を求めるために、あらかじめソルバーアドインを組み込んでおく必要があります。詳細については割愛しますが、サンプルファイル中に簡単な説明を掲載しています。

コラム　最尤推定法のごく簡単な例

　最尤推定法がどのようなものであるか、実感が湧かないかもしれないので、ここでは、できるだけ簡単な例としてベルヌーイ試行を取り上げ、最尤推定法による母数の推定を手計算でやってみたいと思います。例えば、コインを投げて、表が出たことを1、裏が出たことを0と表すものとして、5回の試行が[1, 1, 0, 1, 0]という結果になったとします。

　ベルヌーイ分布の母数p（表が出る確率）を最尤推定してみます。表が出る確率はp、裏が出る確率は1−pです。最初に出た「1」という値が現れる確率として「もっともらしい」と考えられる値は、pですね。この値を「尤度（ゆうど）」と呼びます。次に出た「1」の尤度もpです、その次に出た「0」の尤度は1−pですね。このようにして求めた全ての試行の尤度（確率）を掛け合わせ、それを関数（尤度関数）と見なして、f(p)と表すと、

となります。この尤度関数の値を最大にするpの値を母数の推定値とします。この例は簡単なので、このままでも0<p<1の範囲でf(p)を最大化するpの値を求めることはできますが、普通は対数を取った対数尤度関数とします。

　この関数は0<p<1の範囲で上に凸となっているので、最大値を持ちます。そこで、微分して0と置きます。

　対数関数の微分の公式

を適用して、左辺を変形すると、以下のようになります。ただし、log(1−p)の微分は、

ではありません。1−pをuと置いて合成関数の微分を行う必要があります。計算の過程は省略しますが、結果は、

となります。従って、（5）式は、以下のようになります。

　0<p<1なので、分母が0にならないことも確認できますね。通分すると、

となるので、両辺にp(p−1)を掛けて、

となります。結局のところ、5回のうち3回表が出たので、表が出る確率pの最尤推定値は3/5で求められますが、最尤推定法による母数の推定を手計算でやるとこのようになるというわけです。

---

　今回はワイブル分布について、簡単な利用例を紹介した後、確率密度関数と累積分布関数の求め方についてお話しし、さらに、推測統計の領域に少し踏み込んで、母数の推定方法も紹介しました。

　さて、離散型確率分布の二項分布から始まったこの連載も、超幾何分布やポアソン分布、連続型確率分布の代表とも言える正規分布、さらには、カイ二乗分布、t分布、F分布、ベイズ統計などでよく使われるベータ分布を経て、今回で最終回となりました。

　この連載では、確率分布の利用例を紹介する中で、必要に応じて推測統計についても個別に説明しました。しかし、具体的な事例の紹介や体系的な解説はしていません。そこで、この連載の続編として『社会人1年生から学ぶ、やさしい推測統計』で、推測統計についての詳しい解説を準備しています。どうぞお楽しみに！

この記事で取り上げた関数の形式

　関数の利用例については、この記事の中で紹介している通りです。ここでは、今回取り上げた関数の基本的な機能と引数の指定方法だけを示しておきます。

ワイブル分布の確率密度関数や累積分布関数の値を求めるための関数

WEIBULL.DIST関数： ワイブル分布の確率密度関数や累積分布関数の値を求める

形式

WEIBULL.DIST(x, α, β, 関数形式)

引数

• x： 故障するまでの時間などを指定する。
• α： 形状パラメーターを指定する。
• β： 尺度パラメーターを指定する。
• 関数形式： 以下の値を指定する。
  • FALSE …… 確率密度関数の値を求める
  • TRUE …… 累積分布関数の値を求める

LN関数： 自然対数の値を求めるための関数

形式

LN(x)

引数

• x： 自然対数を計算する際の対象となる数値（真数）を指定する。

LAMBDA関数： 独自の関数を作るための関数

形式

LAMBDA(引数1, 引数2, ..., 式)

引数

• 引数1, 引数2, ...： 式に与える引数に対応する変数名を定義する。
• 式： 変数を使った計算の方法を指定する。

備考

　例えば、「=LAMBDA(x, y, x+y)」であれば、最初のxに第1引数の値が渡され、yに第2引数の値が渡される。最後のx+yの値が答えとして返される。従って、セルに「=LAMBDA(x, y, x+y)(A1,A2)」と入力すると、セルA1の値がxに渡され、セルA2の値がyに渡され、x+yの値つまりA1とA2の和が返される。さらに、名前機能を利用して「=LAMBDA(x, y, x+y)」にmyaddといった名前を付ければ、「=myadd(A1, A2)」でセルA1とセルA2の和が求められる。このようにして関数を自作できる。

　なお、LAMBDA関数は、Excel 2019以前では使えない。

「やさしい確率分布」

AI・データサイエンスの学びをここから

初心者向け、データ分析・AI・機械学習・Pythonの勉強方法　＠ITのDeep Insiderで学ぼう