[データ分析]ガンマ分布とアーラン分布 〜 5分以内に2匹以上の猫が通る確率は?:やさしい確率分布
データ分析の初歩から学んでいく連載(確率分布編)の第11回。ガンマ分布やアーラン分布は、待ち行列の分析などに使われる分布です。ある事象が起こる平均の間隔が分かっているときに、ある期間内にその事象が何回か以上起こる確率が求められます。今回は具体例を基に、その確率を求め、ガンマ分布の確率密度関数や累積分布関数の形を見ていきます。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
連載:
この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』連載(記述統計と回帰分析編)の続編で、確率分布に焦点を当てています。
この確率分布編では、推測統計の基礎となるさまざまな確率分布の特徴や応用例を説明します。身近に使える表計算ソフト(Microsoft ExcelやGoogleスプレッドシート)を使いながら具体的に事例を見ていきます。
必要に応じて、Pythonのプログラムでの作成例にも触れることにします。
数学などの前提知識は特に問いません。中学・高校の教科書レベルの数式が登場するかもしれませんが、必要に応じて説明を付け加えるのでご心配なく。肩の力を抜いてぜひとも気楽に読み進めてください。
筆者紹介: IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。趣味の献血は心拍数が基準を超えてしまい99回で中断。心肺機能を高めるために水泳を始めるも、一向に上達せず。また、リターンライダーとして何十年ぶりかに大型バイクにまたがるも、やはり体力不足を痛感。足腰を鍛えるために最近は四股を踏む日々。超安全運転なので、原付やチャリに抜かされることもしばしば(すり抜けキケン、制限速度守ってね!)。
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の確率分布編、第11回です。前回は、待ち行列の分析などに使われる指数分布を取り上げました。今回も同様に待ち行列の分析などに使われるガンマ分布について、その特徴や意味を基本から解き明かし、確率密度関数/累積分布関数の求め方、利用例などを見ていきます。
一定時間内に何匹か以上の猫が通る確率は? 〜 ガンマ分布とアーラン分布の利用
ガンマ分布は、ある事象(出来事)が起こる平均の間隔βが分かっているときに、ある期間x内にその事象がα回以上起こる確率を表す分布です。ガンマ分布の母数αが正の整数である場合は、特にアーラン分布と呼ばれます。
少し前のことですが、筆者の仕事場の前が野良猫の通り道になっていて、仕事をしているとよく猫が目の前を横切りました。このことを例に、ガンマ分布がどのように適用できるか、具体例を見てみましょう(図1)。
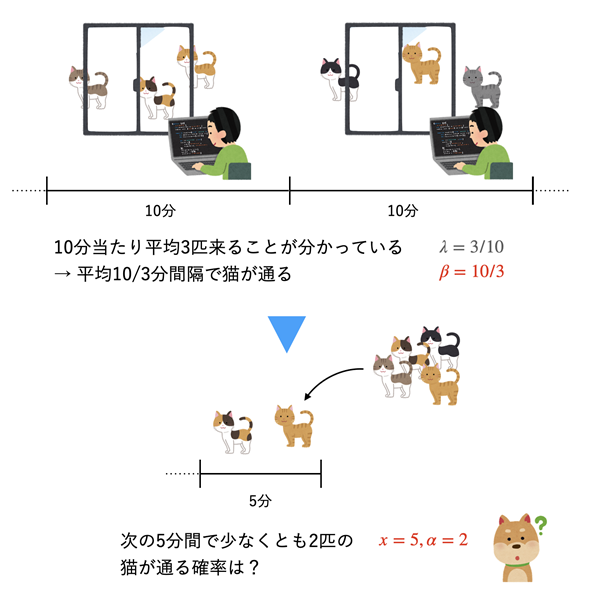 図1 ある期間に何匹か以上の猫が通る確率を知りたい!
図1 ある期間に何匹か以上の猫が通る確率を知りたい!ガンマ分布の累積分布関数は、事象が起こる平均の間隔βが分かっているとき、目的の期間x内にその事象が少なくともα回起こる(=α回以上起こる)確率を求めるのに使う。
図1に示された問題意識は、10分当たり平均3匹の猫が通ることが分かっている場合に、次の5分間に少なくとも2匹の猫が通る(2匹以上の猫が通る)確率を求めたい、ということです。そんなことをして何の役に立つのか、と思われるかもしれませんが、「猫」を「顧客」や「車」に置き換えると、一定時間内に何人かの顧客が到着する確率や一定時間内に車が何台か以上通る確率を求めるということになり、がぜん、実用性が感じられるようになると思います(車の通行量の例についても、後ほど見ることにします)。
ところで、図1で「猫」を「顧客」に置き換えると、前回見た指数分布とそっくりですね。でも違いがあります。まずは指数分布との違いを確認するところから始めましょう。
指数分布とガンマ分布との違いを具体的かつ端的に言うと、指数分布の累積分布関数は、ある期間内に少なくとも1回の事象が起こる(1回以上起こる)確率を求めるのに使いますが、ガンマ分布の累積分布関数は、ある期間内に少なくともα回の事象が起こる(α回以上起こる)確率を求めるために使われます。
ガンマ分布でα=1の場合、指数分布になります。また、ガンマ分布は、独立した指数分布の和と考えられます。具体的にどういうことなのかは、最後のコラムで解説します。
ガンマ分布の母数はαとβで、指数分布の母数はλです。これらを表にまとめて比較してみます(表1)。いずれも確率変数は目的の期間です。
| ガンマ分布 | 指数分布 | ||
|---|---|---|---|
| 母数 | 目的の期間内で事象が何回以上起こるか | α | - |
| 一定期間内で事象が起こる平均の間隔 | β | - | |
| 一定期間内で事象が起こる平均の回数 | - | λ | |
| 確率変数 | 目的の期間 | x | x |
-は指定する必要がないことを意味する。図1の例であれば、事象は「猫が通ること」に当たる。従って「目的の期間内に事象が何回以上起こるか」は「目的の時間内に猫が何匹以上通るか」と読み替えられる。これがαの値となる。図1の例であればα=2。また、「一定期間内で事象が起こる平均の間隔」は「猫が通る平均の時間間隔」となる。これがβの値。図1の例なら10/3(分)。
指数分布の母数λは「一定期間内で事象が起こる回数」です。一方、ガンマ分布の母数βは「一定期間内で事象が起こる平均の間隔」なので、λの逆数となります。つまり、β=1/λとなります。例えば、10分間に3匹の猫が通るのであれば、λ=3/10です。この場合、
となります。10分間に3匹の猫が通るということは、平均して10/3分間に1匹の猫が通るということですね。
指数分布と比較しながらガンマ分布の意味が確認できたので、ガンマ分布の確率密度関数と累積分布関数の定義を見た後、図1の確率を計算してみましょう。
ガンマ分布の確率密度関数と累積分布関数
以下に示した式がガンマ分布の確率密度関数と累積分布関数の定義です。eは自然対数の底(=2.71828...)です。かなり複雑な式ですが、例によって、これらの式を覚える必要は全くありません。ExcelのGAMMA.DIST関数を使えば、簡単に答えが求められます。
◆ ガンマ分布の確率密度関数
◆ ガンマ分布の累積分布関数
ただし、Γはガンマ関数、γは下側不完全ガンマ関数(第一種不完全ガンマ関数)です。これらの関数の定義は、第7回のコラムで紹介しました(繰り返しになりますが、それらの定義を覚えたりする必要はありません)。
GAMMA.DIST関数の書き方は以下の通りです。
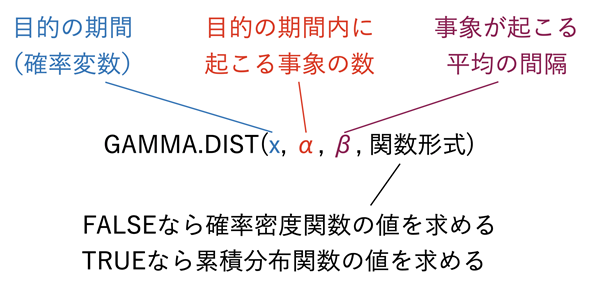 図2 GAMMA.DIST関数に指定する引数
図2 GAMMA.DIST関数に指定する引数GAMMA.DIST関数には、目的の期間xと、何回以上その事象が起こるかを表すα、事象が起こる平均の間隔βを指定する(βは、あらかじめ分かっている値)。関数形式についてはこれまで見てきた関数と同様、FALSEを指定すれば確率密度関数の値が、TRUEを指定すれば累積分布関数の値が求められる。
冒頭の図1で紹介した例について、GAMMA.DIST関数を使って確率を求めてみましょう。10分間に平均して3匹の猫が通る=平均して10/3分間に1匹の猫が通ることが分かっている場合に、次の5分以内に2匹以上の猫が通る確率を求めます。この場合、確率変数xの値は5で、α=2,β=10/3となります。
サンプルファイルをこちらからダウンロードし、[ガンマ分布の利用]ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。
 図3 GAMMA.DIST関数の利用例
図3 GAMMA.DIST関数の利用例GAMMA.DIST関数にはxの値、αの値、βの値を順に指定する。ここでは累積分布関数の値を求めるので、最後の引数にはTRUEを指定する。よってセルB7に=GAMMA.DIST(B5,B3,B4,TRUE)と入力すればよい。猫が通る平均の時間間隔がβ=10/3分であるとき、x=5分以内にα=2匹以上の猫が通る確率は0.442であることが分かる。
私たちは、無意識のうちに「期間」を分単位や年単位などで考えてしまいます。例えば、10分であれば、期間は10であると考えるのが普通です。しかし、ここでの期間とは一定の間隔のことです。問題に合わせて、例えば、10分を1つの期間と考えたり、100年を1つの期間と考えたりしても構いません。例えば、上の例で10分を1つの期間と考えれば、1つの期間に猫が3匹通ることになります。その場合、λ=3なので、β=1/3となります。目的の間隔は5分なので、1つの期間とした10分の半分、つまり1/2がxの値となります。αについては2のままですね。空いているセルに「=GAMMA.DIST(1/2, 2, 1/3, TRUE)」と入力してみてください。図3の結果と一致します。
続いて、ガンマ分布の確率密度関数と累積分布関数を可視化してみましょう。
ガンマ分布ってどんな感じの分布(1) 〜 確率密度関数を可視化してみよう
上で見たGAMMA.DIST関数の引数として母数α,βに幾つかの値を指定し、xの値を変化させていったグラフを描けば、ガンマ分布の確率密度関数や累積分布関数を可視化できます。ただし、以下の例ではβ=3に固定するものとします。ガンマ分布の台(確率変数が取り得る値の範囲)は0〜∞ですが、α=1, x=0のときにはGAMMA.DIST関数がエラーとなるので、ここではx=1〜30までの値を求めることとします(図4)。
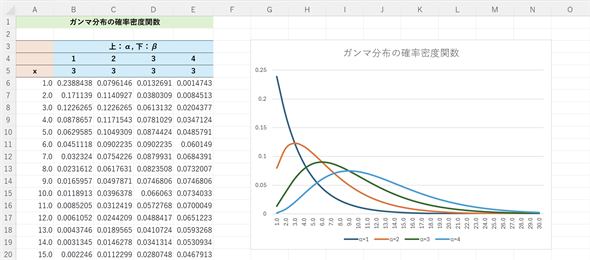 図4 ガンマ分布の確率密度関数の例
図4 ガンマ分布の確率密度関数の例αは1, 2, 3, 4とし、βは3に固定。x=1.0〜30.0までの確率密度関数の値を1刻みで求めてグラフを描いてみた。xと表記されているA列の値が確率変数(確率変数は整数でなくてもよい)。B〜E列の6行目以降はそれぞれのα,βでのxに対する確率密度関数の値。
確率密度関数の値を求めるための手順は以下の通りです。サンプルファイルの[ガンマ分布]ワークシートを開いて試してみてください。可視化については単に折れ線グラフを描くだけなので、関数の入力のみに焦点を当てることにします。グラフ作成の手順についてはサンプルファイル内に掲載しておきます。
◆ Excelでの操作方法
- セルB6に=GAMMA.DIST(A6:A35,B4:E4,B5:E5,FALSE)と入力する
- 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲(セルB6〜E35)をあらかじめ選択しておき、関数を入力した後、入力の終了時に[Ctrl]+[Shift]+[Enter]キーを押す
◆ Googleスプレッドシートでの操作方法
- セルB6に=ARRAYFORMULA(GAMMA.DIST(A6:A35,B4:E4,B5:E5,FALSE))と入力する
● グラフの作成方法
- サンプルファイル内に掲載しておきます(タイトルや軸の書式などの細かい設定は省略)
ガンマ分布ってどんな感じの分布(2) 〜 累積分布関数を可視化してみよう
続いて、累積分布関数です。こちらは、α=2,β=3の例だけを見ておきます(図5)。[ガンマ分布累積]ワークシートを開いて、図の後の手順で試してみてください。
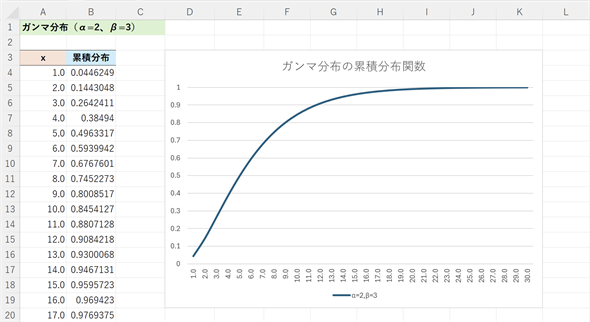 図5 ガンマ分布の累積分布関数の例
図5 ガンマ分布の累積分布関数の例αを2、βを3として、x=1.0〜30.0までの累積分布関数の値を1刻みで求めてグラフを描いてみた。x=20になると累積確率は99%を超える。例えば、猫が通る間隔が平均3分であるとき、20分以内にはほぼ確実に2匹(以上)の猫が通ることが分かる。
累積分布関数の値を求めるための手順は以下の通りです。ここでも、関数の入力のみに焦点を当てることとし、グラフ作成の手順についてはサンプルファイル内に掲載しておきます。
◆ Excelでの操作方法
- セルB4に=GAMMA.DIST(A4:A33,2,3,TRUE)と入力する
- 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲(セルB4〜B33)をあらかじめ選択しておき、関数を入力した後、入力の終了時に[Ctrl]+[Shift]+[Enter]キーを押す
◆ Googleスプレッドシートでの操作方法
- セルB4に=ARRAYFORMULA(GAMMA.DIST(A4:A33,2,3,TRUE))と入力する
● グラフの作成方法
- サンプルファイル内に掲載しておきます(タイトルや軸の書式などの細かい設定は省略)
ガンマ分布も指数分布と同様、確率変数を求めるための計算などがなく、また、累積分布関数が直接応用に結び付くので、比較的すんなりと理解できるのではないかと思います。ここからは、少し発展的なお話としてガンマ分布とポアソン分布との関係を見てみます。また、ガンマ分布が指数分布の和であるということをシミュレーションで確認します。実用的には知らなくてもあまり問題がないので、数式が苦手な方や変数の対応関係を細かく確認するのが面倒だと思われる方は、最後の「この記事で取り上げた関数の形式」を確認して、今回はお開きとしてもらっても構いません。
コラム ガンマ分布と指数分布、ポアソン分布の関係
前回、指数分布とポアソン分布の関係をコラムで解説しました。ガンマ分布は指数分布の和である(詳細は次のコラムで見ます)ということなので、ガンマ分布と指数分布、ポアソン分布が互いに関係しているということも想像できると思います。そこで、それらの関係を図で表し、その後、もう一度意味を考えていくことにします。
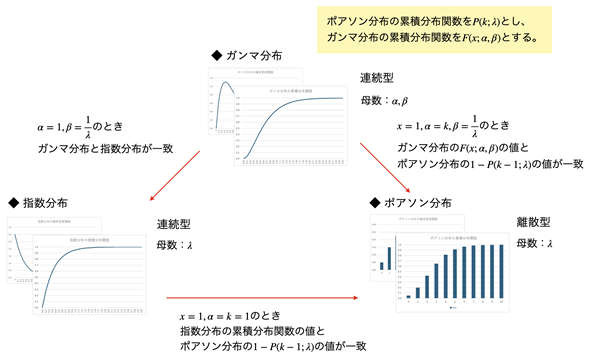 図6 ガンマ分布と指数分布、ポアソン分布の関係
図6 ガンマ分布と指数分布、ポアソン分布の関係α=1, β=1/λのとき、ガンマ分布と指数分布は一致する。また、ポアソン分布の累積分布関数をP(k;λ)とし、x=1,α=k,β=1/λとしたとき、ガンマ分布の累積分布関数F(x,α,β)は、1−P(k−1;λ)と一致する。詳細についてはこの後解説する。
ガンマ分布の累積分布関数とポアソン分布の累積分布関数の違いを端的に言うなら、以下のようになります。
- ガンマ分布の母数βは一定期間内に事象が起こる平均の間隔であるが、ポアソン分布の母数λは一定期間内に事象が起こる回数(いずれもあらかじめ分かっている値) …… 従って、β=1/λとなる
- ガンマ分布では目的の期間が確率変数xとなるが、ポアソン分布では事象が起こる期間(あらかじめ分かっている期間)と目的の期間は同じなので、式の中には現れない …… ガンマ分布でx=1とすると、ポアソン分布の期間と同じになる
- ガンマ分布の累積分布関数では、目的の期間に事象がα回以上起こる確率が求められるのに対し、ポアソン分布の累積分布関数では、目的の期間に事象がk回まで起こる確率が求められる。
これらの関係を数式で解き明かすのはかなり難しいので、ここでは、図6や上に示した箇条書きの意味を具体的な例で考えてみましょう。猫の事例よりも実用的な例として、車の通行量で考えることにします(さらに言えば、コールセンターに入る電話の数や機器の故障の数などでも基本的な考え方は同じです)。理屈よりも実際に計算した例を先に見たいという方は、こちらまで読み飛ばしていただいても構いません。
離散型確率分布であるポアソン分布が分かりやすいので、ポアソン分布を中心に見ていくことにしましょう。以下、母数λの表記は省略して、ポアソン分布の確率質量関数をp(k)、累積分布関数をP(k)と簡単に表すことにします。例えば、1分間に平均してλ=3台の車が通ることが分かっている場合、1分間に車が、
- k=5台通る確率は、確率質量関数p(k=5)の値 …… (1)
- k=5台まで通る確率は、累積分布関数P(k=5)の値 …… (2)
で求められます。従って、1分間に車が
- k=5台以上通る確率は1−P(k−1=4)の値 …… (3)
となります(全体からk−1台まで通る確率を引けばよい)。
一方、ガンマ分布の累積分布関数では、車が通る平均の間隔をβとするので、β=1/λ=1/3です。
- 期間x内に車がα=5台以上通る確率は、累積分布関数F(x;α,β)の値
ということは、ガンマ分布でx=1, α=k, β=1/λとしたときの累積分布関数の値F(1; α, β)と、ポアソン分布での(3)の計算、つまり1−P(k−1)の値が同じになるはずです。
また、指数分布の累積分布関数の値は、ガンマ分布でα=1, β=1/λを指定した場合の累積分布関数の値や、ポアソン分布でk=1を指定した場合の1−P(k−1)の値と同じになります。
では、具体的な値を当てはめて確認してみましょう。[分布同士の関係]ワークシートを開いて、以下のように入力すると同じ結果が得られることが分かります。
 図7 ガンマ分布と指数分布、ポアソン分布の関係を確認する
図7 ガンマ分布と指数分布、ポアソン分布の関係を確認するセルB8のPOISSON.DIST関数では、ポアソン分布のk−1に当たる値としてB4-1を指定して累積分布関数の値を求めている(k−1回までの確率が求められる)。
セルC8では1からその値を引いて、事象がk回以上起こる確率を求める。
一方、セルD8のGAMMA.DIST関数では、時間間隔xに当たる値としてセルB5を指定し、αに当たる値としてセルB4を、β=1/λに当たる値として1/B3を指定している。この場合、セルB5に1を入力すると、x=1となるので、セルC8とセルD8の値が一致する。
さらに、セルB4の値が1のとき、k=α=1なので、セルC8、D8の値とセルE8のEXPON.DIST関数の値が一致する(セルB4に1を入力して試してみるとよい)。
セルB5に入力されたxの値が1であれば、ポアソン分布の1−P(k−1)の値に当たるセルC8の値と、ガンマ分布のF(x;α,β)の値に当たるセルD8の値が一致します。さらに、セルB4に入力されたk,αの値が1であれば、指数分布の累積分布関数の値とも一致します。セルB3〜B5にいろいろな値を入力して確かめてみてください。
なお、参考として、サンプルファイルの[分布同士の関係 (詳細版)]ワークシートに、条件付き書式を使ってそれぞれの分布の関係を見やすくした例を含めてあります。k,αの値によって、どの値が同じになるかが視覚的に確認できます。ぜひ試してみてください。
コラム ガンマ分布が指数分布の和ってどういうこと?
「ガンマ分布は、独立した指数分布の和である」というお話が何回か登場しました。それはいったいどういうことでしょうか。これについても、数式で解き明かすのはやや難しいので、Pythonのプログラムを使ってシミュレーションしてみましょう。
サンプルプログラムはこちらから参照できます。リンクをクリックすれば、ブラウザが起動し、Google Colaboratoryの画面が表示されます(Googleアカウントでのログインが必要です)。最初のコードセルをクリックし、[Shift]+[Enter]キーを押してコードを実行してみてください。結果は図8のようになります。コードの詳細については解説しませんが、コメントとリスト1の説明を見れば何をやっているかが大体分かると思います。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon, gamma
p = 3/10 # 10分間に平均3匹の猫が通るものとする
# 2つの指数分布からランダムにサンプルを抽出
sample1 = expon.rvs(scale=p, size=10000)
sample2 = expon.rvs(scale=p, size=10000)
# 指数分布の和を求める
sample_sum = sample1 + sample2
# 指数分布の和をヒストグラムにする
plt.hist(sample_sum, bins=100, density=True)
# ガンマ分布の確率密度関数を描く
x = np.linspace(0, 6, 100) # 0〜6を100個に分けた値
gamma_pdf = gamma.pdf(x, a=2, scale=p) # α=2のガンマ分布
plt.plot(x, gamma_pdf)
plt.show()
λ=3での例(コードではλの値をpという変数に代入している)。
expon.rvs関数は指数分布からランダムにサンプルを抽出するための関数。引数scaleにはλの値を指定する。expon.rvs関数を使って抽出した10000個のサンプルを2組作り、それぞれの値の和を求めたsample_sumを基にヒストグラムを作成する。
次に、gamma.pdf関数を使ってガンマ分布の確率密度関数の値を求める。確率変数xの値は0〜6までを100個に分割した値。引数aがガンマ分布の母数αに当たる。これには、独立した指数分布の個数である2を指定する。gamma.pdf関数では、引数scaleにβの値ではなくλの値をそのまま指定する。
このようにして求められた確率密度関数の値の並びを折れ線グラフにし、確率密度関数のグラフを描く。
実行結果は以下の通りです(図8)。独立した指数分布の和がガンマ分布と一致することが分かります。
今回はガンマ分布について、指数分布との違いを見た後、具体的な利用例を基に考え方や、確率密度関数と累積分布関数の求め方などについてお話ししました。また、ポアソン分布との関係についても解説しました。ガンマ分布も指数分布と同様、広く応用できそうだということもご理解いただけたと思います。
次回は、いわゆるA/Bテスト(2つのWebサイトのデザインを作成し、どちらがより購買に結び付くかを分析するなど)やベイズ統計の事前分布としてよく使われたりするベータ分布についてお話しします。次回もお楽しみに!
この記事で取り上げた関数の形式
関数の利用例については、この記事の中で紹介している通りです。ここでは、今回取り上げた関数の基本的な機能と引数の指定方法だけを示しておきます。
ガンマ分布の確率密度関数や累積分布関数の値を求めるための関数
GAMMA.DIST関数:ガンマ分布の確率密度関数や累積分布関数の値を求める
形式
GAMMA.DIST(x, α, β, 関数形式)
引数
- x: 目的の時間(確率変数)の値を指定する。
- α: 目的の時間内に事象が何回以上起こるかを指定する。
- β: 単位時間内で事象が起こる平均の間隔を指定する。
- 関数形式: 以下の値を指定する。
- FALSE …… 確率密度関数の値を求める
- TRUE …… 累積分布関数の値を求める
「やさしい確率分布」
Copyright© Digital Advantage Corp. All Rights Reserved.


 羽山博
羽山博
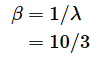
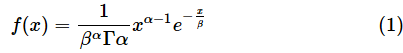

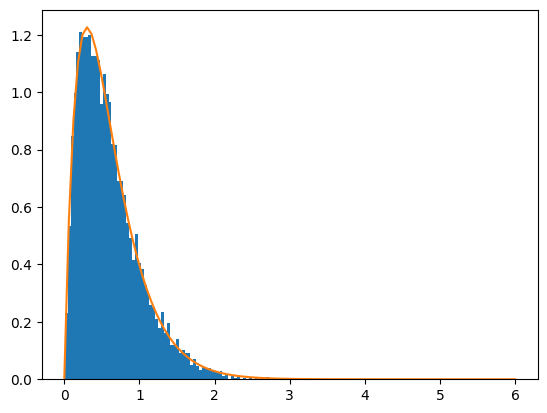 図8 指数分布の和をヒストグラムにしたものとガンマ分布の確率密度関数
図8 指数分布の和をヒストグラムにしたものとガンマ分布の確率密度関数



