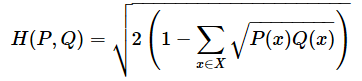ヘリンガー距離（Hellinger distance）とは？：AI・機械学習の用語辞典

2つの確率分布間の“距離”を測る指標で、値は0（一致）～1（不一致）の範囲に収まる。ユークリッド距離に似た計算式で定義されており、確率分布の違いを直感的に扱えるのが特徴である。主に統計学や機械学習の分野で、確率分布間の比較や類似度評価に利用されている。

» 2025年09月10日 05時00分公開

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

　統計学／機械学習／情報理論におけるヘリンガー距離（Hellinger distance）とは、2つの確率分布間の“距離”を測る指標である。値は0～1の範囲に収まり、0なら「完全に一致した分布（＝完全に重なっている）」、1なら「完全に不一致な分布（＝全く重ならない）」を意味する（図1）。

図1　ヘリンガー距離のイメージ

　詳しい計算方法は後述するが、平方根を含む数式定義により、数式の形は「ユークリッド距離」に近く、分布Pと分布Qの違いを直感的に理解しやすい“距離”として捉えられるのが特徴だ。

用途

　ヘリンガー距離は「確率分布同士の違い」を評価できるため、主に統計学や機械学習の分野で、次のような場面に利用される。

ベイズ推定／統計的検定： モデルの事前分布と事後分布の差、または推定分布と理論分布の差を評価する。
クラスタリング： 各クラスタを確率分布で表現し、それらの距離を測る。
生成モデルの評価： 実データ分布と生成データ分布の距離を測る。
情報検索／類似度検索： 文書の単語分布間や頻度分布間の距離を測る。

ヘリンガー距離が使われる確率分布

　KLダイバージェンスと同じ確率分布（ベルヌーイ分布、二項分布、正規分布など）に適用できる。詳しくはKLダイバージェンスの記事を参照してほしい。

定義と数式

　ヘリンガー距離を定義する数式は、確率分布の種類（離散型／連続型）によって異なる。前提条件として、

という2つの確率分布があるとする。

離散型確率分布の場合

　離散型（例えばサイコロやコイン投げなど）の場合、この2つの確率分布のヘリンガー距離は、以下のように表される。ユークリッド距離の計算に似ており、確率分布同士の「重なり具合」を距離として測れるのが特徴である。

H(P,Q) …… 「ヘリンガー距離」を指す。
Σ …… 「総和」を表す。その右側で計算した値を全て合計すること。
√ …… 「平方根」を表す。ある数を二乗したときに元の値になる数を求める計算。例えば、√4＝√2²＝2。
P(x), Q(x) …… 確率質量関数（PMF）。その関数の計算結果は、離散的なxに対する「確率」そのものを表す。

　この計算式の意味を簡単に説明しておこう。まず、離散的なxに対する確率を、分布Pと分布Qのそれぞれから計算し、得られた2つの確率値の「差」を求める。

　ヘリンガー距離では、この差をそのまま計算するのではなく、あらかじめ「確率の平方根」を取る。これは、計算結果を常に0～1の範囲に収めるための工夫であり、さらに先頭の1/√2と組み合わせることで、計算結果の最大値は1に正規化される。

　ここで話を「差」の計算に戻すと、全てのxに対して「確率の平方根」の差を二乗し、それらを全て合計（＝総和）する。最後に、その合計値に平方根を取った値を「距離」として採用する。この「差を二乗して平方根を取る」流れはユークリッド距離と同じであり、単位を元に戻す効果を持つ。

　※なお、文献によっては、ヘリンガー距離を次のように定義している場合もある。

　これは、先ほどの数式を整理して得られる等価な式表現であり、計算結果は全く同じとなる。ちなみに、この式に現れる「Σ √P(x)Q(x)」はバタッチャリヤ係数（Bhattacharyya coefficient）と呼ばれ、関連する指標としてバタッチャリヤ距離（Bhattacharyya distance）も定義されているが、本稿では詳しい説明を割愛する。

連続型確率分布の場合

　連続型（例えば身長の分布など）の場合、2つの確率分布のヘリンガー距離は、以下のように表される。

∫_－∞^∞ …… 「積分」を表す。その右側で計算した値を、指定された範囲（この例では－無限大～無限大）で連続的に合計する操作。
dx …… 積分の対象となる1つの小さな単位で、変数xでの「微小な変化量」を表す。例えば∫ f(x)dxは、「関数f(x)をxについて積分すること」を意味する。
P(x), Q(x) …… 確率密度関数（PDF）。その関数の計算結果は、連続的なxに対する「確率密度」を表す。※本来、連続型の確率分布は小文字（p(x), q(x)）で表すことが多いが、この記事では離散型との統一を重視して大文字（P(x), Q(x)）を用いている。