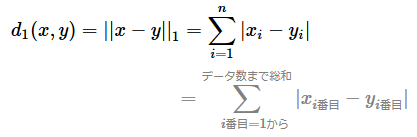マンハッタン距離（Taxicab distance）／ユークリッド距離（Euclidean distance）、L1／L2ノルムとは？：AI・機械学習の用語辞典

用語「マンハッタン距離」「ユークリッド距離」について説明。いずれも2点間の距離を計測する方法のこと。マンハッタン距離とは、碁盤の目状の道を縦に横にとタクシーが進むようにn次元の距離（＝差）の絶対値を合計することで距離を計算する方法。ユークリッド距離とは、n次元の距離（＝差）の二乗値を合計した値の平方根を求める（＝ピタゴラスの定理を適用する）ことで直線的な最短距離を計算する方法を意味する。

» 2024年09月09日 05時00分公開

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

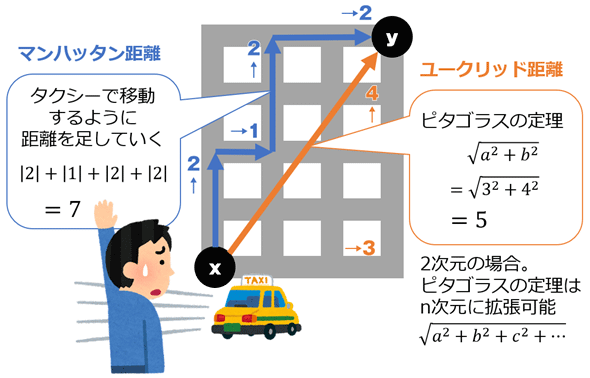
　数学／統計学／機械学習におけるマンハッタン距離（Taxicab geometry：タクシー幾何学、Taxicab metric、Manhattan distance）とは、2点間の距離を計測する際に、n次元ベクトルの次元ごとに距離（＝成分間の差）の絶対値を求めて、最後に全次元の値を合計する方法である。もっと直感的に説明すると、碁盤の目のような格子状の道を（Taxicabという名称通りに）タクシーが、例えば左下にあるx地点から右上にあるy地点に向けて、まず上に進み（＝1つ目の次元）、次に右に進む（＝2つ目の次元）、……という複数の動き（＝差）の大きさ（＝絶対値）を全部足し合わせることで、最終的な距離を計算する方法である（図1）。

図1　マンハッタン距離／ユークリッド距離のイメージ

　それに対し、ユークリッド距離（Euclidean distance、Euclidean metric）とは、2点間の距離を計測する際に、ピタゴラスの定理の公式を適用して直線的な最短距離を求める方法である。なお、ピタゴラスの定理（＝三平方の定理）とは、直角三角形をなす3辺の関係を表す、

という公式のことである。これはaとbという2次元に対する公式だが、

という3次元にするなど、多次元（n次元）に拡張してもピタゴラスの定理は成立する。よって先ほどと同様に説明すると、碁盤の目の道で例えば左下にあるx地点から右上にあるy地点に向けて、1つ目の次元、2つ目の次元、3つ目の次元、……という複数の辺（＝2点間の差）をそれぞれ二乗して全部足し合わせ、最後にその平方根を取ることで（つまりピタゴラスの定理を適用することで）、最終的な距離を計算するのが、ユークリッド距離の計算方法となる（図1）。

「マンハッタン距離」の定義と数式

　点xから点yのマンハッタン距離を求める数式は、以下のように定義できる。

　この数式では、2つのn次元ベクトルで各成分の差の絶対値を計算し、それらの合計値を「距離」として採用している。

　||……||という数学記号は、ベクトル空間における「長さ／距離」を表現する概念であるノルム（norm）を意味する。マンハッタン距離は、L₁ノルムとも呼ばれる。ちなみにL1ノルムは、NumPyライブラリのnp.linalg.norm(＜x-y点間距離の配列データ＞, ord=1)関数で計算できる。

　xを予測値ŷ、yを正解値yとするなら、この式は平均（1/n）していないだけで平均絶対誤差（MAE）やL1損失と同じ式であることに気付くだろう。つまり、MAE／L1損失は予測値と正解値の誤差（＝距離）をマンハッタン距離の手法で計算したものといえる。

「ユークリッド距離」の定義と数式

　点xから点yのユークリッド距離を求める数式は、以下のように定義できる。

　この数式では、2つのn次元ベクトルで各成分の差の二乗値を計算し、それらの合計値に対して、平方根を取った値を「距離」として採用している。

　ノルムを意味する||……||で表現した通り、ユークリッド距離は、L₂ノルムとも呼ばれる。ちなみにL2ノルムは、NumPyライブラリのnp.linalg.norm(＜x-y点間距離の配列データ＞, ord=2)関数で計算できる。

【応用】正規化ユークリッド距離と標準化ユークリッド距離

　データの特性やスケールの違いに対応するため、ユークリッド距離は正規化や標準化されることもよくある。これらについて簡単に紹介しておこう。

　正規化ユークリッド距離とは、Min-Max法による正規化（Normalization）を採用する場合、n次元ベクトルの各成分でその値の範囲が異なる場合に、次元ごとの値を最小値0～最大値1になるようにスケーリングした後に、ユークリッド距離を計算する方法である。これにより、各成分のスケールが異なるベクトル同士でも、成分間の影響を均等にして距離を比較できるようになる。

　標準化ユークリッド距離とは、一般的な標準化（Standardization、Z-score normalization）を実施する場合、n次元ベクトルの各成分でその値の範囲が異なる場合に、次元ごとの値を平均0、標準偏差1（＝分散1）になるように（＝各データポイントが標準正規分布に従うように）スケーリングした後に、ユークリッド距離を計算する方法である。これにより、各成分の平均値や分散が異なるベクトル同士でも、スケールの違いを考慮して距離を比較できるようになる。