ワッサースタイン距離（Wasserstein distance）とは？：AI・機械学習の用語辞典

2つの確率分布間の“距離”を測る指標で、「ある分布をもう一方に重ねるために、どれだけ“確率質量”を動かす必要があるか」を表す。値が0なら「完全一致」、大きいほど「異なる」ことを意味する。主に統計学や機械学習で使われ、データドリフト検出や生成モデル（WGAN）などに応用される。別名「アースムーバー距離」。

» 2025年09月19日 05時00分公開

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

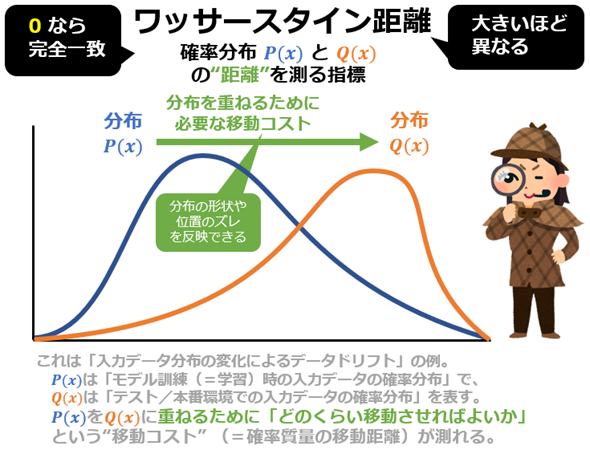
　統計学／機械学習におけるワッサースタイン距離（Wasserstein distance）とは、2つの確率分布の“距離”を測るための指標である。数理最適化の分野で研究されてきた最適輸送理論に基づいて定義されており、その特徴は「分布の形状」や「分布の位置のズレ」を自然に反映できる点にある。直感的には「ある分布をもう一方の分布に重ね合わせるために、どれだけ“確率質量”（＝分布における確率）を移動させる必要があるか」を表す（図1）。

図1　ワッサースタイン距離のイメージ

　別名として「アースムーバー距離（EMD：Earth Mover's Distance）」とも呼ばれるが、これは特に「p＝1の場合のワッサースタイン距離」（詳細後述）を指すことが多い。

　なおワッサースタイン距離の値は、常に0以上となり、0なら「完全に一致した分布（＝完全に重なっている）」を意味する。値が大きいほど「異なる」ことを示すが、その上限は分布や定義の仕方によって異なる。

用途

　ワッサースタイン距離は「確率分布同士の違い」を評価できるため、主に統計学や機械学習の分野で、次のような場面に利用される。

データドリフト／概念ドリフト検出： 学習時と運用時で入力データやラベルの分布が変化していないかどうかを監視する。
クラスタリングやデータ解析： データ群を確率分布として表現し、それらの間の「最適輸送コスト」を距離として評価する。
生成モデルの学習： 特にWasserstein GAN（WGAN）では、実データ分布と生成データ分布の距離を安定的に評価する指標として採用され、GAN研究の大きな転換点となった。
経済学・物流分野： 数理最適化の「輸送コスト最小化問題」としての数理モデルに基づいており、経済学、物流計画、都市計画など、AI以外でも応用範囲が広い。

　なお、他の距離指標（KLダイバージェンスやヘリンガー距離など）は「確率の数値的な差異」を重視するのに対し、ワッサースタイン距離は「空間上での“確率質量”の移動」を考える点が異なる。そのため、確率分布の「形状」や「位置ズレ」を直接的に捉えられる点が大きな特徴である。

ワッサースタイン距離が使われる確率分布

　ベルヌーイ分布、二項分布、正規分布など、離散型／連続型を問わず幅広い確率分布に適用可能である。主な確率分布について詳しくは、KLダイバージェンスの記事を参照してほしい。

　また、ワッサースタイン距離は「有限の距離を計算できる」点に特徴があり、KLダイバージェンスでは扱いにくい状況でも有効である。例えば「一方の分布では出目6が絶対に出ないサイコロ」と「1～6の全ての目が出るサイコロ」を比べると、KLダイバージェンスでは計算が無限大になってしまう。一方、ワッサースタイン距離は「出目6の確率を他の目に移すコスト」として扱えるため、有限の距離として計算できる。

定義と数式

　まず前提条件として、

という2つの確率分布を考える。このとき、ワッサースタイン距離の基本的な考え方は「確率分布Pから分布Qへと“確率質量”を運ぶときの最小コスト」である。これを最も一般的に表す数式は次の通りである。これを本稿では「一般形」と呼ぶことにする。

p …… 距離のスケーリングを決めるパラメーター。例えばp＝1なら「移動距離そのもの」、p＝2なら「移動距離の二乗」を基準にしてコストを計算する。pを大きくするほど、遠くへ輸送することへのペナルティ（＝コスト）が重くなるイメージになる。
W_p(P,Q) …… p次のワッサースタイン距離。ここで「p次」とは、距離の評価に「距離のp乗」を使い、最後に1/p乗してスケールを戻す形で定義されることを意味する。p＝1なら移動距離の合計、p＝2ならユークリッド距離に似た形になる。特にp＝1の場合を「アースムーバー距離」と呼ぶ。
inf（インフィマム） …… 「下限（最小値に近い値）」を取ることを表す。ここでは「全ての輸送計画の中で最小のコスト」を選ぶことを意味する。
γ（ガンマ） …… 「輸送計画」を表す記号。分布Pから分布Qへ、どのくらいの“確率質量”をどの位置に運ぶかを指定する。
Π(P,Q)（パイ） …… 分布PとQを同時に持つ“結合分布（カップリング）”の集合。つまり「PからQへ質量を運ぶ全ての方法」の候補をまとめたもの。
|x－y| …… 点xと点yの距離を表す。1次元（例えば身長の分布）なら単なる差の絶対値、多次元（例えば身長と体重の分布）なら通常はユークリッド距離になる。
|x－y|^p …… 質量を点xから点yへ運ぶときの輸送コスト。距離のp乗で評価する。
∫ dγ(x,y)（インテグラル） …… 「どのくらいの“確率質量”を、どこからどこへ運ぶか」を合計する積分。輸送計画γに従って全体を合算している。

　この式の意味を平易に言い換えると、「分布Pを分布Qに変えるためのあらゆる輸送計画を考え、その中で“輸送コスト”が最も小さいものを選び、その大きさを“距離”として採用する」ということである。ここでの“輸送コスト”とは、「距離|x－y|のp乗」と「運ぶ“確率質量”」とを掛け合わせ、全て合計した値である。

　この数式はあくまで一般形であり、実際の計算では確率分布の種類によって式の形が変わる。特に、確率分布が「離散型」の場合と「連続型」の場合で、数式を少し書き換える必要がある。

離散型確率分布の場合

　離散型（例えばサイコロやコイン投げなど）の場合、この2つの確率分布のワッサースタイン距離は、一般形の式を「総和（Σ）」の形に書き換えることで以下のように表される。

min（ミニマム） …… 「最小値を取る」という意味。ここでは「全ての輸送計画γ_ijの中で、輸送コストが最小のもの」を選ぶことを表す。
Σ_i,j（シグマ） …… 「総和記号」。iとjの全ての組み合わせ（全てのx_iとy_jの組み合わせ）に対して足し合わせることを意味する。
x_i …… 分布Pが取り得る具体的な値。例えばサイコロなら「1～6の目」、コインなら「表・裏」に対応する。
y_j …… 分布Qが取り得る具体的な値。
γ_ij（ガンマ） …… 値x_iから値y_jへ、どれだけの“確率質量”を運ぶかを表す変数（輸送計画）。
※制約条件 …… γ_ijは「輸送計画」を表すため、次の制約を満たす必要がある。
- 各x_iから送り出す総量（Σ_j γ_ij）はP(x_i)に一致する。
- 各y_jが受け取る総量（Σ_i γ_ij）はQ(y_j)に一致する。

　この数式の意味は、「分布Pの値ごとに、どのくらいの“確率質量”を分布Qの値へ運ぶか」を考え、それぞれにかかるコスト（＝距離のp乗×運ぶ量）を全て合計するということである。そして、その合計が最も小さくなるような運び方を選んだときの値が、ワッサースタイン距離となる。

　なお本稿では、数理最適化（最適輸送理論）の文脈に従い、“確率質量”という表現を、「離散型確率分布で確率質量関数（PMF：Probability Mass Function）から得られる確率」だけでなく、「連続型確率分布で確率密度関数（PDF：Probability Density Function）を区間で積分して得られる確率」に対しても、統一して用いている。ここでいう“確率質量”とは、最適輸送における「移動させる量」を指すものである。

連続型確率分布の場合

　連続型（例えば身長の分布など）の場合、2つの確率分布のワッサースタイン距離は、最初に示した一般形（積分を用いた定義式）そのものである。よって繰り返しになるため、ここではその数式の説明は省略し、特に1次元かつp＝1の場合に成立する簡単な式を示す。ここでの「1次元」とは、確率分布が1つの変数で表される場合（例：身長の分布など）を意味する。一方「2次元」とは、確率分布が2つの変数で表される場合（例：身長と体重を同時に扱う分布など）である。

F_P(x) …… 分布Pの累積分布関数（CDF：Cumulative Distribution Function）。確率密度関数を－∞からxまで積分して得られる。
F_Q(x) …… 分布Qの累積分布関数（CDF）。確率密度関数を－∞からxまで積分して得られる。
|F_P(x) － F_Q(x)| …… 2つの分布における「累積確率の差」の大きさ。
∫_－∞^∞ ⋅ dx …… その差を全てのxについて合計する操作（積分）。

　この数式の意味は、「分布Pと分布Qの累積分布関数の差」を数直線上の全てのxについて調べ、その差の大きさを積分（＝全区間で合計）するということである。直感的には、数直線上のあらゆる点で「一方の分布Pがもう一方の分布Qに対してどのくらい進んでいるか、あるいは遅れているか」を測り、そのズレを合計したものがワッサースタイン距離W₁になる。

「AI・機械学習の用語辞典」