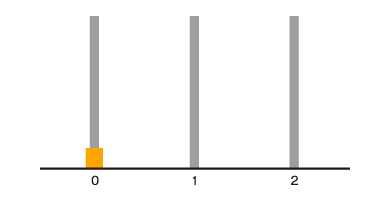再帰でハノイの塔を攻略せよ：コーディングに役立つ！アルゴリズムの基本（3）（3/3 ページ）

» 2008年10月01日 00時00分公開

[山下寛人，オイシックス株式会社]

前のページへ 1|2|3 　　　　　　

ハノイの塔を攻略せよ

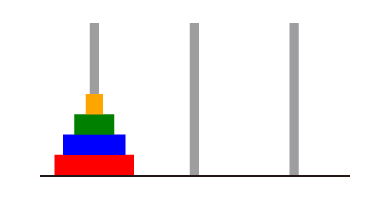
　ハノイの塔という一種のパズルがあります。

3本の棒があり、大きさの違う円盤がいくつかあります
円盤はすべて一番左の棒にささっています
最も大きい円盤が一番下に、上に行くに従って小さい円盤になっていきます
この円盤をすべて一番右の棒に移動します
ただし、一度に1つの円盤しか移動できません
小さい円盤の上に大きい円盤を置くことはできません
上に置くことができるのはその円盤より小さい円盤だけです

　このパズルをコンピュータに解かせてみましょう。

　最も単純なケースから考えてみましょう。まず円盤が1個の場合を考えます。棒に番号を付けます。左の棒を0、真ん中を1、右の棒を2とします。

　この場合は円盤を棒0から棒2に移せば終了です。

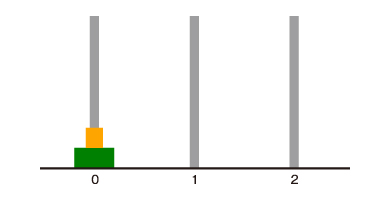
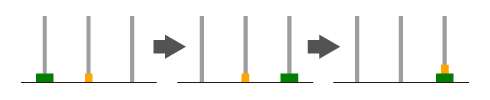
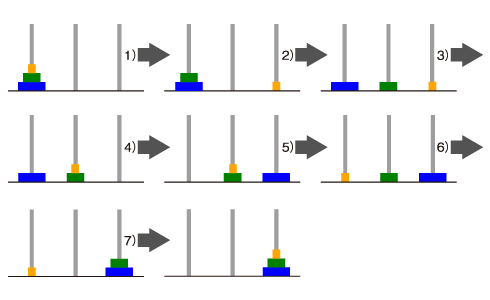
　次に円盤が2個の場合を考えます。

　まず、オレンジ色の円盤を0から1に移動し、緑の円盤を0から2に移動し、オレンジ色の円盤を1から2に移動します。ここまでは簡単です。

　では、円盤が3つの場合はどうなるでしょうか。次のような手順で解くことができます。

　説明を簡略化するためにどの棒からどの棒に移動するか、棒の番号だけで示します。

0から2
0から1
2から1
0から2
1から0
1から2
0から2

　ここで、最初の状態と手順3の後の状態に着目しましょう。最初の状態から手順3の後の状態にするには、上の2つをまとめて真ん中に移動させればよいはずです。円盤が2つの場合の移動の手順はすでに分かっているので、その手順に従って手順3の後の状態にすることができます。

　そして手順4の後の状態と最後の状態に着目します。手順4の後の状態から最後の状態にするには、真ん中の2つの円盤をまとめて右の棒に移動させればよいはずです。これも同じ要領で2つの円盤を右に移動できます。

　全部移動できたので、円盤3つをまとめて移動する手順が確立されました。

　同じ要領で円盤が何個に増えても移動させることができます。つまり以下のような手順になります。円盤の数をnとします。

左の棒からn-1個の円盤を真ん中の棒に移動させる
一番大きい円盤を左の棒から右の棒に移動させる
真ん中の円盤を全部右の棒に移動させる

　円盤が4個の場合を考えます。左から3つの円盤を真ん中に移動します。3つの場合の移動の手順は先ほど見たとおりです。左から一番大きい円盤を右に移動します。真ん中の3つの円盤をまとめて右にまとめて移動します。5個、6個と円盤を増やしていっても同じ手順で移動させられることが分かると思います。

ハノイの塔をプログラミング！

　では、これをプログラムしてみましょう。手順から分かるとおり、再帰を使うとうまくプログラムできます。少々長いですががんばってください。

<html>
<head>
<script type="text/javascript">
  function process(from, to) {
    this.moveFrom = from;
    this.moveTo = to;
  }
  var processList = new Array();
  var index = 0;
  function hanoi(from, to, spare, numberOfDisk) {
    if (numberOfDisk > 1) {
      hanoi(from, spare, to, numberOfDisk - 1);
      processList.push(new process(from, to));
      hanoi(spare, to, from, numberOfDisk - 1);
    } else {
      processList.push(new process(from, to));
    }
  }
  var disks = 4;
  hanoi(0, 2, 1, disks);
 
  function tower(id) {
    this.id = id;
    this.step = new Array();
  }
  tower.prototype.set = function(disk) {
    this.step.push(disk);
  }
  tower.prototype.get = function() {
    if (this.step.length > 0) {
      return this.step.pop();
    }
    return 0;
  }
  tower.prototype.move = function(toTower) {
    toTower.set(this.get());
  }
 
  var towers = new Array(new tower(0), new tower(1), new tower(2));
  for (i = 0; i < disks; i++) {
    towers[0].set(disks - i);
  }
  var diskId = new Array("", "one", "two", "three", "four");
 
  function move() {
    if (processList.length == 0) {
      return;
    }
    var p = processList.shift();
    towers[p.moveFrom].move(towers[p.moveTo]);
    displayTower();
  }
 
  function displayTower() {
    for (i = 0; i < 3; i++) {
      for (j = 0; j < disks; j++) {
        var diskStatus = towers[i].step[j];
        if (diskStatus > 0) {
          var disk = document.getElementById(diskId[diskStatus]);
          disk.style.top = (3 - j) * 20 + 120;
          disk.style.left = (i * 100) + 60 + (4 - diskStatus) * 10;
        }
      }
    }
  }
</script>
<style type="text/css">
.bar {
  position: absolute;
  width: 10;
  height: 150;
  background-color: gray;
}
</style>
</head>
<body onload="displayTower()">
<input type="button" value="move" onclick="move()" />
<div class="bar" style="top: 50; left: 95;"></div>
<div class="bar" style="top: 50; left: 195;"></div>
<div class="bar" style="top: 50; left: 295;"></div>
 
<div style="position: absolute;
  width: 310; height: 2;
  background-color: black;
  top: 200; left: 50"
></div>
 
<div id="four" style="position: absolute;
  width: 80; height: 20;
  background-color: red;"
></div>
 
<div id="three" style="position: absolute;
  width: 60; height: 20;
  background-color: blue;"
></div>
 
<div id="two" style="position: absolute;
  width: 40; height: 20;
  background-color: green;"
></div>
 
<div id="one" style="position: absolute;
  width: 20; height: 20;
  background-color: orange;"
></div>
 
</body>
</html>

　htmlファイルをWebブラウザで開くと塔が表示されます。左上の「move」ボタンをクリックすると1つずつ円盤が移動していきます。

4～20行目

最初に手順をすべて計算します。processオブジェクトは1回の移動でどの棒からどの棒へ移動させるかを表します。どの円盤を移動させるかは、必ず移動元の棒の一番上の円盤になるので、手順の情報には必要ありません。processListはprocessのリストです。手順の順番に配列に格納します。

10～18行目

先ほど解説したアルゴリズムのとおりハノイの塔を解く関数を実装しています。円盤が1つの場合は単純にfromからtoへ移動します。

19行目

円盤の数を指定しています。

20行目

関数を呼び出し、手順をすべて計算します。

22～37行目

ここから先はすべて表示のためのプログラムです。1つの棒を表すtowerクラスを定義しています。

22～25行目

towerクラス本体です。idは左の棒（0）、真ん中の棒（1）、右の棒（2）を表す変数。stepは、棒の一番下がstep[0]、その上がstep[1]、その上がstep[2]、以降その繰り返しです。step[n]の値は円盤の状態です。0の場合は何もなし、1以上の場合はその数値の大きさの円盤があります。

26～28行目

棒に円盤を追加するメソッドです。配列stepの末尾＝一番上にdiskを追加します。

29～34行目

棒から円盤を取るメソッドです。stepのlengthが0の場合は円盤がありませんので、0より大きい場合に一番上の円盤の数値を取得して返します。pop()は配列の末尾の値を取得して、配列から削除します。ちなみにこのデータ構造もスタックになっています。

35～37行目

toTowerの棒に、円盤を移動するメソッドです。

39行目

3つの棒を生成しています。

40～42行目

左の棒に円盤を4つセットしています。棒と円盤の状態を図にすると次のようになります。


towers[0].step[3]＝1	towers[1].step[3]	towers[2].step[3]
towers[0].step[2]＝2	towers[1].step[2]	towers[2].step[2]
towers[0].step[1]＝3	towers[1].step[1]	towers[2].step[1]
towers[0].step[0]＝4	towers[1].step[0]	towers[2].step[0]

43行目

円盤の、HTML上のIDを定義しています。後でdocument.getElementById()を実行するためのものです。

45～52行目

1回の移動を行う関数です。

46～48行目

processListに何も残っていない場合はそのまま関数の実行を終了します。

49行目

現在の手順を取得します。shift()は配列の先頭の値を取得し、配列から削除します。従ってshift()を繰り返すと順番に手順を取得でき、最後にはすべて削除され何もなくなります。

50行目

手順に従い棒から棒へ円盤を移動します。

51行目

現在の円盤の状態を表示します。

54～65行目

現在の状態に従って円盤を表示します。

67～74行目

棒の形をスタイルシートのクラスとして定義しています。3本の棒は同じ形なのでクラスとして定義すると無駄がありません。

76行目

bodyのonloadイベントで円盤の初期状態を表示するようにしています。onloadはWebブラウザがHTMLをすべて読み込んだ後のタイミングで実行されます。

78～80行目

3本の棒を表示しています。

82～86行目

3本の棒の下の土台のような線です。

88～106行目

表示する円盤を定義しています。位置はdisplayTower関数で計算するのでここでは指定していません。

　移動する様子を表示する部分がやや長くてややこしいですが、パズルを解くhanoi関数は非常に短くスマートです。

　再帰を使ったプログラムは必ず再帰を使わないで書くことができます。ハノイの塔も同様です。興味があれば考えてみるとよいでしょう。

　また、hanoi関数自体は円盤の数がいくつに増えても対応できます。円盤を表示する部分が4個までしか対応していませんが、表示させる部分もいくつに増えても大丈夫なように拡張してみるのもよいかもしれません。

　ここまで見てきたように再帰を使うと分かりやすくスマートにプログラムを書ける場合があります。次回以降たびたび出てきますのでぜひ覚えておいてください。次回はさまざまなソートのアルゴリズムを解説します。

著者紹介

山下寛人

オイシックス株式会社

「次回」へ

「コーディングに役立つ！アルゴリズムの基本」バックナンバー

いまさらアルゴリズムを学ぶ意味
コーディングに役立つ！アルゴリズムの基本（1）　コンピュータに「3の倍数と3の付く数字」を判断させるにはどうしたらいいか。発想力を鍛えよう
Zope 3の魅力に迫る
Zope 3とは何ぞや？（1）　Pythonで書かれたWebアプリケーションフレームワーク「Zope 3」。ほかのソフトウェアとは一体何が違っているのか？
貧弱環境プログラミングのススメ
柴田淳のコーディング天国　高性能なIT機器に囲まれた環境でコンピュータの動作原理に触れることは可能だろうか。貧弱なPC上にビットマップの直線をどうやって引く？
Haskellプログラミングの楽しみ方
のんびりHaskell（1）　関数型言語に分類されるHaskell。C言語などの手続き型言語とまったく異なるプログラミングの世界に踏み出してみよう
ちょっと変わったLisp入門
Gaucheでメタプログラミング（1）　Lispの一種であるScheme。いくつかある処理系の中でも気軽にスクリプトを書けるGaucheでLispの世界を体験してみよう