Cの型変換と式:目指せ! Cプログラマ(5)(1/2 ページ)
Cの演算子では演算対象の数値などを明示的、あるいは非明示的に変換することがあります。この仕組みをキチンと理解していないと思った通りの計算結果が出ないことも。今回は、この仕組みを徹底解説します。
前回は、いくつかの演算子と、演算子の優先順位について学びました。演算子を組み合わせて使うことで、さまざまな演算を行ったり、変数の値を変えたりすることができます。
演算子の中には、演算のときにオペランドの型を変換するものがあります。この型の変換の仕組みを知っておくことで、思い通りの計算ができるようになります。逆に、この仕組みを理解していないと、思った通りの計算結果がでずに、悩むことになります。今回は、前半で型変換について学んだあと、後半では演算子とオペランドの組み合わせである式について学びましょう。
型変換
Cでは1つの型ですべての値を表すことができません。整数を表す型だけでも、char、short int、int、long intなどがあり、さらにそれぞれについて符号なし型など、たくさんの型があります。そのため、異なる型同士での演算は頻繁に起こります。
また、同じ型同士の演算でも、その結果が元々の型に収まるとは限りません。そのようなときには型の変換が必要になってきます。
型の変換には、プログラマが変換結果の型を指定する明示的な型変換と、プログラマが指定しなくても勝手に行われる暗黙の型変換の2つがあります。
明示的な型変換のことをキャストと呼びます。キャストを行うにはキャスト演算子を使って、「(新しい型)オペランド」のように書きます。例えば、変数aをint型にキャストするためのコードは「(int)a」となります。
型の変換が行われると、それが明示的か暗黙かにかかわらず、値が変わる可能性が出てきます。変換は、できるかぎり値が変わらないように行われます。しかし、新しい型がその値を表現できない場合には、新しい型で表現できる値に変わるようになっています。
新しい型がその値を表現できず値が変わってしまうときには、次のようなルールで変換されます。
1. 整数型から整数型への変換(_Boolは除く)
ある整数型から別の整数型へ変換するときに値が変わるということは、古い型と比べて新しい型の表現可能な範囲の方が狭いときに起こります。
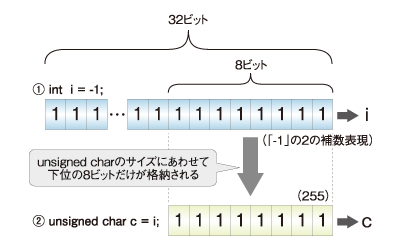
変換後の新しい型が「符号なし整数型」の場合は、その値の2の補数表現において、新しい型が表現可能なビット数分の下位ビットのみが抜き出され、上位のビットは切り捨てられます(下図参照)。
例えば、この連載で使っているPleiades(unsigned char型が8ビット、int型が32ビットの幅を持つ)の環境において、int型の-1という値を、負の値を表現できないunsigned char型に変換しようとすると、-1の2の補数表現(16進数でFFFFFFFF)の下位8ビットが抜き出され、結果は16進数のFF(10進数の255)になります。
int i = -1;
unsigned char c = i;
printf("c : %u\n", c);
c : 255
変換後の新しい型が「符号付き整数型」の場合は、コンパイラによって結果が異なります。このような変換は避けた方が無難でしょう。どうしても使う必要があるときは、コンパイラの仕様を確認して下さい。
コラム●2の補数
負の数を表すために「2の補数」というものがよく使われます。計算方法はとても単純で、「正の数を表すビットを反転させて1を加算」するだけです。8ビットで整数を表す場合にどうなるか見てみましょう。10進数の「1」は2進数では「00000001」です。これをビット反転させた「11111110」へ1を加算した結果である「11111111」が10進数の「-1」となります。負の数をこのように表現すると決めておくと、計算上いろいろと都合が良いので、約束事として覚えておきましょう。
2. 実浮動小数点型と整数型の変換(_Boolは除く)
実浮動小数点型から整数型への変換では、実浮動小数点数の整数部だけが抜き出され、小数部は切り捨てられます。ただし、切り捨てた後の値も整数型で表現できないときには、コンパイラによって処理方法が異なります。
整数部分だけ比較しても、doubleのすべての値をintで表現することはできません。doubleからintへ安全に変換するためには、その前にdouble型の値がint型で表現可能であることを確認するなどの対応をして下さい。
整数型から実浮動小数点型へ変換するときにも、値がそのまま表現できる場合にはそのままの値で変換されますが、表現できないときにはコンパイラによって処理方法が異なります。また、元の整数型の値が新しい実浮動小数点型で表現可能な範囲を超えているときは、このような変換をしてはいけません。
3. 実浮動小数点型から実浮動小数点型への変換
実浮動小数点型同士の変換では、新しい型で表現可能な上限と下限の間の値であっても、精度の問題で表現できないことがあります。変換される値は、新しい型で表現可能な範囲を超えてはいけません。
表現可能な範囲の値であれば、新しい型で表現可能な値の中で、なるべく近い値に変換されます。元の値に近い値として、もっとも近い大きな値と、もっとも近い小さな値が候補になる場合がありますが、どちらが採用されるかはコンパイラごとに決まります(*1)。
(*1)奇妙にも思える浮動小数点型のこれらの振る舞いについては、浮動小数点型の内部表現について調べると理解できるようになります。詳細な話になりますのでここでは説明しませんが、浮動小数点数の扱いは他のプログラミング言語でも似ていますので、どこかの機会でまとめて勉強すると良いでしょう。(言語はJavaとなりますが、こちらの記事も参考にどうぞ)。
暗黙の型変換
Pleiadesの環境では、unsigned char型は0から255の値だけが表現可能ですので、256や-1といった値を格納することはできません。
では、代入演算子を使ってこれらの値を、明示的な型変換を行わずにunsigned char型の変数へ代入しようとすると、どうなるのでしょうか。次のプログラムを見て下さい。
#include <stdio.h>
#include <stdlib.h>
int main(void) {
unsigned char c_one = 256;
printf("c_one(256) : %d\n", c_one);
unsigned char c_two = -1;
printf("c_two(-1) : %d\n", c_two);
return EXIT_SUCCESS;
}
c_one(256) : 0 c_two(-1) : 255
結果は、c_oneが0、c_twoが255になります。
5行目の256という定数はint型で、格納される変数の型であるunsigned charに変換されてからc_oneに入れられます。このように、元の値(この場合はint型の値)が、新しい型(この場合はunsigned char)で表現できない場合には、特定のケースにおいて自動的に型の変換が行われます。これが「暗黙の型変換」です。
このような、切り捨てによって値の変更をともなう変換以外にも、暗黙の型変換が行われるケースには次のようなものがあります。
(1) 通常の算術型変換
2つのオペランドをとるほとんどの算術型の演算子(+ - * / % など)は、演算を行う前にオペランドの型を同じ型に合わせるような変換が行われます。このような変換を「通常の算術型変換」と呼びます。
通常の算術型変換は、次の3つのステップで行われます(*2)。
- 一方が実浮動小数点型ならば、表現範囲がより広い型に合わせられます
- そうではなく両方が整数型ならば、まず整数拡張(後述)が行われます
- 整数拡張された後の型において、表現範囲がより広い型に合わせられます
(*2)ほとんどのケースではこの理解で問題ありませんが、規格ではより詳細な規定があります。
(2) 整数拡張(汎整数拡張、格上げ)
int型よりも狭い表現範囲を持つ整数型、例えばcharやshortなどは、int型、あるいはint型で収まらない場合はunsigned int型に変換されてから計算されます。
同じように、_Bool型、int型、signed int型、unsigned int型のビットフィールド(*3)についても、同じようにint型かunsigned int型に変換されてから計算されます。
(*3)ビットフィールドについては今後の連載で説明する予定です。
(3) 論理型(_Bool)
整数型および浮動小数点型とポインタ型(*4)を論理型に変換するときは、その値が0ならば0、それ以外ならば1になります。
暗黙の型変換の例を示しますので、確認してみて下さい。
- 例1)「unsigned char a」「unsigned char b」のとき「a + b」: aとbの両方が整数拡張されint型になり、和が計算されます。
- 例2)「unsigned char a」「long b」のとき「a + b」 : aが整数拡張されint型になりますが、さらにbの方が表現範囲が広いためlong型に変換され、和が計算されます。
- 例3)「double a」「char b」のとき「a + b」 : bがdouble型に変換され、和が計算されます。
(*4)ポインタ型については今後の連載で説明する予定です。
コラム●なぜ整数拡張が行われるのか
例1は、もし「a + b」の計算結果がunsigned char型に収まらなかったとしても、正しく計算が行われるということを示しています。aとbが200だったとすると、計算結果の400という数値は、8ビットの表現範囲を持つ環境のunsigned charでは収まりません。しかし整数拡張が行われることによってint型を持つため、正しく400という数値が計算されます。
注意しておきたいのは、その結果をunsigned char型の変数に代入しようとすると、そのときに上位ビットの切り捨てが行われてしまうということです。「unsigned char x; x = a + b;」としてしまうと、xでは400が表現できないため、上位ビットが切り捨てられて値が変わってしまいます。
また、整数拡張によって変換が行われるのはintとunsigned intまでです。それより大きな型(long intやlong long intなど)については拡張されません。そのため正しい計算結果を求めるために、計算結果がint型に収まらない可能性がある場合については、計算に先立って元の型をlong intやlong long intなどに変換しておくといったことが必要になります。
このように、計算結果が元の型に収まらない可能性についても、プログラマはきちんと把握しておく必要があります。
Copyright © ITmedia, Inc. All Rights Reserved.