第2回　DES暗号化：マスターIT／暗号技術

今回は長らく暗号化技術の標準規格として利用されていたDESについて解説する。DESはすでに利用は非推奨となっているが、DESの制定を契機にさまざまな暗号技術や解読技術が進化するなど、その存在意義は大きい。

» 2015年05月21日 05時00分公開

[打越浩幸，デジタルアドバンテージ]

連載目次

このマスターIT連載は、IT Pro初心者に向けて、さまざまなITテクノロジを紹介、解説するコーナーである。まずは暗号化について取り上げる。

　前回は暗号化技術の基礎について見てきた。今回は代表的な共通鍵暗号方式であるDESについて取り上げる。

　DESは安全性に対する懸念から、すでに現在では非推奨の暗号化アルゴリズムとなっている。しかし、標準規格化された暗号化アルゴリズムであることから広く普及し、その後の暗号化アルゴリズムの研究・開発などにも大きく貢献した。そのため、最新の暗号化アルゴリズムを知る上でもDESを理解しておくべきだ。

DESとは

　「DES（Data Encryption Standard）」は、1977年に米国商務省標準局（NBS：National Bureau of Standard。現NIST：National Institute of Standards and Technology）によって制定された、標準のデータ暗号化規格である。

　これは、コンピューターのデータや通信の内容を保護するために公募によって募集された共通鍵暗号方式の暗号化アルゴリズムの一つで、米IBMによって開発・提案され、最終的に標準規格として採用された。IBMが開発したLucifer（Wikipediaの解説ページ）という暗号化アルゴリズムをベースとしている。

　DESでは、64bit単位のデータに対して、ビット位置の変更（転置）やテーブル参照による置き換え（置換）、XOR演算、シフト、繰り返し処理などを組み合わせて、入力されたデータを可能な限り「かき混ぜる」という処理を行っている。実用的な暗号／復号化処理速度を実現するために、主にハードウエアでの実装を考慮して設計されている。

　DESのアルゴリズムの中には、テーブルを参照してデータの置換を行うSボックス（後述）という機能がある。当初はこのテーブルデータの並びに、開発者しか知らないバックドアが仕掛けられているのではないか（＝バックドアを使って簡単に復号できるようになっているのではないか）などの疑義が持たれ、暗号研究者によるさまざまな調査・研究が行われた。規格制定後もDESの安全性や解読方法の研究が行われるなど、その後の暗号化技術の発展にも大きく寄与したといえる。

DESによる暗号化アルゴリズム

　DESは64bit（8bytes）単位でデータを暗号化するブロック暗号アルゴリズムである。入力や鍵データが64bitに満たない場合は、ゼロデータなどを追加して64bitにそろえてから処理を行う。

　入力としては、64bitの元データと64bitの暗号化用の鍵を受け付け、暗号化処理を行って、64bitの暗号化済みデータを出力する。ただし鍵データには8bit（1byte）ごとに1bitのパリティビット情報が含まれているので、実際には56bitだけが使われる。

　DESにおける暗号化処理を図にすると次のようになる。

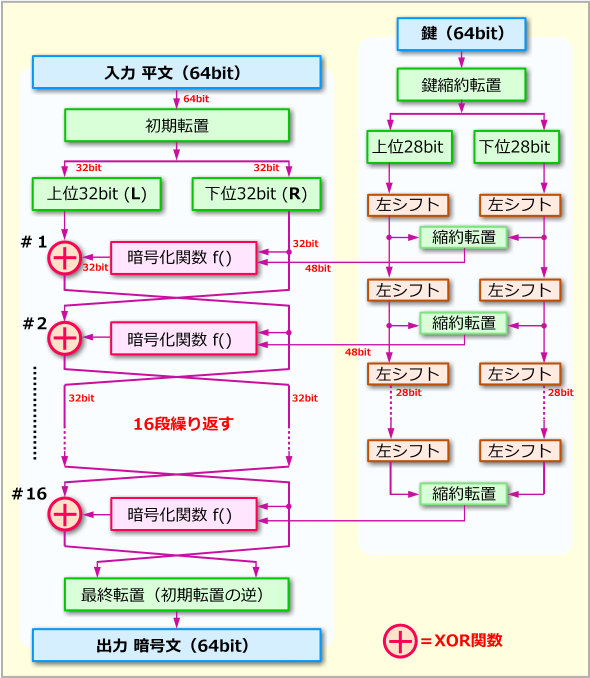DESのメインの処理
入力されたデータは32bitずつに分ける。そして上位側（L）は暗号化関数の出力とXOR演算し、上下を入れ替えて次段へ回す。16回段分の処理が終わると、それが出力となる。鍵データも半分ずつに分け、シフトと縮約転置を行って暗号化関数にサブキーとして供給する、という処理を16段分繰り返す。転置とはビット位置の入れ替え処理、縮約転置とはビットデータの抜き出し処理のこと。

　繰り返しの各段で使われる暗号化関数f()は次のようになる。

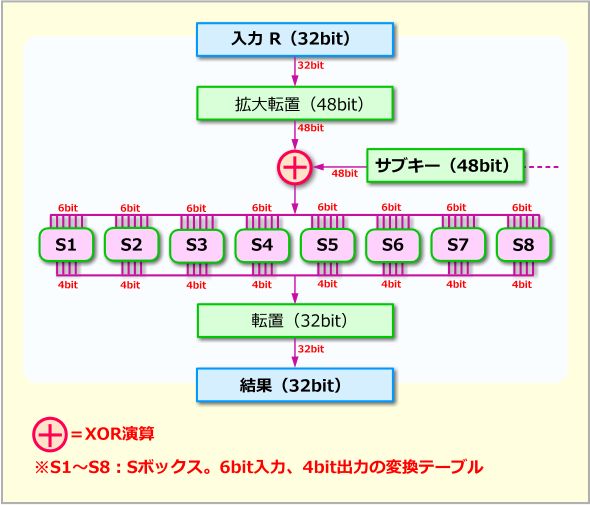DESの暗号化関数f()
入力された32bitのデータは、48bitに拡大転置後、48bitの鍵データとXOR演算し、それを6bit×8グループに分けてから、それぞれSボックスで変換する（テーブルからルックアップする）。変換後のデータは4bitずつになるので、それを8グループ分集めて、この段の出力とする。

　DESのこのような暗号化アルゴリズムは、DESの開発者Horst Feistelにちなんで「ファイステル構造（Feistel structure）」と呼ばれている。

　この方法では、入力されたデータを2つ（もしくはそれ以上）に分け、一方に「暗号化関数」による処理を適用してビットデータに何らかの変換措置を施す。そしてデータの左右を入れ替えて同じ処理を繰り返す。

　ブロック全体を一度に処理しないので、1段ごとに必要な暗号化の処理（回路の規模）が簡単になる。ただし、十分な“攪拌（かくはん）”効果を得るために、何度か繰り返すようになっている。DESの場合は、16回繰り返している。

　DESの処理をまとめると次のようになる。

1．入力された64bitのデータに対して「初期転置」を行う
2．データを上位32bit（L)と下位32bit（R）に分ける
3．以下の処理を16回繰り返す
　　a．下位32bitのデータ（R）を48bitに「拡大転置」する（32bitから6bitずつ取り出して8つのグループを作る。一部のbitは重複して利用されることになる）
　　b．鍵から48bitのデータを生成する
　　c．a．とb．をXOR演算する
　　d．c．のデータを6bitずつ8グループに分け、各グループを「Sボックス」で6bit→4bit変換する
　　e．d．の結果の32bit（4bit×8グループ）を転置してから、上位32bitのデータ（L）とXOR演算する
　　f．下位32bit（R）を次段の上位32bit（L）とし、e．の出力を次段の下位32bit（R）とする
　　g．a．へ戻り、16回繰り返す
4．3．の結果の上位と下位の32bitを合成して64bitとし、最後に「最終転置（IP-1）」を行う（最終転置は初期転置のちょうど逆変換になっている）

　「転置」とは、入力されたビット位置を別の場所へ移動させる（入れ替える）処理である。例えば「初期転置」では、第1bitを第40bitの位置へ、第2bitを第8bitの位置へそれぞれ移動させる、といった処理を行う。

　単純な加減乗除や論理演算だけでは位置に偏りができるので、暗号アルゴリズムではビット位置を大きく“攪拌（かくはん）”させるために、転置処理やシフト処理などを行っている。これにより、bitの配置がランダムになり、元のデータや鍵などを推測しにくくなる。

　「Sボックス」は、bitデータの「変換」を行う機能を持つ。DESの場合は、6bitの入力から4bitを取り出すSボックスが8つ定義されており、それぞれ異なるパターンでデータを変更している。例えば「S1ボックス」は次のように定義されている。

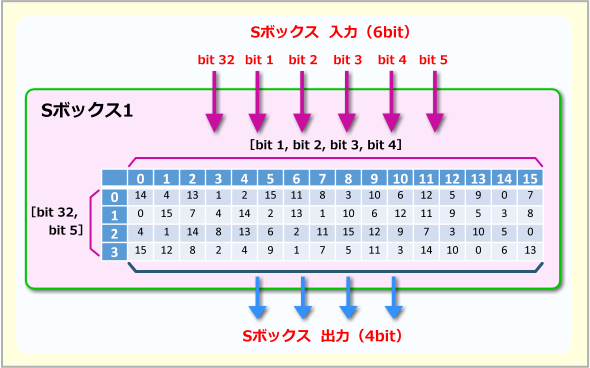Sボックスの例
これは「S1ボックス」の例。S1ボックスには、暗号化関数への入力32bitのデータのうち、「bit 32」「bit 1」「bit 2」「bit 3」「bit 4」「bit 5」の6bit分のデータが入力されている。Sボックス内では、入力された6bitのうち、両側の2bitでこの表の行を選択し、真ん中の4bitで表の列を選択する。例えば入力された6bitのデータが「110010」なら、「2（2進数では10）」の行と「9（2進数なら1001）」の列を選択して、その交点にあるデータ「12（2進数なら1100）」を出力とする。

　Sボックスは線形変換＊1ではない変換として定義されている。このため、出力から逆関数（逆変換）を使って元のデータを簡単には計算できないようになっている。

＊1 線形変換は、数学的な特性を表す用語。暗号アルゴリズムの場合は、単純な四則演算やシフトだけでは実現できないような処理を非線形という。このような演算は逆関数を定義するのが困難であり、これを使うことにより、例えば逆関数や連立方程式を使って元データと暗号データから鍵の値を得るといったことが困難になる。また、例えば入力データが0や1ばかりなど、特別なパターンの場合には鍵の値がそのまま、もしくは推測しやすい形で出力に現れる可能性がある。これを避け、さらにデータを攪拌するために、転置やSボックスによる変換処理を行う。

　またSボックスの入力を1bitだけ変えると、出力は2bit以上変わるようになっているし、1と0がなるべくランダムに出力に現れるようにも設計されている。

　Sボックスでの変換が終わると、それらを集めて32bitのデータにしてからもう1度転置し（これがラウンド関数の出力となる）、それを上位32bitのデータとXOR演算する。最後に上位32bitと下位32bitを入れ替えて、次の段の処理を始める。

　DESではこれらの処理を16回繰り返して、結果を十分攪拌するようにしている。例えば入力が1bitだけ異なるデータであっても、8段もあれば統計的に入力との相関関係がなくなることが分かっている。

　DESの暗号化処理は以上の通りである。一方、暗号化されたデータを元に戻す（復号する）には、各段の処理を逆順に適用する。もしくは、初期転置と最終転置は逆変換になっているという関係を利用して、鍵シーケンス（生成されたサブキーの列）を逆順に適用して暗号化処理を行っても復号できる。

DESの実装

　DESのアルゴリズムを図にすると、かなり複雑な処理を行っているように見える。だが実際には、ハードウエアとして実装するなら簡単なビット演算（XOR演算）とシフト、テーブル参照などだけで処理できるため、非常に高速に処理できる。

　ソフトウエアで処理する場合も、ビット演算やシフト演算などを使えば簡単に実装できる。実装例は、例えばGitHubで「DES」を検索すると多数見つかる。初期転置やSボックス、拡大転置のテーブルなどについては、これらのコードを参照していただきたい。DES処理のほとんどは、シフトやAND、XOR演算、配列参照だけでできていることが分かるだろう。

GitHubに登録されている「DES」プログラムの検索結果（GitHub）
DESのCプログラムの例（Sebastien Rannou氏のGitHubページ）

DESの暗号強度

　DESでは64bitのデータブロックと56bitのキーを使っている。だが、規格制定当初からこの程度の安全性では（将来のコンピューターの進歩などを考えると）不十分ではないかとも言われていた。

　その後、その懸念は現実のものとなり、現在では総当たり攻撃でも容易に解読できてしまうようになってしまった。そのためDESは標準規格としては非推奨となり、現在では後継のAESなどの暗号化技術の使用が推奨されている。

　DESに対する攻撃（暗号の解読）方法はいくつかある。主なものは次の通りである。

●総当たり攻撃

　可能な暗号鍵のを全て順番に試すという力ずくの攻撃方法である。DESでは56bitの鍵を採用しているため、最悪でも2の56乗通りの鍵を試行してみれば暗号を解読できることになる。

　例えば1秒に10億回（2の30乗回）の暗号化処理ができる暗号化装置、もしくはコンピューターを100万台（2の20乗台）用意すれば（最先端のスーパーコンピューターなら、1システムで100万コア以上備えている）、1秒間に1000兆回（2の50乗回）試行できるので、64秒で全数探索できてしまう。

　ちなみにDESでは、元の平文と暗号鍵を全ビット反転させると（1の補数を取ると）、結果の暗号文も全て反転したビット列になるという性質がある。そのため、正確には2の56乗回ではなく、2の55乗回の試行でよいことになる。

●差分解読法

　これは、十分な数の「選択平文（ある平文と、その結果の暗号文の組）」が入手できると仮定した場合に利用できる解読方法である。入力の一部のビットデータが変わった場合に、出力（暗号文）のどこに影響が現れるかを調べ、鍵の候補を絞り込む。

　DESでは、入力されたあるビットデータがSボックスで置換され、別の場所へ「伝播」する。その傾向を元にして、どのビット位置にどの程度の影響が出るか（確率）を計算し、鍵を推定する。この差分解読に対する耐性を高くするようにDESは設計されているものの、2の47乗個の選択平文があれば、2の47乗の手間で解読できるとされている。