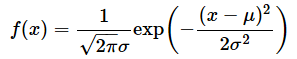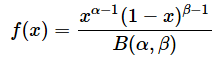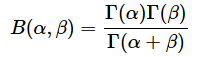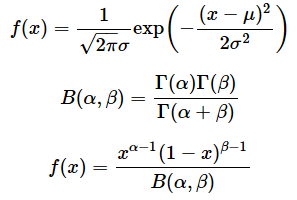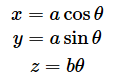Matplotlibで折れ線グラフ（正規分布など）を描こう：数学×Pythonプログラミング入門（2/3 ページ）

[羽山博，著]

目標2： 任意の関数のグラフを任意の刻み幅で描く（関数を引数として渡す）

　最初の目標であるシグモイド関数のグラフについてはクリアできました。しかし、それだけでなく、他の関数もグラフ化できれば便利です。加えて、定義域や刻み幅（増分値）も関数に合わせて自由に変えられるとうれしいですね。そこで、以下のような形式で定義されている関数を基に、xとyのリストを作ることを考えます。xとyのリストさえ用意できれば、グラフ化は容易です。

　つまり、1つのxに対して、1つのyが決まり（そもそも、数学の「関数」とはそういうものですが）、定義域がxmin〜xmax（未満）であるもの、ということです。取りあえず、関数の係数や定数項には決まった値が指定されているものとします。

　例えば、平均がμ、標準偏差がσの正規分布の確率密度関数は以下のように定義されます。

　また、ベイズ統計の事前分布などによく使われるベータ分布の確率密度関数は以下のように定義されます*4。

　分母はベータ関数と呼ばれる関数で、以下のように定義されます。

　Γ（ガンマ）はこの連載の第2回の練習問題で紹介したガンマ関数です。

*4　正規分布の確率密度関数やベータ分布の確率密度関数については、こちらで詳しく説明しています。

　今のところは、正規分布のμやσ、ベータ分布のαやβには決まった値を与えることとして、関数makedataを定義し直します。関数makedataを以下のように呼び出すことにより、どちらのグラフも描画できるようにしてみましょう。なお、関数normdist／betadist／makedataをまだ作成していないので、リスト9のコードはこの段階では実行できません。というわけで、今はそれらの関数をどのように呼び出すのかを確認しておくだけで構いません（もちろん、取りあえず入力しておいても構いません）。後で実行するときに再掲します。

import matplotlib.pyplot as plt

x, y = makedata(normdist, 0, 100, 1) # 定義域は0〜100、刻み幅は1
plt.plot(x, y)
plt.show() # 正規分布のグラフを表示

x, y = makedata(betadist, 0, 1, 0.01) # 定義域は0〜1、刻み幅は0.01
plt.plot(x, y)
plt.show() # ベータ分布のグラフを表示

リスト9　正規分布のグラフとベータ分布のグラフを描画するためのコード
関数makedataの最初の引数に、グラフ化するデータを計算するための関数の名前を指定していることに注目。
normdistは正規分布の確率密度関数の名前。ただし、μ＝50, σ＝10という値は関数normdistの中で指定するものとする。
betadistはベータ関数の確率密度関数の名前。やはり、α＝2, β＝5という値は関数betadistの中で指定する。

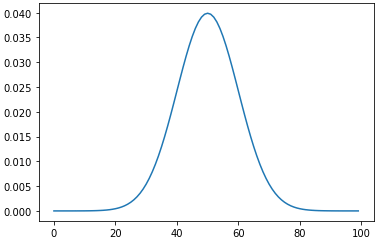
　後述のリスト11で関数normdist／betadist／makedataを作成し、リスト9を実行したときの結果は図5の通りです。これについても、腕に覚えのある方はノーヒントで関数makedata、normdist、betadistを作成し、以下のグラフが表示されるようにしてみましょう。

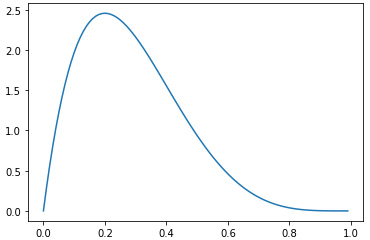図5　正規分布のグラフとベータ分布のグラフ
リスト9と後述のリスト10／リスト11により、正規分布の確率密度関数のグラフとベータ分布の確率密度関数のグラフが作成できる。関数を可視化すれば、分布のイメージや特徴などがよく分かる。

3. 任意の関数のグラフを任意の刻み幅で描く（プログラムの作成）

　いきなり難しくなったように思えるかもしれませんが、関数makedataの引数が1つ増えただけです。つまり、関数makedataの中から、normdistやbetadistなどの、指定された関数を呼び出せるようにすればいいだけです。というわけで、これに関しては数学の出番はありません。Pythonの文法を知っていれば、リスト3を少し書き換えるだけで簡単にできます。

　ですが、先を急がず、これまでと同様、

• ステップ1： 関数normdistと関数betadistを定義する
• ステップ2： xとyの値を用意する：xの値を増分値ずつ増やしながら、対応するyの値を求める
• ステップ3： plot関数にxとyを指定する

という手順通りに進めましょう。

ステップ1： 関数normdistと関数betadistを定義する

　正規分布の確率密度関数とベータ分布の確率密度関数は数式通りに定義するだけです。ここは数式をPythonのコードとして表す練習（おさらい）をかねて、穴埋め問題にしておきます（リスト10）。かっこの対応や演算子の優先順位に注意しながら1つずつ丁寧に入力していきましょう。

import numpy as np
from math import gamma

def normdist(x):
  mu = 50  # 平均
  sigma = 10  # 標準偏差
  return 1 / (np.sqrt(2*np.pi) * sigma) * np.exp(-(___ア___)**2 / (2*___イ___))

def beta(a, b): # ベータ関数の定義
  return gamma(a)*gamma(b) / (gamma(a+b))

def betadist(x):
  a = 2  # αの値
  b = 5  # βの値
  return x**(___ウ___) * ___エ___ / beta(a, b)

リスト10　正規分布の確率密度関数の定義とベータ分布の確率密度関数の定義
sqrt関数、exp関数、円周率を表す定数piはnumpyモジュールに含まれるが、gamma関数はnumpyモジュールに含まれないので、mathモジュールの関数を使う。

　定義を忘れた人のために、数式を再掲しておきます。

　答えは以下の通りです。オレンジ色の部分をクリックすると答えが表示されます。

（答え）
　　ア. 　x-mu　
　　イ. 　sigma**2　
　　ウ. 　a-1　
　　エ. 　(1-x)**(b-1)　

ステップ2： xとyの値を用意する：xの値を増分値ずつ増やしながら、対応するyの値を求める

　次の手順は、xとyの値を用意するための関数makedataの修正です。Pythonの関数では、引数に関数名を指定して関数の参照を渡すこともできるので、その記述を追加します。コードを少し書き換えましょう。仮引数として、新たに関数の参照を表すfuncを追加し、これまでのxの最小値、xの最大値、増分値と合わせて4つを指定します。

def makedata(func, xmin, xmax, step): # 関数の参照funcを受け取る
  x = np.arange(xmin, xmax, step)
  y = func(x)  # funcで参照される関数を呼び出す
  return x, y

リスト11　任意の関数のグラフを描画するためのデータを作成する
シグモイド関数のデータを作るリスト3の例と異なっているのは、仮引数としてfuncを追加したこと、yの値を作成するための関数はfuncを使って呼び出すということの2点。

　プログラミングにあまり慣れていない方とっては、関数の参照を引数として渡すというのがピンとこないかもしれません。何らかの値を関数に与えて計算する、というのは比較的スンナリと理解できると思いますが、関数に（他の）関数の参照を与えるというのはどういうことでしょうか。

　これは、パン作りなどの例え話にすると分かりやすいです。例えば、小麦粉やバターなどの材料はデータに当たります。パンをこねる作業は自分でもできますが、ホームベーカリーを使ってもできますし、力持ちの誰かに頼むこともできます。ホームベーカリーやパンをこねる人が関数に当たります。パンをこねるときに「そこにある小麦粉を使ってね」と言うのはデータを与えていることになります。一方、「そこにあるホームベーカリーを使ってね」とか「そこにいるパンこね名人に頼んでね」と言うのは関数の参照を与えることに当たります。「参照」というのは「そこにあるよ」という情報だと考えると分かりやすいですね。

ステップ3： plot関数にxとyを指定する（実装済みなので省略）

　リスト11ができれば、あとはグラフを描画するコードを実行するだけです。リスト12（リスト9を再掲したもの）のコードを入力して、グラフを表示してみましょう。実行結果は既に見た図5の通りです。

import matplotlib.pyplot as plt

x, y = makedata(normdist, 0, 100, 1) # 定義域は0〜100、刻み幅は1
plt.plot(x, y)
plt.show() # 正規分布のグラフを表示

x, y = makedata(betadist, 0, 1, 0.01) # 定義域は0〜1、刻み幅は0.01
plt.plot(x, y)
plt.show() # ベータ分布のグラフを表示

リスト12　正規分布のグラフとベータ分布のグラフを描画するためのコード（再掲）
関数makedataの最初の引数に、グラフ化するデータを計算するための関数の名前（normdistやbetadist）を指定していることに注目。これらが、関数makedataの仮引数funcに渡され、それぞれの関数が呼び出される。なお、plt.show()はその時点でのグラフを描画するための関数。これを書かないと2つのグラフが同じ場所に重なって描画されてしまう。

4. 可変個の引数を使って、関数の係数や定数項を自由に指定する

　上で見た方法では、正規分布のμやσの値、ベータ分布のαやβの値は決め打ちするしかありませんでした。もっと汎用的に使えるようにするには、それらの値も引数として与えたいですね。そのために可変個の名前付き引数を使いましょう。「可変個」とは、文字通り、個数を変えることができるということです。詳細については、Python入門の記事を参照していただくこととして、ここでは、可変個の名前付き引数を使うためのコードと簡単な説明だけを書いておきます。

　まず、呼び出される関数の定義です。正規分布のμやσの値、ベータ分布のαやβの値も引数として与えるようにするので、リスト13のように書きます。

import numpy as np
from math import gamma

def normdist(x, mu=0, sigma=1): # muとsigmaを仮引数にする（既定値は0と1）
  return 1 / (np.sqrt(2*np.pi) * sigma) * np.exp(-(x-mu)**2 / (2*sigma**2)) 

def beta(a, b): # ベータ関数の定義
  return gamma(a)*gamma(b) / (gamma(a+b))

def betadist(x, a, b): # aとbを仮引数にする（指定されていないとエラーになる）
  return (x**(a-1) * (1-x)**(b-1)) / beta(a, b)

リスト13　関数の係数や定数項などを引数で指定できるようにする
関数normdistの定義にあるmu=0やsigma=1は引数の既定値の設定。muやsigmaが指定されていない場合は、それぞれ0と1が指定されたものと見なされる。関数betadistではaやbの既定値が設定されていないので、これらの引数を指定せずに呼び出すとエラーになる。

　呼び出される方の関数にはそれほど大きな変更はありませんでしたね。決め打ちにしていた値も引数で指定できるようにしただけです。

　では、呼び出す側の関数を見てみましょう。関数makedataをリスト14のように書き換えます。**argsという引数が追加されたことに注目してください。これが、可変個の名前付き引数の指定です。return文の1行上のコードを見ると、funcで参照される関数にxという配列と**argという引数がそのまま渡されることが分かります。

def makedata(func, xmin, xmax, step, **args): #  **argは可変個の引数
  x = np.arange(xmin, xmax, step)
  y = func(x, **args)
  return x, y

リスト14　可変個の名前付き引数を受け取って利用する
**引数名と指定すると、可変個の名前付き引数が指定できる。funcには、配列xと、可変個の引数**argが渡される。

　**argにはどのような値を指定すればいいのかという謎解きは少しだけ後回しにして、先に名前付き引数（キーワード引数）の意味を確認しておきましょう。名前付き引数とは仮引数名=値の形式で指定した引数のことを言います。例えば、関数betadistはbetadist(0.5, 2, 5)のように、実引数と仮引数を、指定した位置で対応させて書くこともできますが、betadist(x=0.5, a=2, b=5)のように「仮引数名=値」という形式で指定することもできます。このような方法で指定できる引数が名前付き引数です。

　では、**argの謎解きです。下のリスト15と照らし合わせながら見ていきましょう。

import matplotlib.pyplot as plt

args = {'mu': 50, 'sigma': 10}  # （1）名前付き引数のための辞書データを用意しておく
x, y = makedata(normdist, 0, 100, 1, **args) # （1）定義域は0〜100、刻み幅は1
plt.plot(x, y)
plt.show()

args = {'a': 2, 'b': 5}  # （2）名前付き引数のための辞書データを用意しておく
x, y = makedata(betadist, 0, 1, 0.01, **args) # （2）定義域は0〜1、刻み幅は0.01
plt.plot(x, y)
plt.show()

リスト15　可変個の名前付き引数に値を指定して関数を呼び出す
arg={'引数名1': 値1, '引数名2': 値2, ...}のような形式の辞書型データを用意しておき、関数の引数に**argを指定すれば、可変個の名前付き引数をまとめて渡せる。

　関数makedataを呼び出すときに**argという仮引数にどのような値を与えているのかを見てください。

• （1）arg={'mu': 50, 'sigma': 10}としておき、関数makedataに**argsを渡している
• （2）arg={'a': 2, 'b': 5}としておき、関数makedataに**argsを渡している

ということが分かります。このargという変数は辞書型という形式のデータです。（2）の例で見てみましょう。arg={'a': 2, 'b': 5}とすると、'a'というキーに対応する値が2、'b'というキーに対応する値が5であるものとして取り扱えます*5。このようにしてargに引数の名前とそれに対応する値を指定しておけば、**argsのように**を前に付けることによって、幾つかの引数をまとめて渡せるようになります（**は辞書型の引数を展開するという指定です）。この場合は、引数としてa=2, b=5が指定されたのと同じことになるというわけです。

*5　辞書型のデータでは、'a'や'b'などのキーとなる文字列や数値を使って値を取り出すことができます。上の例では、arg['a']の値は2になります。

　リスト15を見ると、関数makedataの便利さがよく分かると思います。さまざまな関数の名前と、xの定義域の最小値、最大値、増分値を指定するだけで、グラフ作成に使えるxとyの値が作成できるというわけです。

　少しばかりPythonの文法的なお話が長くなりましたが、関数の参照を引数として渡す方法や可変個の名前付き引数の利用は、便利な関数を作るのにとても役に立ちます。練習問題や次回（後編）のサンプルプログラムでもリスト14の関数makedataは大活躍します。

　さて、これまでは二次元の平面上で関数のグラフを描いてきましたが、三次元の空間でグラフを描く方法も簡単なので、紹介しておきましょう。もうひとがんばりです。

5. 3Dグラフの作成

　3Dグラフの作成も簡単です。準備としては、x, y ,zの値をそれぞれリストやNumPyの配列として用意しておくことと、subplot関数で描画領域（Axesオブジェクト）を追加し、その際にprojection='3d'と指定することだけです。グラフを描画するには、描画領域のplotメソッドを使います。以下に、数式を使って3Dのらせんを描いた例を紹介します。

　3次元のらせんは以下の式で表されます*6。cosは言わずと知れた余弦関数、sinは正弦関数です。θはラジアン単位の角度です。

*6　これまで見てきた関数は、y＝2xのように変数同士の関係が直接書かれていました。一方、上の式では、θという変数を介して関係が表されています。このような関数の表し方を「媒介変数表示」と呼びます。媒介変数表示の場合、媒介変数の値を変えるだけでxとyの値が同時に求められます（曲線のグラフを描く場合などに便利です）。

　ここでは、a＝3, b＝2として、0〜6πラジアン（0°〜1080°）までのグラフを0.1ラジアン刻みで描いてみます（リスト16、図6）。

import matplotlib.pyplot as plt
import numpy as np

a, b = 3, 2

theta = np.arange(0, 6*np.pi, 0.1) # 6πまで0.1刻みでthetaの配列を作る
x = a*np.cos(theta) # thetaの全ての要素に対するxの値を求める
y = a*np.sin(theta) # thetaの全ての要素に対するyの値を求める
z = b*theta         # thetaの全ての要素に対するzの値を求める

plt.figure(figsize=[8, 6]) # サイズを幅8インチ、高さ6インチとする
ax = plt.subplot(projection='3d')
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
ax.plot(x, y, z)
plt.show()

リスト16　3Dらせんを描くためのコード
subplot関数にprojection='3d'と指定し、描画領域（Axesオブジェクト）を追加する。ここでは、axという名前で参照できるようにした。axのplotメソッドにx, y, zの値を指定すればグラフが描画できる*7。なお、3Dであることが分かるようにplotをplot3Dと書いてもよい。Axesオブジェクトで、軸のラベルを指定するには、set_xlabel／set_ylabel／set_zlabelの各メソッドを使う。

　thetaは、np.arange関数を使って作った配列で、0〜6πまでの、0.1刻みの値になっています。x, y, zへの代入文の右辺にも注目してください。NumPyの配列に定数を掛けると、ブロードキャスト機能により、それぞれの要素に定数が掛けられた配列が返されます。これは、zの例で見ると分かりやすいでしょう。thetaは[0, 0.1, 0.2, ..., 18.8]となりますが、それにbの2という値を掛けたので、zの値は[0, 0.2, 0.4, ..., 37.6]となります。xやyも同様です。これで、thetaの全ての要素に対応するxの配列やyの配列が作成できます。

*7　実行環境によってはfrom mpl_toolkits.mplot3d import Axes3Dを記述しておかないとエラーになることもあるらしいとのことですが、Google Colab（matplotlib 3.2.2）とAnaconda（matplotlib 3.4.2）では機嫌よく動いています。

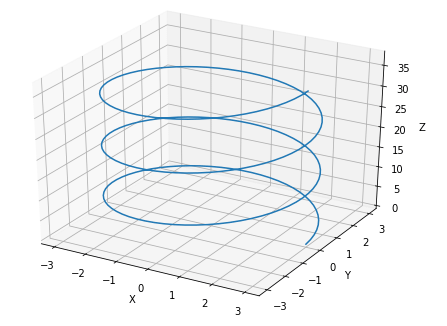図6　3Dらせんを描画した例
蛇足の細かい話だが、らせん階段のような立体的なものを「らせん（螺旋）」と呼び、蚊取り線香のような平面的なものを「渦巻き」と呼んで区別することもある。数学英語ではらせんをhelix、渦巻きをspiralと呼ぶ（が、「アルキメデスのらせん」や「対数らせん」のように平面的なものも含めて「らせん」と総称することも多い）。

　ここまで、折れ線グラフを使って関数のグラフを描く方法を見てきました。数式で表された関数がどのような形になっているのかを可視化すれば、関数として表されるモデルのイメージや性質を把握するのに役立ちます。さらに実用面を考えると、関数をグラフ化する方法だけでなく、収集したデータをグラフ化する方法についても身に付けておきたいところです。また、グラフの色などについても細かく指定したいですね。しかし、それらについては、次回（後編）で取り扱うことにします。まずは、今回の内容をしっかりと身に付けるために、練習問題に取り組んでみましょう。